Модель нейронной сети

Модель мозга

…письмоводитель градоначальника, вошедши утром с докладом в его кабинет, увидел такое зрелище: градоначальниково тело, облеченное в вицмундир, сидело за письменным столом, а перед ним, на кипе недоимочных реестров, лежала, в виде щегольского пресс-папье, совершенно пустая градоначальникова голова.

М.Е. Салтыков-Щедрин, "История одного города."

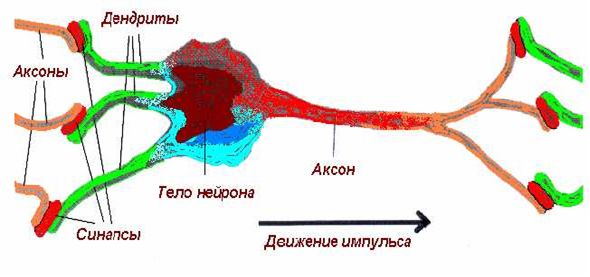
Мозг представляет собой нейронную сеть содержащую узлы — нейроны (рис.1.1) и их соединения — синапсические связи.

Рис. 1.1. Нейрон

Тело нейрона является средством выполнения пороговой функции активации над сигналами, пришедшими по входам нейрона – дендритам. (Нейрон мозга содержит до 10 тыс. дендритов.) Для того чтобы перейти в возбужденное состояние, в теле нейрона выполняются около 240 химических реакций. Величина возбуждения нейрона с помощью ветвящегося аксона передается на дендриты других нейронов.

Важными управляющими элементами связей нейронов являются синапсы. Синапс аналогичен переменному сопротивлению, определяющему вес связи (вес дендрита). Этот вес является коэффициентом, с которым дендрит принимает возбуждение нейрона, связанного с данным. Поэтому связи между нейронами называются синапсическими.

Изменение весов синапсических связей позволяет регулировать направления и пути распространения возбуждений в нейронной сети , т.е. в множестве взаимосвязанных нейронов. Так в этой сети образуются связи вида "если ... то".

Поэтому настройка весов синапсических связей является основной задачей обучения нейронной сети , когда возбуждение некоторого множества нейронов обязательно должно приводить к возбуждению определенного нейрона. Это важнейший элемент выполнения мозгом функций распознавания, управления и принятия решений.

Рис. 1.2. Модель нейрона

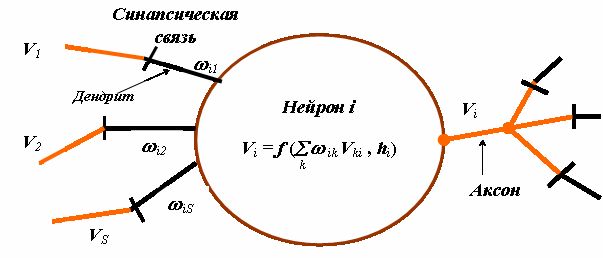
Математическая, абстрактная, модель нейрона во взаимодействии с другими нейронами сети представлена на рис.1.2.

Здесь 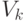— импульсы возбуждения, выработанные другими нейронами и поступившие на дендриты нейрона — веса дендритов, — пороги. В свою очередь, выработанный импульс 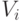также направляется на дендриты нейронов, с которыми связан нейрон с помощью ветвящегося аксона. Значение импульса возбуждения 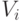находится, как говорилось ранее, в результате счета функции активации, возможный вид которой приведен на рисунке.

Еще раз обращаем внимание на то, что значения весов синапсических связей 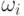и значения порогов могут регулироваться. Такое регулирование, во многих вариантах реализованное в разных моделях, и определяет возможность обучения и самообучения сети. Оно задает направление распространения возбуждений через сеть, простейшим образом формируя связи "посылка — следствие".

Нейронная сеть

На рис.1.3 показан фрагмент нейросети, по которому мы можем представить следующее.

Рис. 1.3. Фрагмент нейронной сети

1. В сети распознают входной (рецепторный) слой , воспринимающий сигналы внешнего возбуждения (например, экран, на который подается видеоизображение), и выходной слой, определяющий результат решения задачи распознавания или принятия решений. Работа сети тактируется для имитации прохождения по ней возбуждения и управления им.
2. Каждый нейрон обрабатывает сигнальную информацию (это важнейший принцип логической нейронной сети!) в диапазоне от нуля до условной единицы. Исходные данные в виде сигналов поступают (от пользователя, от блока обработки ситуации на входе, от другой нейронной сети и т.д.) или формируются (например, с помощью видео ввода) на рецепторном слое.
3. Функции активации бывают различны, но просты по объему вычислений. В простейшем случае такая функция совпадает с линейной формой, где аргументы, показанные на рис.1.2, связаны операцией вычитания. Часто удобно не вычитать порог, а только лишь сравнивать с ним указанную сумму. Другие, не менее простые, функции активации будут рассмотрены в соответствии с целесообразным их применением.
4. Найденная взвешенная сумма, превысившая порог, или величина превышения порога является величиной возбуждения нейрона либо определяет значение величины возбуждения (например, в некоторых моделях величина возбуждения всегда равна единице, отсутствие возбуждения соответствует нулю). В некоторых моделях допускают и отрицательную величину возбуждения. Значение возбуждения передается через ветвящийся аксон в соответствии со связями данного нейрона с другими нейронами.
5. По дендритам может передаваться как возбуждающее, так и тормозящее воздействие. Первое может соответствовать положительному значению веса синапсической связи , второе — отрицательному. В нейронной сети возможны обратные связи.
6. Нейронная сеть работает в двух режимах: в режиме обучения и в режиме распознавания (рабочем режиме).

В режиме обучения на рецепторном слое сети предъявляются эталоны. Веса связей на пути прохождения возбуждения формируют таким образом, чтобы на выходном слое максимально возбудился нейрон, с которым связано решение по данному эталону. Например, если показан эталон буквы А, то (по прошествии нескольких тактов, в течение которых промежуточные нейроны считают значения функции активации и передают результаты далее в соответствии со своими связями) максимально должен возбудиться нейрон, связанный с решением: "Это буква А". В рабочем режиме (в режиме распознавания), в результате показа буквы А, даже искаженной и "зашумленной", должен максимально возбудиться соответствующий нейрон выходного слоя. Так достигается эффект ассоциативного мышления.

Таким образом, "подкручивая" веса, мы учим сеть по эталонным ситуациям, по которым мы знаем решение, а затем в рабочем режиме она выдает нам решение во всем диапазоне ситуаций. При этом она автоматически решает проблему, на какую "знакомую" ей ситуацию похожа более всего предъявленная ситуация, и, следовательно, какое решение следует выдать. Конечно, — с определенной вероятностью правильности.

Это открывает широкие возможности "живого" моделирования, не только в сфере развлечений, как показано на рисунках 1.4 и 1.5, но и в сфере интеллектуального отображения. Например, "реагирующие объекты" могут своим поведением указывать на нарушение технологического процесса, на перегрузку коммуникационной сети, предвещать стихийные бедствия и т.д.

Однако то, что изображено на рис.1.3, больше соответствует воплощению в природе – в мозге. Искусственные нейронные сети значительно проще. Они сводятся к однослойным, где сигналы с рецепторов сразу обрабатываются нейронами единственного слоя, являющегося выходным. Да и формирование весов, в природе связанное со сложными биохимическими процессами, на логическом уровне реализуется исключительно просто. Как это происходит, мы рассмотрим далее на примерах построения систем принятия решений.

увеличить изображение
Рис. 1.4. Реакция на угрозу

увеличить изображение
Рис. 1.5. Реакция на поощрение