Основы трехмерного "живого" моделирования

Создание стереоэффекта с помощью системы прозрачных мониторов

Проектирование объемного изображения на плоский экран для визуализации осуществляется "на всю толщину" изображения, то есть на весь диапазон изменения , . А что если "нарезать" отображаемый объект или все пространство по оси z, направленной на зрителя, на слои "толщиной" 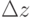(рис.12.4), и каждый такой слой проектировать на свой "передний" срез, как на отдельный экран, а экраны расположить друг за другом, как показано на рис.12.5? Ведь прозрачные мониторы уже поступили в продажу!

Рис. 12.4. "Нарезка" изображения на экранизируемые слои

Конечно, на рисунке наблюдается весьма слабый стереоэффект.

увеличить изображение
Рис. 12.5. Отображение объемного изображения на нескольких прозрачных мониторах

Изображения на разных экранах, в зависимости от угла наблюдения, оказываются смещенными относительно общей требуемой картины: с одной стороны образуются пустые зазоры, с другой изображения наползают друг на друга. Для получения стереоэффекта зрителю необходимо находиться строго напротив экранов, как показано на рисунке.

А если потребовать условного выполнения требования 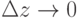? Технически и технологически это требует значительного роста количества используемых прозрачных экранов на основе достижений "прозрачной электроники". Становится оправданной разработка экранных пленок с предельной толщиной "в одну точку", чтобы "нарезка" выродилась в представление множества срезов. Собранные (склеенные) на их основе пакеты должны представлять объемное (трехмерное) экранное пространство.

В многочисленных сообщениях о достижениях в области "прозрачной электроники" пока нет ссылок на исчерпывающие научные публикации. Следует привести лишь факт результативности проводимых исследований.

Прямоугольное экранное пространство

Современные плоские экраны используются с весьма ограниченным ракурсом. Поэтому мы и размещаем телевизор где-то в сторонке, в углу. Возможно, что и столь дорогое кубическое или прямоугольное экранное пространство обречено на ограниченный угол обзора для создания должного впечатления. В этом случае прямоугольный трехмерный экран также достоин размещения где-то в углу помещения (рис.12.6).

увеличить изображение
Рис. 12.6. Прямоугольный трехмерный экран

Следует отметить, что экранное пространство образует некоторую среду, в которой действуют законы оптики. Например, не оказывается ли демонстрируемый объект погруженным в сосуд с жидкостью, подобно рыбке в аквариуме?

Более того, возможно, что взгляд сбоку, со стороны торцов экранных пленок, может встретиться с эффектом существенного отличия изображения от получаемого при взгляде спереди.

Это также может ограничить применение экрана на основе пакета плоских пленок. Однако его применение может быть вполне оправдано и даже целесообразно в случае создания реагирующего объекта для интеллектуального отображения производственного процесса, предсказания погоды или социального напряжения, для сценических постановок.