|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Нейросетевые самообучающиеся и адаптивные системы управления
Динамический выбор оптимальной стратегии распараллеливания в многопроцессорной вычислительной системе
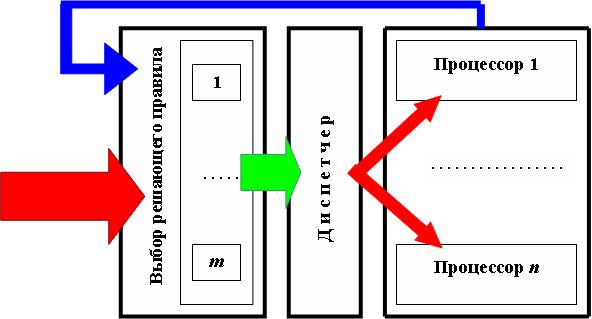
Рассмотрим обобщенную адаптивную схему динамического оптимизированного распределения потока задач между процессорами в многопроцессорной вычислительной системе или в сегменте вычислительной сети (рис.6.5). Такая обработка характерна для Центра GRID-технологий. Критерием оптимизации является достижение максимальной загрузки процессоров или выделенных сетевых ресурсов, служащей максимальной пропускной способности используемых вычислительных средств [9]. В основе диспетчера, распределяющего поток запросов на решение задач, лежат несколько эвристических решающих правил , каждое из которых реализует некоторую стратегию распараллеливания. Решающие правила различаются по скорости реализации и по достигаемому эффекту в части статистических оценок обеспечения высокой пропускной способности. Выбор решающего правила и локализация его применения во времени зависят от характеристик потока запросов: от переменной плотности, от их типового состава, приоритета задач, частичной упорядоченности.
Организация динамического распараллеливания вычислений – диспетчирование является основным трудоемким и ответственным элементом построения управляемого вычислительного процесса в многопроцессорных вычислительных системах и вычислительных комплексах на основе сегментов ЛВС.
В этом случае задача диспетчирования становится трудно формализуемой. Оперативное управление текущим выбором стратегии необходимо производить с помощью логической нейронной сети, на рецепторный слой которой подаются текущие и пролонгированные характеристики потока запросов, а также текущие параметры состояния системы обслуживания. Нейроны выходного слоя максимальным возбуждением указывают на решающее правило , которым следует пользоваться в дальнейшем. То есть, максимально возбужденный нейрон выходного слоя инициирует запуск соответствующей процедуры распределения в составе диспетчера.
Адаптация обеспечивается возможностью перезакрепления решающих правил за нейронами и вводом в рассмотрение новых правил – по статистическим оценкам эффективности распределения (распараллеливания).
Рассмотренная схема легко развивается, модифицируется и специализируется.
Выделение неизменного состава характеристик, участвующих в принятии каждого решения, служит основой построения простейших по структуре совершенных логических нейронных сетей, где функция активации является аналогом конъюнкции и производит суммирование значений входных сигналов. Поскольку такая нейронная сеть является однослойной, то на деле реализуется простейшая схема "голосования" в пользу той стратегии, которая в наибольшей степени адекватна сложившейся ситуации – текущим характеристикам потока запросов и состоянию системы обслуживания.
При этом основная трудность диспетчирования заключается в частичной упорядоченности (во времени выполнения) работ, которая присуща системам управления в реальном времени.
Диспетчер распараллеливания входит в состав операционной системы компьютера и сам по себе увеличивает "накладные расходы" производительности на собственную реализацию во времени. Поэтому быстродействие диспетчера представляет важнейшее требование к нему.
Другим требованием, предъявляемым к диспетчеру распараллеливания, является достаточная близость формируемых им планов к точным оптимальным, полученным на основе решения задачи распараллеливания в адекватной постановке.
Дело в том, что решаемая диспетчером задача относится к важному классу задач исследования операций [9] – к классу задач параллельного программирования. Это задачи экспоненциальной сложности (NP-сложные задачи). Решение таких задач для множеств частично упорядоченных работ весьма трудоемко и никак не может быть положено в основу программ операционной системы компьютера. Поэтому прибегают к эвристическим методам полиномиальной сложности (Р-сложность) для оперативного, динамического распараллеливания. В основе таких методов можно выделить одно или более решающих правил , погруженных в алгоритм распараллеливания и обусловленных предпочтительным выбором альтернативы в ключевых ситуациях.
Применение каждого решающего правила при распараллеливании влечет различный объем вычислений – накладных расходов. Однако, как правило, увеличение сложности алгоритмов распараллеливания обусловлено попытками приблизить результаты планирования к точным оптимальным. Поэтому, по результатам достаточного опыта, можно считать, что более трудоемкий диспетчер статистически обеспечивает планы параллельного выполнения работ, более близкие к оптимальным.
При практическом решении задач распараллеливания ограничиваются однородными системами выделяемых средств (однородными вычислительными системами [9]), а различные подходы к диспетчированию отличаются вариантами единственного решающего правила .
По трудоемкости, а, следовательно, "по оптимальности", варианты решающего правила можно упорядочить:
- Из множества работ, выполнение которых может начаться в текущий момент времени, назначение на свободные процессоры следует производить произвольно (по сложившемуся порядку номеров, первую в списке, случайно и т.д.).
- Из множества работ, выполнение которых может начаться в текущий момент времени, назначение на свободные процессоры следует производить в порядке не возрастания времени выполнения работ (в первую очередь назначать работу с максимальной оценкой времени выполнения).
- Из множества работ, выполнение которых может начаться в текущий момент времени, в первую очередь на свободный компьютер (процессор) назначать работу, предшествующую максимальному объему непосредственно или транзитивно следующих ей работ, включая ее саму.
- При известном директивном сроке выполнения комплекса работ (в том числе – в системе реального времени), из множества работ, выполнение которых может начаться в текущий момент времени, назначать на свободный компьютер (процессор) работу, обладающую минимальным значением позднего срока окончания выполнения.
- В дополнение к 4: При равных минимальных значениях позднего срока окончания выполнения в первую очередь назначить работу в соответствии с правилом 3.
В различных случаях применения эффективно используются и другие комбинации решающих правил 2, 3, 4.
Первое и второе решающие правила используются в динамических диспетчерах, предполагающих выполнение назначенных работ одновременно с дальнейшим планированием.
Третье и последующие решающие правила предполагают работу диспетчера вне времени выполнения назначенных работ: диспетчер разрабатывает план выполнения этих работ, затем этот план реализуется без включения диспетчера. Это обеспечивает плотную загрузку процессоров при выполнении работ и, следовательно, их скорейшее освобождение – переход в свободный ресурс.
Очевидно, что чем большим ресурсом времени обладает диспетчер в связи с "разреженным" потоком высокоприоритетных заданий при заданных директивных сроках выполнения, тем больше искушение использовать решающие правила для распределения этих заданий, приближающие результаты планирования к оптимальным. Ведь при этом достигается минимальное время выполнения совокупности взаимозависимых работ, плотно загружаются процессоры, выделяется время для фонового выполнения запросов с меньшим приоритетом. Это справедливо, если одновременное увеличение накладных расходов на планирование в совокупности с разработанным планом все же служит оптимизации параллельного вычислительного процесса, то есть, минимизации времени выполнения комплекса работ высокого приоритета.
С другой стороны, очевидно, что при плотном потоке заданий не высокого приоритета требование их оперативного распределения между вычислительными средствами заслоняет собой все другие требования к оптимизации вычислительного процесса. Становится не до оптимизации: ведь плотная загрузка всех средств и так гарантирована! В этом случае достаточно использовать простейшее решающее правило .
Таким образом, только на основе моделирования и опытных исследований, для достаточного числа точек факторного пространства – характеристик потоков заданий, их временных характеристик, директивных сроков их выполнения, требуемых ресурсов и состояния загрузки вычислительных средств, – можно получить ряд рекомендаций по применению решающих правил в диспетчере распараллеливания.
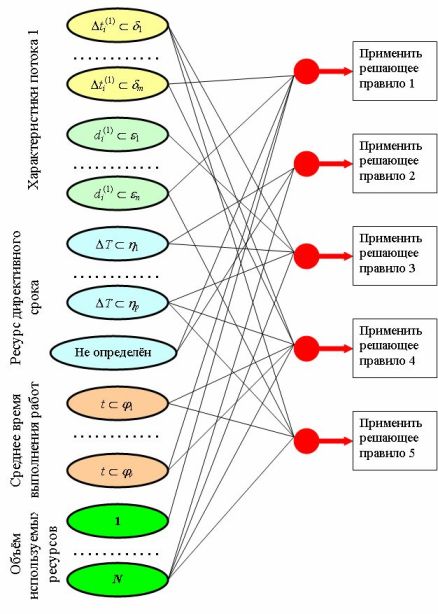
Так формируется основа логической нейронной сети, примерный вид которой приведен на рис.6.6. Связи устанавливаются на основе моделирования или опытных данных. Предполагается, что обслуживается высокоприоритетный поток задач оперативного планирования и управления (например, в системе реального времени), для которого резервирование вычислительных средств производится заранее с помощью диспетчера ресурсов.
Директивный срок Т определяется, как длина отрезка времени, через которое распределяемое множество частично упорядоченных работ должно быть выполнено обязательно. Ресурс директивного срока при планировании распараллеливания определяется как разность,
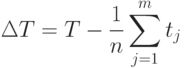
где  – число выделенных процессоров,
– число выделенных процессоров,
 – количество распределяемых работ.
– количество распределяемых работ.
На рисунке:
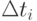 – усредненное по серии последних запросов время между запросами;
– усредненное по серии последних запросов время между запросами;
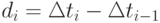 – аналог первой производной.
– аналог первой производной.
Таким образом, на рецепторном слое указывается принадлежность характеристик интервалам значений или значениям. Максимальное возбуждение нейрона выходного слоя (при высоком пороге) указывает на необходимость автоматического включения соответствующего решающего правила в диспетчер.
Возможность оптимизации совместной реализации запросов на выполнение нескольких частично упорядоченных работ предполагает частичное или полное накопление этих запросов (работ) в некотором "окне просмотра" диспетчера. Диспетчер с высокой частотой анализирует содержимое "окна просмотра", пытаясь "уложить" выполнение этих работ за минимальное время, не превышающее директивный срок Т. Время выполнения запросов, а также время работы диспетчера, измеряется условными единицами. Временные оценки известны заранее.
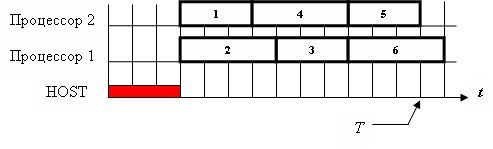
Пусть для выполнения работ выделены два процессора суперкомпьютера. Диспетчер реализован на управляющем процессоре – на HOST-процессоре.
В "окне просмотра" накопились работы, частичную упорядоченность (порядок следования) которых можно описать информационным графом (рис.6.7).
Пусть диспетчер использует решающее правило 1. Время его однократного выполнения составляет 1 у.е., Т = 13 у.е.
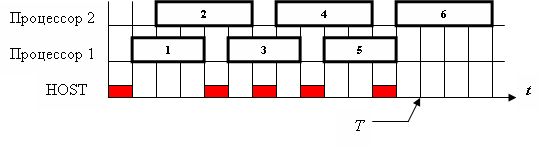
Тогда временная диаграмма выполнения комплекса работ представлена на рис.6.8.
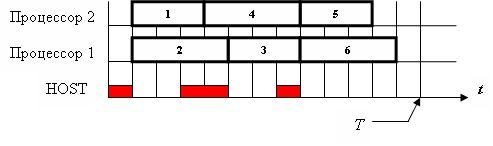
Для диспетчера, использующего решающее правило 2, временная диаграмма выполнения того же комплекса работ на двух процессорах представлена на рис.6.9.
Временная диаграмма выполнения того же комплекса взаимосвязанных работ для диспетчера, реализующего решающее правило 4, при заданном директивном сроке окончания выполнения Т = 13 у.е., представлена на рис.6.10. Учтено, что время однократной работы диспетчера для двух выделенных процессоров составляет 3 у.е.
На основе результатов применения решающих правил 1, 2 и 4 в диспетчере можно сформулировать гипотезу экспертной рекомендации для записи связей (трассировки) в логической нейронной сети на рис.6.6. Для этого необходимо найти среднее время t выполнения работы, интенсивность потока запросов на отрезке [0, T] и ресурс директивного срока 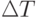 . Интенсивность потока в примере принимается постоянной.
. Интенсивность потока в примере принимается постоянной.
Такая гипотеза может быть следующей:
Для ![t\subset[3, 4], \Delta T \subset [2, 4], \Delta t_{i(1)} \subset [0,4, 0,5], d_{i(1)} \subset [0, 0,001]](/sites/default/files/tex_cache/0e363c4e59f3cff00cc983957b9364a1.png) , и для двух процессоров следует считать предпочтительным применение в диспетчере решающего правила 2.
, и для двух процессоров следует считать предпочтительным применение в диспетчере решающего правила 2.
Ключевые термины
"Бесформульные" вычисления – вычисления, совершаемые не на основе счета значений арифметических выражений, а на основе ассоциативной выборки из базы знаний с возможностью усреднения близких результатов выборки.
Самообучение – производится в результате пополнения базы знаний новыми отношениями вида "если – то", получаемыми из опыта.
Ситуационное управление – управление объектами или сложными системами с помощью условных таблиц, в строках которых указаны вектора возможных ситуаций и соответствующие им вектора значений необходимых воздействий.
Решающее правило – основное правило действий, лежащее в основе эвристического алгоритма оперативного планирования, предпринимаемое в случае не единственной альтернативы выбора решения на локальном уровне.
Краткие итоги
- Может показаться, что предлагаемый здесь способ "бесформульных" вычислений представляет собой лишь сложную интерпретацию табличного метода. Однако применение логических нейронных сетей позволяет осуществить
- Переход к нечетким, то есть к недостоверным данным;
- Совместное использование данных и объектов разных типов и свойств (хотя в лекции приводится пример числовых данных при использовании в векторных функциях от векторных переменных, для описания конкретных зависимостей в реальной исследуемой области предложенные рекомендации могут быть легко расширены);
- Выполнение интерполяции (экстраполяции) на основе нахождения среднего, допускающей рассмотрение большого числа решений, на которые указывают нейроны, возбуждение которых превысило порог;
- Любое увеличение длины исследуемых векторов без существенного влияния на вычислительную нагрузку. При увеличении размерности задачи возрастает лишь объем базы знаний;
- Схема ситуационного управления легко трансформируется в схему "бесформульных" вычислений. Включение в нее точной модели управляемого процесса (при невозможности натурных экспериментов) позволяет получить самообучающуюся систему управления. Нейросетевое воплощение обеспечивает малую сложность алгоритмов управления и высокую реальную производительность вычислительных средств в рабочем режиме.
- Не ищите способы непосредственного получения расписания использования ресурсов методами, позволяющими производить лишь оценки. Расписания, в том числе оптимальные, получаются лишь при численном решении задач планирования. Выбор решающих правил, лежащих в основе приближенных, эвристических алгоритмов планирования, может производиться динамически на основе оценки складывающейся обстановки и ее прогнозирования. Логическая нейронная сеть при этом способна быть хорошим помощником.
Вопросы:
- На чем основана идея "бесформульных" вычислений и как она реализуется с помощью логической нейронной сети?
- Как осуществляется ситуационное управление?
- Как идеи ситуационного управления развиваются для построения самообучающихся систем управления?
- Как реализуется самообучающаяся система управления с помощью логической нейронной сети?
- В чем заключается способ учета текущих и прогнозируемых характеристик потока запросов при выборе оптимального плана их параллельного (многоканального) обслуживания?
- Как производится настройка (адаптация) диспетчера оптимального распараллеливания по текущим и прогнозируемым характеристикам потока запросов?
Дополнительные материалы к лекции, Вы можете скачать ![]() здесь.
здесь.