|
"Тогда как задать возбуждение рецепторов, если инспектор точно установил, что скорость автомобиля при наезде на пешехода была равна 114 км/час? Вопрос по расчёту скорости и сумме достоверности: этот математический (приведенный выше в виде контекста из материала лекции 1, страницы 3) метод справедлив к скоростным показателям выходящим за рамки диапазона 100-120. |
Развитие логической нейронной сети для распознавания объектов по заданному набору признаков
Структурированная, не однослойная логическая нейронная сеть
Маша готова к компромиссу. Ее представления о идеальном мужчине расширяются. В качестве желанного жениха она готова рассмотреть не менее шикарный вариант 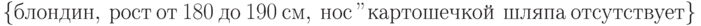 .
.
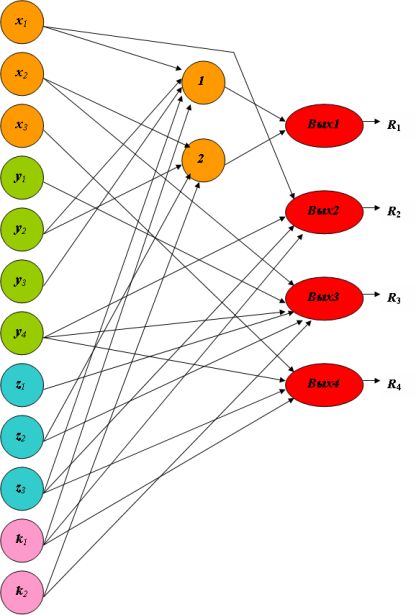
Казалось бы, достаточно дополнить нейронную сеть на рис.5.1 связями, ведущими из рецепторов, соответствующих указанным параметрам, к нейрону Вых1, указывающему на решение  . Однако это не так. При попытке ограничиться одним слоем необходимо проверить, не поглотил ли обобщенный эталон, предполагающий некоторое решение, другой обобщенный эталон, ведущий к другому решению. Следовательно, может случиться, что для некоторых ситуаций возможно неоднозначное решение.
. Однако это не так. При попытке ограничиться одним слоем необходимо проверить, не поглотил ли обобщенный эталон, предполагающий некоторое решение, другой обобщенный эталон, ведущий к другому решению. Следовательно, может случиться, что для некоторых ситуаций возможно неоднозначное решение.
В данном случае, при выбранном множестве решений, такая опасность пока отсутствует. Однако при расширении системы принятия решений, то есть при формировании новых решений по некоторым, пока не рассмотренным ситуациям, возможна неоднозначность рекомендуемых решений. Например, Маша скоро захочет сформировать новое решение  на основе логического выражения
на основе логического выражения
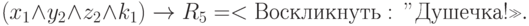
Легко видеть, что при непосредственном связывании рецепторов с нейронами выходного слоя в однослойной сети задание (единицами) указанной ситуации приведет к активизации двух решений – 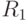 и
и 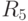 .
.
Известны два способа ликвидации неоднозначности решений.
Первый способ заключается в строгом воспроизведении структуры нового логического выражения, определяющего решение R1:
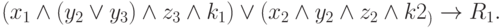 |
( 5.2) |
Наличие скобок указывает на структуризацию формируемой сети (рис.5.3); она становится не однослойной. Тогда целесообразно использовать рассмотренную функцию активации с высоким значением порога. Важность использования высокого порога обусловлена тем, что при замене логических операций дизъюнкции и конъюнкции операцией суммирования входных сигналов нейроподобного элемента при возникновении соответствующей ситуации должен возбудиться лишь один из нейронов - №1 или №2.
В противном случае величины возбуждения этих нейронов будут складываться при формировании возбуждения нейрона Вых1. При этом значение возбуждения нейрона 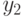 будет учтено дважды. Тогда нейроны выходного слоя будут обладать неодинаковыми величинами максимально высокого возбуждения, что снизит достоверность выводов нейронной сети.
будет учтено дважды. Тогда нейроны выходного слоя будут обладать неодинаковыми величинами максимально высокого возбуждения, что снизит достоверность выводов нейронной сети.
Преобразование структурированной нейросети в однослойную, допускающую неограниченное развитие
Второй способ ликвидации неоднозначности принимаемых решений называется размножением решений. Он заключается в том, что каждая конъюнкция в выражении вида (5.2) приводит к возбуждению одного нейрона выходного слоя. То есть, каждый нейрон, выполняющий роль конъюнктора, инициирует одно и то же решение, которое закреплено за разными нейронами.
В этом случае можно записать два логических выражения, обусловливающих решение 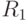 : заданное первоначально и новое
: заданное первоначально и новое
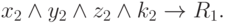
Появившаяся интерпретация того же решения вводит в искушение развития системы принятия решений. Например, первое вхождение 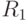 в описание системы может быть дополнено разъяснением:
в описание системы может быть дополнено разъяснением:

Второе вхождение 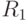 может привести к аналогичному изменению:
может привести к аналогичному изменению:
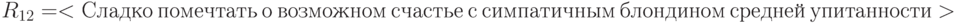
Таким образом, принимаемые решения в действительности отличаются одно от другого, а нейронная сеть остается однослойной. Это облегчает ее обработку.
увеличить изображение
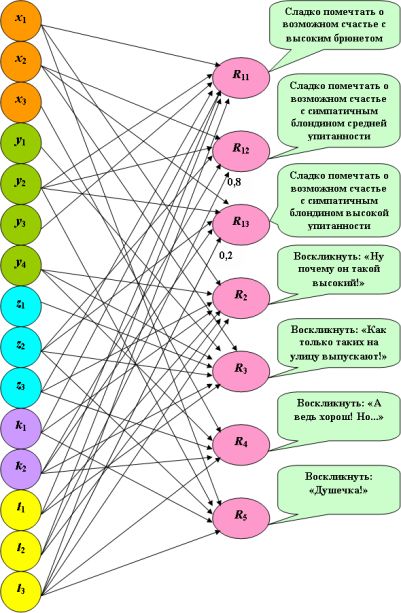
Рис. 5.4. Развитие однослойной логической нейронной сети с функцией активации (5.1)
И тут Машу впервые посещает мысль о действенности такого важного свойства – признака мужчины, как упитанность (рис.5.4; отражено решение 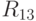 для признака высокой упитанности; веса, равные единице, не отмечены).
для признака высокой упитанности; веса, равные единице, не отмечены).
Создавая исчерпывающее множество событий, Маша полагает, что упитанность бывает низкой, средней и высокой.
Следовательно, необходимо входной слой дополнить тремя рецепторами 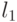 ,
, 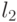 и
и 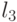 . Влияние нового фактора на принятие решений неодинаково. Так, ситуация <высокий брюнет с длинным носом, да еще и в шляпе>, приводящая к решению
. Влияние нового фактора на принятие решений неодинаково. Так, ситуация <высокий брюнет с длинным носом, да еще и в шляпе>, приводящая к решению 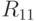 , подавляет фактор упитанности, исключает какую-либо зависимость от нее. Поэтому к решению
, подавляет фактор упитанности, исключает какую-либо зависимость от нее. Поэтому к решению 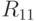 должны вести связи от всех рецепторов, ведающих упитанностью.
должны вести связи от всех рецепторов, ведающих упитанностью.
Ситуация, приводящая к решению  , как говорилось ранее, напрямую учитывает фактор упитанности, но не так что уж полностью. Подумав, Маша решает учитывать среднюю упитанность с весом 0,8, а высокую – с весом 0,2. Решение
, как говорилось ранее, напрямую учитывает фактор упитанности, но не так что уж полностью. Подумав, Маша решает учитывать среднюю упитанность с весом 0,8, а высокую – с весом 0,2. Решение 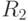 она не ставит в зависимость от упитанности. Поэтому, как и к решению
она не ставит в зависимость от упитанности. Поэтому, как и к решению 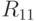 , к решению
, к решению 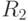 должны вести связи от рецепторов
должны вести связи от рецепторов 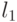 ,
, 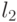 и
и 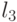 . Решение
. Решение 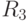 зависит от низкой упитанности с весом единица. Вес высокой упитанности при принятии решений
зависит от низкой упитанности с весом единица. Вес высокой упитанности при принятии решений  и
и 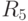 также принимается равным единице.
также принимается равным единице.
Поясним необходимость введения связей от рецепторов 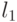 ,
, 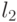 и
и 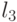 к нейронам, определяющим решения
к нейронам, определяющим решения 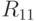 и
и 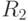 . Ведь это может запутать разработчика СПР.
. Ведь это может запутать разработчика СПР.
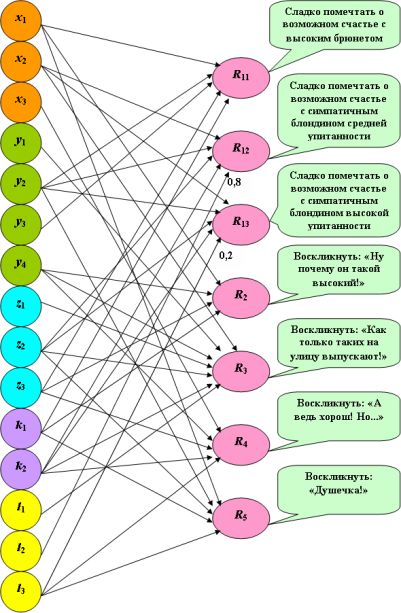
Неодинаковое отображение всех исчерпывающих множеств событий на нейронах выходного слоя (рис.5.5; указанные связи исключены), а также введение весов связей, отличных от единицы, приводят к тому, что при использовании функции активации (5.1) исследуемые ситуации, определяемые комбинациями единиц на рецепторном слое, приводят к неодинаковому максимальному возбуждению нейронов выходного слоя.
увеличить изображение
Рис. 5.5. Развитие однослойной логической нейронной сети с функцией активации (5.3)
Так, комбинация 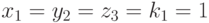 приводит к равному 4 значению возбуждения нейрона выходного слоя, соответствующего решению
приводит к равному 4 значению возбуждения нейрона выходного слоя, соответствующего решению 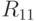 .
.
Комбинация  приводит к значению возбуждения, равному 4,8, на выходе, соответствующем решению
приводит к значению возбуждения, равному 4,8, на выходе, соответствующем решению  . Это приводит к необходимости приведения величины возбуждения нейронов к одному диапазону изменения - делением на максимальную величину их возбуждения. Такого же эффекта можно добиться корректировкой передаточной функции.
. Это приводит к необходимости приведения величины возбуждения нейронов к одному диапазону изменения - делением на максимальную величину их возбуждения. Такого же эффекта можно добиться корректировкой передаточной функции.
При корректировке функции активации необходимо учесть следующие соображения.
- Неодинаковые значения максимального возбуждения нейронов выходного слоя снижают достоверность выводов, порождают их взаимное влияние. Это особенно сказывается при переходе к рассмотрению нечетко (на основе достоверности) задаваемых значений наблюдаемых признаков.
- Целесообразно повысить степень определенности влияния важных факторов на принятие наиболее ответственных решений в ущерб второстепенным факторам. Так, при принятии решения
 средняя упитанность, учитываемая с весом 0,8, превалирует над высокой упитанностью, учитываемой всего лишь с весом 0,2. Следовательно, при корректировке параметров нейронной сети, для увеличения достоверности выводов, необходимо сделать выбор в пользу учета средней упитанности, невзирая на возможность дальнейшего подавления учета упитанности высокой.
средняя упитанность, учитываемая с весом 0,8, превалирует над высокой упитанностью, учитываемой всего лишь с весом 0,2. Следовательно, при корректировке параметров нейронной сети, для увеличения достоверности выводов, необходимо сделать выбор в пользу учета средней упитанности, невзирая на возможность дальнейшего подавления учета упитанности высокой. - Необходимо позаботиться о том, что в будущем разрабатываемая нейронная сеть, возможно, образует лишь звено в длинной логической цепочке выводов в процессе общественной или хозяйственной деятельности Маши. Это означает, что выходной слой данной нейронной сети должен быть готов к превращению в рецепторный слой следующей нейронной сети для продолжения дедуктивной логической цепочки умозаключений. Например, в перспективе своей деятельности Маша наметила получить общественный социально-политический срез на основе функции алкогольной зависимости мужского населения родного города. Следовательно, значения возбуждения нейронов выходного слоя не должны превосходить единицы.
На основе этих соображений целесообразно выбрать следующую функцию активации:
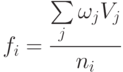
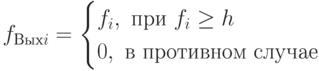 |
( 5.3) |
Здесь 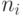 – длина конъюнкции на входе нейрона. Она равна максимальному количеству активных входов i-го нейрона выходного слоя, участвующих в формировании конъюнкций, входящих в состав соответствующего логического выражения. Так (рис.5.5), для нейрона, определяющего решение
– длина конъюнкции на входе нейрона. Она равна максимальному количеству активных входов i-го нейрона выходного слоя, участвующих в формировании конъюнкций, входящих в состав соответствующего логического выражения. Так (рис.5.5), для нейрона, определяющего решение 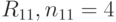 ; для нейрона, определяющего решение
; для нейрона, определяющего решение 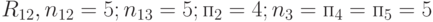 .
.
В Лекции 13 предложена более точная функция активации, предполагающая применение в знаменателе выражения (5.3) суммы весов  . Тогда функция активации принимает вид:
. Тогда функция активации принимает вид:
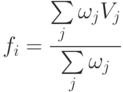
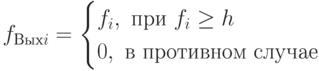 |
( 5.4) |
Однако не столь скрупулезное уточнение величины возбуждения нейронов выходного слоя, исключающее столь глубокий, проведенный выше, анализ, демонстрирует достаточность, при формировании возбуждения нейронов, учета всех рецепторов, соответствующих тем исчерпывающим множествам событий, от которых эти нейроны не зависят. Этим, по крайней мере, будет достигнут тот результат, что длина всех конъюнкций будет одинакова. Таким образом, нейронная сеть на рис.5.4 с функцией активации (5.1) вполне работоспособна, если не используется в длинных логических цепочках.