Обучение логической нейронной сети

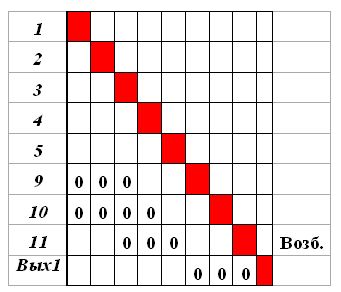
Вновь выделяем столбцы, соответствующие "возбужденным" входам матрицы. Это столбцы, соответствующие нейронам В1, А1, 6. Находим строку в выделенной совокупности столбцов, имеющую максимальное число "нулей". Такая строка соответствует нейрону 11. Заменяем в этой строке (в выделенной совокупности столбцов) "нули" "единицами", т.е. максимально увеличиваем веса. Присваиваем нейрону 11 признак "возбужден" и значение 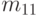= 3. Отражаем изменение весов в матрице S.

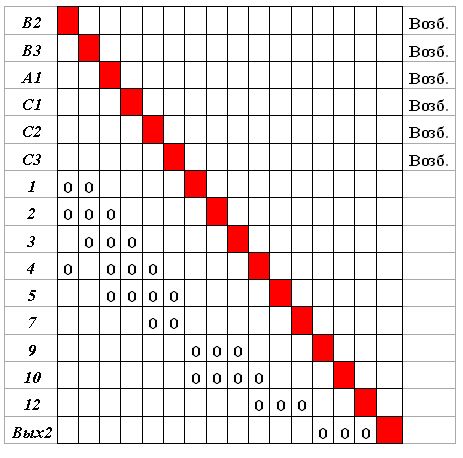
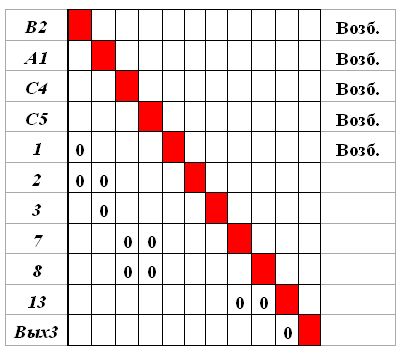
Исключаем из матрицы строки и столбцы, соответствующие нейронам В1, А1, 6. Матрица принимает вид, изображенный на рис.4.11.

Рис. 4.11. Второй шаг преобразования матрицы следования S1

Исключаем из матрицы все входы, которые соответствуют нейронам 1, 2, 3, 4, 5, не обладающим признаком "возбужден". Ведь строящийся нами путь возбуждения уже миновал эти нейроны! Исключение этих нейронов породит новые нейроны, нуждающиеся в исключении по той же причине, — нейроны 9 и 10.

(Последовательное исключение сверху вниз динамически учитывает появление таких нейронов и гарантирует полное исключение за один проход.) Матрица примет вид на рис.4.12.

Рис. 4.12. Последний шаг преобразования матрицы следования S1

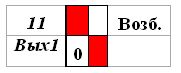
Теперь в первом столбце имеется единственная строка с "нулем" — соответствующая нейрону Вых1. Меняем "нуль" на "единицу" — получаем окончательный возможный путь возбуждения по заданному эталону. Изменения отражаем в матрице S.

Рис. 4.13. Нейросеть, обученная первому эталону

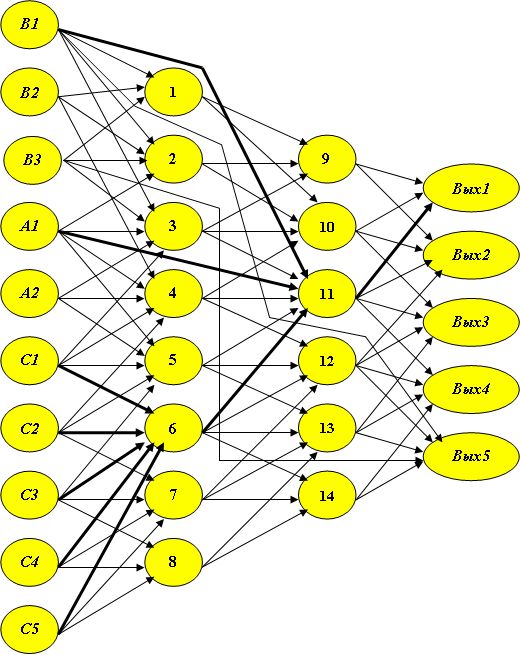
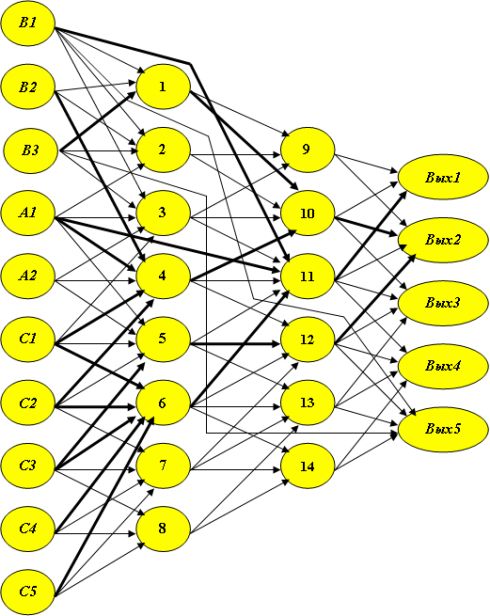
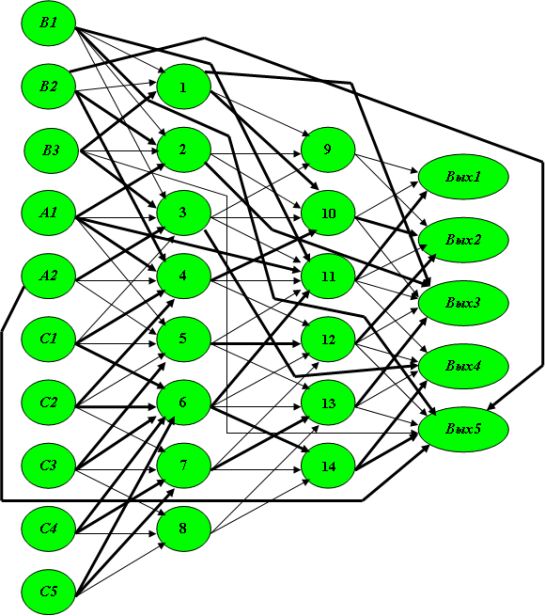
Мы не будем приводить новый вид матрицы следования S, а на изображении самой сети (рис.4.13) выделим темным построенную трассу.

Реакции на один обобщенный эталон мы сеть научили.

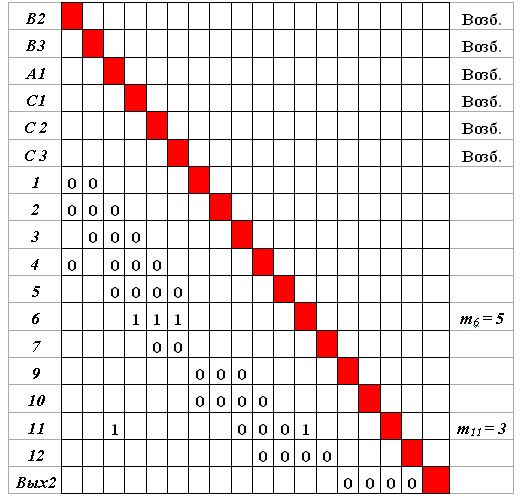
По сети на рис.4.13 или по матрице на рис.4.8 (с учетом частичного обучения!) построим (рис.4.14) матрицу статического пути возбуждения 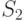[B2, B3, A1, C1, C2, C3 Вых2].

Рис. 4.14. Первоначальный вид матрицы следования S2 для обучения второму эталону

Нейрон 6 ранее "объединил" возбуждение пяти нейронов: С1, С2, С3, С4, С5, т.е. в матрице S в соответствующей строке содержится пять единиц и 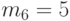. Однако в составленной матрице 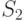в строке, соответствующей этому нейрону, присутствуют лишь три единицы. Значит, этот нейрон не может быть использован для трассировки необходимого пути возбуждения, т.к. комбинация С1&С2&С3&С4&С5 нам здесь не нужна.

То же следует сказать и о нейроне 11.

Исключим из данной матрицы строки и столбцы, соответствующие нейронам 6 и 11. Матрица примет вид, показанный на рис.4.15. Так как она не содержит единиц, то ее трассировка не привлечет новых особенностей. Результат обучения второму эталону представлен на рис.4.16.

Рис. 4.15. Матрица следования S2 для обучения второму эталону

Рис. 4.16. Нейросеть после обучения двум эталонам

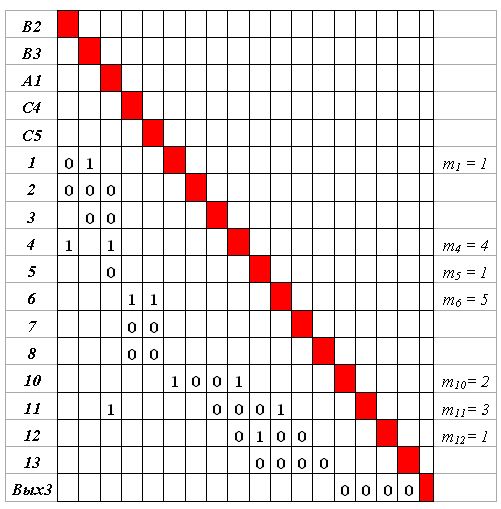
Обучим сеть третьей ситуации, требующей решения R3. Закрепим за этим решением нейрон Вых3. Матрица [B2, B3, A1, C4, C5 Вых3] представлена на рис.4.17.

Рис. 4.17. Матрица следования S3 для обучения третьему эталону (начальный вид)

Исключаем из матрицы представительство тех ранее использованных ("возбужденных") нейронов, для которых значение m (указано в дополнительном столбце матрицы) превышает количество единиц в соответствующей строке. Это значит, что эти нейроны "собрали" уже возбуждение нейронов, которые в данном пути возбуждения, т.е. в матрице , не используются. Это нейроны 4, 5, 6, 11. Переиспользование их невозможно.

Повторяем попытки исключения из матрицы представительство тех нейронов, для которых значение m стало превышать количество единиц в соответствующей строке. И так далее — до исчерпания этой возможности.

В данном случае нам придется исключить из рассмотрения (вследствие исключения нейронов 4 и 5) нейроны 10 и 12. Матрица примет окончательный вид на рис.4.18.

Рис. 4.18. Окончательный вид матрицы следования S3 для обучения третьему эталону

Присваиваем всем нейронам, образующим входы матрицы, признак "возбужден".

Выделяем и объединяем столбцы, соответствующие входам матрицы .

Отобразим новую особенность алгоритма трассировки, обусловленную наличием в матрице "единиц".

А именно, в выделенных столбцах находим строку, содержащую хотя бы одну единицу. Она (строка) представляет тот нейрон, который "собрал" (при анализе предыдущих эталонов) возбуждение одного или более нейронов, образующих входы. Эти нейроны, "передавшие" свое возбуждение, могут быть исключены из рассмотрения. Среди таких строк выбираем строку с максимальным числом единиц.

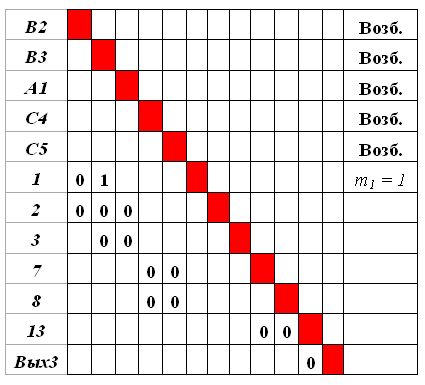
Так, нейрон 1 возбужден единственным нейроном, принадлежащим текущему множеству входов матрицы, — нейроном В3. Впредь он представляет этот нейрон, который может быть исключен из рассмотрения. Матрица принимает вид на рис.4.19.

Рис. 4.19. Первый шаг преобразования матрицы следования S3

Подтверждаем нейрону 1 признак "возбужден" и превращаем его во вход матрицы , уничтожив веса в его строке.

Вновь находим множество входов матрицы и выделяем соответствующие им столбцы. Пытаемся найти строку, содержащую единицы в этих и только этих столбцах, но таких больше нет. Тогда находим строку, содержащую максимальное число нулей. Первая такая строка соответствует нейрону 2. "Объединяем" на нем возбуждение нейронов В2 и А1, заменяя нули единицами. Полагаем m2 = 2, исключаем нейроны В2 и А1 из рассмотрения, присваиваем нейрону 2 признак "возбужден". Отражаем сделанные изменения весов в матрице S.

Рис. 4.20. Нейросеть после обучения третьему эталону

Исключаем входы, не обладающие признаком "возбужден", — нейроны 3 и 5. Продолжая процесс подобно предыдущему, получаем результат обучения трем эталонам (рис.4.20).

Окончательный вид полностью обученной нейронной сети представлен на рис.4.21, где, напоминаем, веса, принявшие значение 1, в том числе введенные дополнительно, соответствуют жирным стрелкам.

Рис. 4.21. Обученная нейросеть

Ключевые термины

1. Обучение нейронной сети – фиксирование причинно-следственных связей между ситуациями и следующими им решениями с помощью значений синапсических весов. Связи находятся так, чтобы при "единичном" возбуждении рецепторов, отражающих ситуацию, максимально возбуждался нейрон выходного слоя, указывающий на принимаемое решение.
2. Обобщенный эталон – множество значений исходных факторов, возможно, отражающих не единственную ситуацию, приводящих к одному решению. Формируется для каждой отдельной логической функции описания системы принятия решений.
3. Трассировка нейронной сети – обучение с помощью формирования трасс: совокупности путей, ведущих от рецепторов, определяющих обобщенный эталон, к нейрону выходного слоя, соответствующего решению. Трасса отмечается "единичными" весами использованных в ней связей.
4. Матрица следования – отображает матричное описание логической нейронной сети. Представляет удобный аппарат формальных преобразований для трассировки и расчетов.
5. Транзитивные связи – отражают не непосредственные связи между нейронами, а их совместное участие в некоторой логической цепочке.
6. Дистрибутивное преобразование – приведение логической функции к виду "дизъюнкции конъюнкций", то есть, к такому виду, при котором отдельные высказывания о значениях факторов объединены операцией И (в конъюнкции), а несколько таких конъюнкций объединены операцией ИЛИ (дизъюнкцией). Такое преобразование в основном использует известное из булевой алгебры свойство дистрибутивности конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции.
7. Размножение решений – постановка каждой "конъюнкции", образованной в результате дистрибутивного преобразования, того решения, которое соответствует значению ИСТИНА всего логического выражения.
8. Статический путь возбуждения – множество всех путей в графе, ведущих от выделенного множества входных вершин в некоторую выходную вершину.

Краткие итоги

1. Построение нейронной сети на основе достоверности высказываний о принадлежности данных значительно упрощает традиционный подход к нахождению значений синапсических весов при обучении нейронной сети без обратных связей и сводится к нетрудоемкой трассировке.
2. Обучение происходит в результате нахождения путей в исходном графе, описывающем связи между нейронами. Эти пути ведут от рецепторов, определяющих каждую ситуацию или образующих обобщенный эталон, к нейрону выходного слоя, указывающему на соответствующее решение. Дуги (связи), образующие путь, метятся максимальными (единичными) весами.
3. Алгоритм трассировки допускает неоднократное использование нейронов при отображении термов – общих логических конструкций в составе более чем одной логической функции, составляющей описание системы принятия решений. Таким образом, осуществляется "экономное" расходование нейронов сети.
4. Алгоритм трассировки допускает развитие структуры заданного графа в том случае, если связей в нем оказывается недостаточно. Необходимые связи вводятся автоматически.

Вопросы:

1. Когда возникает проблема обучения логической нейронной сети и в чем ее идея?
2. Как (на иллюстративном уровне) производится обучение нейронной сети заданной структуры распознаванию символов с помощью эталонных "ловушек"?
3. Как описание структуры логической нейронной сети с помощью матрицы следования способствует формальному решению задачи обучения?
4. Вводятся ли при обучении новые связи между нейронами, не отображенные в исходной структуре?
5. Как на основе анализа транзитивных связей корректируется обучаемая структура нейронной сети?
6. В чем заключается (на иллюстративном уровне) идея трассировки логической нейронной сети?