О деревьях
Представления деревьев
Каждому дереву можно поставить в соответствие некоторый код. С помощью этого кода можно восстановить дерево с точностью до изоморфизма. Существуют различные способы кодировки деревьев, которые позволяют решать конкретные задачи (подсчет деревьев, установление изоморфизма, генерирование всех неизоморфных деревьев и т.д.). Представлением дерева называется способ записи информации о нем, однозначно и полностью восстанавливающий структуру дерева и позволяющий вычислить его характеристики. Выбор представления зависит от решаемой задачи и способа ее решения. Рассмотрим наиболее распространенные способы задания деревьев.
Представление с помощью матрицы смежности
Это представление является общим для всех видов графов; оно задает граф
с точностью до изоморфизма, но вместе с тем данное представление
неэкономично, так как ненулевыми являются для  -вершинного дерева
только
-вершинного дерева
только 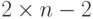 из
из 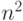 элементов матрицы.
элементов матрицы.
Задание графа матрицей смежности, размера  , где
, где  — число вершин графа.
— число вершин графа.  , если
вершины
, если
вершины  и
и  смежные, в противном случае
смежные, в противном случае  .
.  —
симметрическая матрица
для неориентированного графа и несимметрическая для ориентированного.
—
симметрическая матрица
для неориентированного графа и несимметрическая для ориентированного.
Для неориентированного графа матрица смежности симметрична относительно главной диагонали, поэтому можно задавать только верхнюю треугольную половину матрицы, но это не улучшает ситуацию. Другой недостаток этого представления заключается в том, что трудоемкость алгоритмов, работающих с таким представлением, не может быть ниже.
Пример.

Представление с помощью списков смежности
В этом представлении каждой вершине дерева сопоставляется список смежных
вершин вида 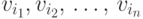 .
.
Для дерева из предыдущего примера списки смежности имеют вид

При машинной организации списки смежности могут быть связаны между собой разными способами, например, копируя структуру дерева.

