Некоторые определения теории графов
Определения и примеры
Матрицей смежности графа  с множеством
вершин
с множеством
вершин 
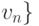 (соответствующей данной
нумерации вершин) называется матрица
(соответствующей данной
нумерации вершин) называется матрица 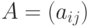 размера
размера  , в которой элемент
, в которой элемент  равен числу ребер в
равен числу ребер в  ,
соединяющих
,
соединяющих 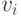 и
и 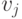 .
Можно получить несколько различных матриц смежности данного графа, меняя
обозначения его вершин. Это приведет к изменению порядка строк и столбцов
матрицы
.
Можно получить несколько различных матриц смежности данного графа, меняя
обозначения его вершин. Это приведет к изменению порядка строк и столбцов
матрицы  . Но в результате всегда получится симметричная матрица
из неотрицательных целых чисел, обладающая тем свойством, что сумма чисел
в любой строке или столбце равна степени соответствующей вершины. Каждая
петля учитывается в степени вершины один раз. Обратно, по любой заданной
симметричной матрице из неотрицательных целых чисел легко построить граф,
единственный с точностью до изоморфизма, для которого данная матрица
является матрицей смежности. Отсюда следует, что теорию графов можно
свести к изучению матриц особого типа.
. Но в результате всегда получится симметричная матрица
из неотрицательных целых чисел, обладающая тем свойством, что сумма чисел
в любой строке или столбце равна степени соответствующей вершины. Каждая
петля учитывается в степени вершины один раз. Обратно, по любой заданной
симметричной матрице из неотрицательных целых чисел легко построить граф,
единственный с точностью до изоморфизма, для которого данная матрица
является матрицей смежности. Отсюда следует, что теорию графов можно
свести к изучению матриц особого типа.
Матрицей инциденций простого графа с множеством вершин 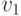 ,...
,... 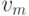 называется матрица
называется матрица 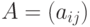 размера
размера  , у которой
, у которой 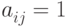 , если вершина
, если вершина 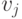 инцидентна ребру
инцидентна ребру 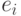 ,
и
,
и 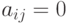 , в противном случае.
, в противном случае.
Граф, у которого множество ребер пусто, называется вполне
несвязным или пустым графом. Будем обозначать вполне
несвязный граф с  вершинами через
вершинами через 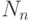 . Простой
граф, в котором любые две вершины смежны, называется полным графом.
Полный граф с
. Простой
граф, в котором любые две вершины смежны, называется полным графом.
Полный граф с  вершинами обычно обозначается
через
вершинами обычно обозначается
через 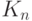 . Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна
. Граф, у которого все вершины имеют одну и ту же степень, называется регулярным графом. Если степень каждой вершины равна  ,
то граф называется регулярным степени
,
то граф называется регулярным степени  .
Регулярные графы степени 3 называются также кубическими,
или трехвалентными графами. Каждый вполне
несвязный граф является регулярным степени
.
Регулярные графы степени 3 называются также кубическими,
или трехвалентными графами. Каждый вполне
несвязный граф является регулярным степени  ,
а каждый полный граф
,
а каждый полный граф 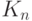 — регулярным
степени
— регулярным
степени  . Среди
регулярных графов особенно интересны платоновы графы —
графы, образованные вершинами и ребрами пяти правильных многогранников —
платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.
. Среди
регулярных графов особенно интересны платоновы графы —
графы, образованные вершинами и ребрами пяти правильных многогранников —
платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.
Объединение и соединение двух графов. Существует несколько
способов соединения двух графов для образования нового, большего графа.
Рассмотрим два из них. Пусть даны
два графа 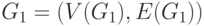 ,
,  ,
причем множества
,
причем множества 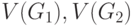 не пересекаются.
Тогда объединением
не пересекаются.
Тогда объединением  графов
графов 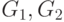 называется граф с множеством
вершин
называется граф с множеством
вершин  и семейством
ребер
и семейством
ребер  . Можно также
образовать соединение
графов
. Можно также
образовать соединение
графов 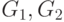 , обозначаемое
, обозначаемое  , взяв их
объединение и соединив ребрами каждую вершину
графа
, взяв их
объединение и соединив ребрами каждую вершину
графа  с каждой вершиной
графа
с каждой вершиной
графа  .
.
Пример матрицы смежности. Пусть дан граф
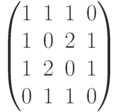
Обхватом графа называется длина его кратчайшего цикла. Множество  ребер графа называется независимым, если оно не содержит циклов,
то есть никакая совокупность ребер из
ребер графа называется независимым, если оно не содержит циклов,
то есть никакая совокупность ребер из  не образует цикла. Диаметром
не образует цикла. Диаметром  связного графа
связного графа  называется максимальное возможное
расстояние между любыми двумя его вершинами. Центром графа
называется максимальное возможное
расстояние между любыми двумя его вершинами. Центром графа  называется такая вершина
называется такая вершина  , что максимальное расстояние
между
, что максимальное расстояние
между  и любой другой вершиной является наименьшим из всех возможных. Это
расстояние называется радиусом
и любой другой вершиной является наименьшим из всех возможных. Это
расстояние называется радиусом  . Таким образом,
. Таким образом,
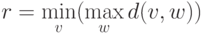 ,
,


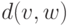 —
—  .
.