|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Экономико-математические модели и принятие решений
Модель экономического роста. В этой модели, в отличие от модели экономического цикла, считается, что предложение денег пропорционально  , и предложение труда пропорционально
, и предложение труда пропорционально 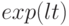 , т.е явно учитываются процессы инфляции и изменение численности необходимой рабочей силы, причем и в том, и в другом случае предполагается экспоненциальный рост.
, т.е явно учитываются процессы инфляции и изменение численности необходимой рабочей силы, причем и в том, и в другом случае предполагается экспоненциальный рост.
Без учета бюджетной политики модель выглядит так:
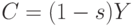 |
( 21) |
 |
( 22) |
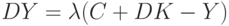 |
( 23) |
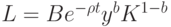 |
( 24) |
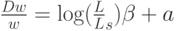 |
( 25) |
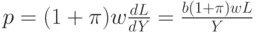 |
( 26) |
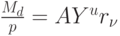 |
( 27) |
 |
( 28) |
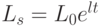 |
( 29) |
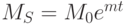 |
( 30) |
где  - численность используемой рабочей силы;
- численность используемой рабочей силы;
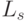 - предложение труда;
- предложение труда;
 - уровень цен;
- уровень цен;
 - ставка заработной платы;
- ставка заработной платы;
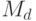 - спрос на деньги;
- спрос на деньги;
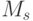 - предложение денег;
- предложение денег;
 - темп роста предложения денег;
- темп роста предложения денег;
 - склонность к сбережениям.
- склонность к сбережениям.
Остальные переменные определены выше при рассмотрении модели экономического цикла.
Уравнение (21) означает, что "доход = сбережение + потребление". Уравнение (22) - формула для нормы прироста основного капитала, аналогичная (7). Уравнение (23) означает, что рост производства равен избытку спроса. Уравнение (24) отражает тот факт, что количество рабочей силы, требуемой для выпуска одного и того же количества продукции, все время убывает благодаря НТР. Таким образом, это уравнение учитывает технический прогресс. Уравнение (25) описывает изменение цен на рынке труда. Уравнение (26) утверждает, что уровень цен равен предельным издержкам (издержки на рабочую силу 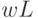 , предельные издержки
, предельные издержки 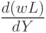 ) плюс некоторая добавка. В уравнении (27)
) плюс некоторая добавка. В уравнении (27) 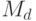 - те активы, которые население желает держать в денежной форме. Реальный спрос на деньги
- те активы, которые население желает держать в денежной форме. Реальный спрос на деньги 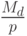 тем выше, чем выше доход
тем выше, чем выше доход  и ниже норма процента r. Уравнение (28) означает, что спрос на деньги равен предложению денег. Это возможно, если считать, что норма процента
все время подстраивается так, чтобы выполнялось это равенство. В уравнении (29) зафиксировано, что предложение труда растет со временем. В уравнении (30) предполагается, что предложение денег растет со временем.
и ниже норма процента r. Уравнение (28) означает, что спрос на деньги равен предложению денег. Это возможно, если считать, что норма процента
все время подстраивается так, чтобы выполнялось это равенство. В уравнении (29) зафиксировано, что предложение труда растет со временем. В уравнении (30) предполагается, что предложение денег растет со временем.
При решении этой системы выяснилось, что, как и раньше, чем больше  , тем стабильнее
, тем стабильнее  и
и  , но в отличие от модели экономического цикла, равновесные
, но в отличие от модели экономического цикла, равновесные  и
и  теперь растут при увеличении
теперь растут при увеличении  - темпа роста и предложения денег.
- темпа роста и предложения денег.
Теперь отразим в модели экономическое регулирование. Существование денежной политики можно выразить заменой уравнения (30) на
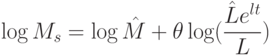 |
( 31) |
где 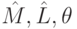 - положительные константы,
- положительные константы,  - оптимальная траектория занятости,
- оптимальная траектория занятости,  - оптимальное предложение денег при оптимальном уровне занятости.
- оптимальное предложение денег при оптимальном уровне занятости.
Чтобы отразить существование государственных расходов и налогов, изменим в системе уравнений (21)-(29), (31) значения некоторых переменных:
C- личное потребление и государственные расходы;
K- сумма государственного и частного основного капитала;
sY- сумма частных и государственных сбережений.
Государственные сбережения - это налоги минус государственные расходы, поэтому, чтобы отразить налоги, сделаем s переменной величиной:
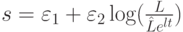 |
( 32) |
где 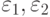 - параметры бюджетной политики. В параметре s учитывается: 1) отношение личного потребления к личному доходу; 2) отношение поступлений от налогов к доходу; 3) отношение текущих государственных расходов к поступлениям от налогов. Все это можно учесть с помощью параметров
- параметры бюджетной политики. В параметре s учитывается: 1) отношение личного потребления к личному доходу; 2) отношение поступлений от налогов к доходу; 3) отношение текущих государственных расходов к поступлениям от налогов. Все это можно учесть с помощью параметров 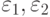 \theta, которые являются управляющими.
\theta, которые являются управляющими.
Модель межотраслевых взаимодействий. Рассмотрим типичную макроэкономическую модель открытого типа (незамкнутую) - модель межотраслевых взаимодействий. Ее формируют две группы математических зависимостей: 1) система уравнений - баланс объема производства каждого вида продукции и его распределение между потребителями (другими производителями и конечными потребителями); 2) система неравенств, которые описывают зависимость между производственными возможностями каждой отрасли и ограничивающими наличными ресурсами (основные фонды и живой труд).
В эту модель нужно ввести извне вектор  - конечный продукт и учесть его деление на потребление, накопление, экспорт, государственные резервы, налоги. Далее, следует задать вектор
- конечный продукт и учесть его деление на потребление, накопление, экспорт, государственные резервы, налоги. Далее, следует задать вектор  - производственные фонды и вектор
- производственные фонды и вектор  - ресурсы живого труда. Это означает, что "вокруг" модели межотраслевых взаимодействий необходимо построить модель доходов и потребления населения - для определения
- ресурсы живого труда. Это означает, что "вокруг" модели межотраслевых взаимодействий необходимо построить модель доходов и потребления населения - для определения  , модель формирования национального дохода - для определения
, модель формирования национального дохода - для определения  , модель "демография - трудовые ресурсы" для определения
, модель "демография - трудовые ресурсы" для определения  и.т.п., то есть создать т.н. макромодельный комплекс.
и.т.п., то есть создать т.н. макромодельный комплекс.
Макроэкономические модели можно условно разделить на два вида. Одни из них описывают, как сказать, типовую страну, без привязки к ее конкретным особенностям. Другие предназначены для использования в конкретных условиях, описывают вполне определенную экономическую реальность. Рассмотрим модели экономики отдельных стран и мирового хозяйства в целом.
Модель влияния государственной финансовой политики на экономику США. В эту модель входят всего 6 переменных, она подходит для аналитического анализа и иллюстрации влияния правительственного фонда заработной платы, правительственного заказа, налога на деловую активность, на личное потребление, заработную плату частного сектора, прибыли, инвестиции, основной капитал и национальных доход.
В рассматриваемой модели переменные управления таковы:
 - правительственный фонд заработной платы на
- правительственный фонд заработной платы на  -м отрезке времени;
-м отрезке времени;
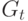 - правительственные заказы на
- правительственные заказы на  -м отрезке времени;
-м отрезке времени;
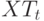 - налог на деловую активность.
- налог на деловую активность.
Используются эндогенные (заданные извне) переменные:
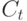 - потребление на
- потребление на  -м отрезке времени,
-м отрезке времени,
 - фонд заработной платы в частном секторе на
- фонд заработной платы в частном секторе на  -м отрезке времени,
-м отрезке времени,
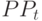 - прибыли на
- прибыли на  -м отрезке времени,
-м отрезке времени,
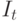 - инвестиции на
- инвестиции на  -м отрезке времени,
-м отрезке времени,
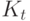 - основной капитал в конце
- основной капитал в конце  -го отрезка времени,
-го отрезка времени,
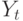 - национальный доход на
- национальный доход на  -м отрезке времени.
-м отрезке времени.
В модель входят уравнения функционирования и тождества. Уравнения функционирования касаются потребления:
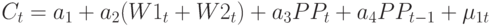
инвестиций:
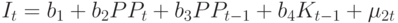
и спроса на рабочую силу:
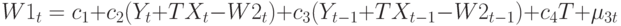
где 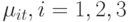 - случайные возмущения.
- случайные возмущения.
Тождества имеют смысл балансовых соотношений (законов сохранения):
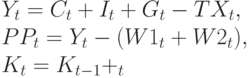
Таким образом, в уравнении потребления зафиксировано, что потребление зависит от заработной платы в частном и государственном секторах, от прибыли в настоящий и предшествующий период времени. В уравнении инвестиций принято, что инвестиции зависят от прибылей в настоящий и предшествующий периоды времени и от основного капитала в предшествующий период времени. Спрос на рабочую силу фактически зависит от прибыльности в настоящий и предшествующий периоды времени.
Коэффициенты в уравнениях и тождествах определяются путем анализа конкретных экономико-статистических данных эконометрическими методами.
Модель экономики США. Существует множество моделей экономики США. Рассмотрим сначала т.н. Уортонскую модель (фактически макромодельный комплекс). Эта модель содержит 734 соотношения, из них 292 уравнения поведения и 442 тождества. Модель состоит из 8 блоков:
- конечный спрос;
- межотраслевые потоки;
- потребность в трудовых ресурсах;
- заработная плата;
- цены производства;
- цены конечного потребления;
- прочие доходы;
- финансы.
Используемые в модели сценарии состоят в том или ином изменении
- федеральных закупок товаров;
- закупок товаров и услуг органами штатов и местного управления;
- трансфертных платежей;
- экспорта;
- налога на инвестиции.
Управляющими параметрами были следующие:
- статьи расходов государственного бюджета;
- ставки налогов;
- цены и заработная плата;
- курс доллара;
- импортные пошлины.
Цель модели - оценка эффективности деятельности федерального правительства. Упрощенная схема этой модели была приведена выше.
Рассмотрим более простую, нежели Уортонская, модель, содержащую гораздо меньше уравнений, однако хорошо иллюстрирующую принципы построения моделей рассматриваемого типа.
Сначала выделяются блоки, из которых будет состоять модель, затем перечисляются переменные, которые входят в модель (их 35). Формируется таблица объясняемых переменных и объясняющих факторов. На основании этой таблицы строится система уравнений. Например, по таблице находим, что основной капитал  зависит от:
зависит от:
-
основного капитала в предшествующий период времени
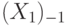 ;
; - инвестиций производственного назначения в предшествующий момент времени
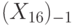 ;
; - краткосрочного процента в предшествующий момент времени
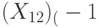 ;
; - возмещения выбытия фондов
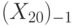 ;
; - занятости в частном секторе
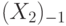 .
.
Теперь строим линейное регрессионное уравнение с авторегрессионным членом:
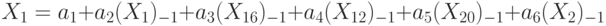
Сложный вопрос состоит в выборе тех переменных, от которых зависит  . Он решается с помощью того или иного алгоритма нахождения "информативного подмножества переменных" в регрессионном анализе. Используются парные и множественные коэффициенты линейной или непараметрической корреляции.
. Он решается с помощью того или иного алгоритма нахождения "информативного подмножества переменных" в регрессионном анализе. Используются парные и множественные коэффициенты линейной или непараметрической корреляции.

 -
-