|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Экономико-математические модели и принятие решений
Модель планирования размеров поставок на базу (склад). В двухуровневой модели накопленный спрос в любой момент времени является случайной величиной. Это не всегда соответствует экономической реальности. Достаточно часто в соответствии с заключенными договорами размеры поставок на базу и объемы запрашиваемой потребителями продукции определены до начала года (с разбивкой по кварталам или по месяцам) и затем не меняются. Однако поставщик имеет право отгружать продукцию, а потребители - забирать ее в течение всего квартала (или месяца).
Опишем соответствующую однопродуктовую модель. Пусть интервал планирования разбит на m периодов, не обязательно одинаковых по продолжительности. В течение каждого периода приходит на базу одна поставка. В 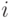 -й период ее величина равна
-й период ее величина равна  , а момент поступления - случайная величина
, а момент поступления - случайная величина  с функцией распределения
с функцией распределения  , где
, где  - отношение времени, прошедшего с начала i-го периода, к продолжительности его,
- отношение времени, прошедшего с начала i-го периода, к продолжительности его,  .
.
В 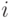 -й период имеется
-й период имеется  потребителей, получающих с базы строго определенное количество продукта,
потребителей, получающих с базы строго определенное количество продукта, 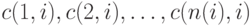 соответственно. Моменты поступления требований от потребителей - случайные величины
соответственно. Моменты поступления требований от потребителей - случайные величины  , с функциями распределения
, с функциями распределения  , где
, где  - отношение времени, прошедшего после начала соответствующего периода, к продолжительности этого периода. Если в момент прихода требования на базе имеется достаточное количество продукта, то он отпускается мгновенно. Если продукта нет, то потребителю придется ждать очередной поставки. Если продукта недостаточно, то весь оставшийся товар отпускается сейчас же, а оставшуюся часть приходится ждать.
- отношение времени, прошедшего после начала соответствующего периода, к продолжительности этого периода. Если в момент прихода требования на базе имеется достаточное количество продукта, то он отпускается мгновенно. Если продукта нет, то потребителю придется ждать очередной поставки. Если продукта недостаточно, то весь оставшийся товар отпускается сейчас же, а оставшуюся часть приходится ждать.
В течение 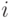 -го периода,
-го периода,  , все моменты поступления товара и требований
, все моменты поступления товара и требований  , предполагаются независимыми в совокупности. Потери, как обычно, складываются из издержек по хранению и от дефицита (расходы на доставку партий заданы заранее, т.е. постоянны, а потому их можно не включать в минимизируемый функционал). Издержки по хранению предполагаются пропорциональными времени хранения и величине запаса с коэффициентами пропорциональности
, предполагаются независимыми в совокупности. Потери, как обычно, складываются из издержек по хранению и от дефицита (расходы на доставку партий заданы заранее, т.е. постоянны, а потому их можно не включать в минимизируемый функционал). Издержки по хранению предполагаются пропорциональными времени хранения и величине запаса с коэффициентами пропорциональности  . Издержки от дефицита складываются из потерь у каждого из потребителей; они пропорциональны величине и длительности дефицита с коэффициентами пропорциональности
. Издержки от дефицита складываются из потерь у каждого из потребителей; они пропорциональны величине и длительности дефицита с коэффициентами пропорциональности 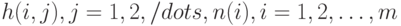 .
.
Пусть 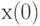 - начальный запас,
- начальный запас,  - количество продукта на базе в конце i-го периода,
- количество продукта на базе в конце i-го периода,  . Пусть
. Пусть 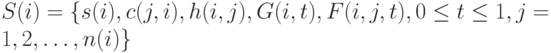 - исходные данные модели в i-й период. Как легко видеть, математическое ожидание издержек за i-й период зависит только от х(i-1), х(i) и S(i). Для краткости обозначим его через
- исходные данные модели в i-й период. Как легко видеть, математическое ожидание издержек за i-й период зависит только от х(i-1), х(i) и S(i). Для краткости обозначим его через  . Тогда математическое ожидание издержек за m периодов равно
. Тогда математическое ожидание издержек за m периодов равно

Необходимо минимизировать  по совокупности переменных. Таким образом, необходимо найти оптимальные значения уровней запаса на складе в начале и в конце периодов. Это эквивалентно определению оптимальных размеров поставок по периодам и начального запаса. Ограничения рассматриваемой оптимизационной задачи выписаны в [13.15] [13.19].
по совокупности переменных. Таким образом, необходимо найти оптимальные значения уровней запаса на складе в начале и в конце периодов. Это эквивалентно определению оптимальных размеров поставок по периодам и начального запаса. Ограничения рассматриваемой оптимизационной задачи выписаны в [13.15] [13.19].
Вначале была сделана попытка рассматривать задачу минимизации 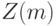 как задачу динамического программирования и решать ее типовыми методами. Однако вычислительных мощностей оказалось недостаточно для выполнения расчетов. Тогда нам удалось показать, что функция
как задачу динамического программирования и решать ее типовыми методами. Однако вычислительных мощностей оказалось недостаточно для выполнения расчетов. Тогда нам удалось показать, что функция  -го переменного
-го переменного 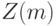 в действительности является суммой
в действительности является суммой  функции одного переменного.
функции одного переменного.
Действительно,

где  - математическое ожидание затрат, произведенных до прихода очередной поставки,
- математическое ожидание затрат, произведенных до прихода очередной поставки,  - математическое ожидание затрат после поступления поставки.
- математическое ожидание затрат после поступления поставки.
Ясно, что  определяется запасом на начало периода и спросом до прихода поставки, но не зависит от запаса на конец периода, т.е. от
определяется запасом на начало периода и спросом до прихода поставки, но не зависит от запаса на конец периода, т.е. от  . Таким образом, можно записать, что
. Таким образом, можно записать, что
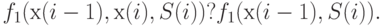
Пусть  - объем поставки на склад в i-й период. Сразу же после прихода поставки запас
- объем поставки на склад в i-й период. Сразу же после прихода поставки запас  на складе равен
на складе равен
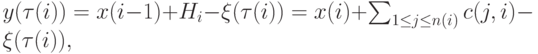
где 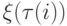 - накопленный с начала периода спрос. Поскольку
- накопленный с начала периода спрос. Поскольку 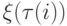 не зависит от
не зависит от  , то и
, то и  не зависит от
не зависит от  . Итак,
. Итак,

Следовательно, минимизируемая функция имеет вид

При этом ограничения наложены на каждую переменную  по отдельности [20, 27]. Ясно, что задача минимизации
по отдельности [20, 27]. Ясно, что задача минимизации 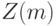 распадается на
распадается на 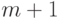 задачу минимизации функций одной переменной:
задачу минимизации функций одной переменной:

 |
( 45) |

(ограничения не указаны). Следовательно, 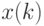 зависит только от исходных данных смежных периодов
зависит только от исходных данных смежных периодов  и
и 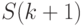 и остается неизменным при любом изменении
и остается неизменным при любом изменении  . Из указанного разложения задачи многомерной оптимизации на ряд задач одномерной оптимизации вытекает также, что при планировании на
. Из указанного разложения задачи многомерной оптимизации на ряд задач одномерной оптимизации вытекает также, что при планировании на  и
и  периодов совпадают оптимальные значения начального запаса и поставок за первые min
периодов совпадают оптимальные значения начального запаса и поставок за первые min  периодов. В частном случае стационарного режима
периодов. В частном случае стационарного режима  , оптимальный план имеет вид
, оптимальный план имеет вид  , где
, где 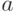 - решение первой из указанных в (45) задач,
- решение первой из указанных в (45) задач, 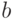 - решение второй задачи и
- решение второй задачи и  - третьей.
- третьей.
Переход к задачам (45) не только позволяет решить исходную задачу минимизации (напомним, что для минимизации задачи в исходной форме не хватало вычислительных мощностей), но также получить весьма важный для экономической интерпретации вывод о независимости оптимальных значений поставок и начального запаса от горизонта планирования m.
Важное замечание 4. Рассмотренная модель дает хороший пример пользы математического анализа оптимизационной задачи принятия решений. Такой анализ позволяет решать задачу не стандартными методами, требующими больших вычислительных ресурсов, а с помощью специально разработанных алгоритмов, учитывающих специфику задачи и позволяющих на много порядков сократить вычисления. Плата за экономию вычислительных ресурсов - необходимость квалифицированного труда специалистов по экономико-математическим методам и прикладной математике.
В настоящее время логистика - одна из экономических дисциплин, весьма развитая как в теоретическом, так и в практическом отношении. В ней рассматривается масса конкретных моделей управления запасами. Из перспективных направлений назовем использование случайных множеств в моделях логистики. Моделирование с целью нахождение оптимальных решений было выше продемонстрировано на примерах системы моделей, исходящих из классической модели Вильсона, двухуровневой модели, модели оптимизации объемов поставок на базу (склад).
Контрольные вопросы и задачи
- На основе паутинообразной модели ответьте на вопрос, всегда ли цена и объем выпуска приближаются к равновесным.
- Чем модель экономического роста отличается от модели экономического цикла?
- Каковы переменные управления в модели влияния государственной финансовой политики на экономику США?
- Какова роль блоков в создании макромодельных комплексов?
- Чем экономико-математическая модель малого предприятия типа "поток проектов" отличается от модели типа "занятие ниши"?
- На складе хранится некоторая продукция, пользующаяся равномерным спросом. За 1 день со склада извлекается 0,5 т продукции, плата за хранение 1 т продукции в день - 2 тыс. руб., плата за доставку одной партии - 50 тыс. руб. Планирование производится на 21 день. На сколько процентов затраты в плане Вильсона (объем партии определяется по формуле квадратного корня) превышают затраты в оптимальном плане?
- Оцените увеличение затрат в плане Вильсона (объем партии определяется по формуле квадратного корня) по сравнению с оптимальным планом за целое число периодов, если размер партии отличается от оптимального не более чем на 5%.
- Каким образом концепция асимптотически оптимального плана позволяет решить проблему горизонта планирования при принятии логистических решений?
- В чем состоит основной вклад математики при разработке модели планирования оптимальных размеров поставок и начального запаса?
Темы докладов и рефератов
- Комплексные системы управления качеством продукции и международные стандарты ИСО по менеджменту качества.
- Экономическая эффективность усеченных планов статистического приемочного контроля.
- Взаимосвязь технического уровня, качества и конкурентоспособности продукции.
- Методы проведения статистического приемочного контроля порошкообразных материалов.
- Различные варианты взаимодействия поставщика и потребителя в связи с системой принятием решений о качестве продукции.
- Программное обеспечение статистических методов управления качеством продукции.
