НОУ ИНТУИТ | Менеджмент высоких технологий. Лекция 6: Повышение эффективности корпоративных производственно-сбытовых структур (ПСС) в области сбыта и товаропродвижения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.09.2009 | Доступ: свободный | Студентов: 1568 / 252 | Оценка: 4.10 / 4.10 | Длительность: 42:50:00

Тема: Менеджмент

Специальности: Менеджер, Руководитель

|

Вам нравится? Нравится 28 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

В данной лекции при прогнозировании спроса предлагается использовать достаточно эффективные экспертные методы [13, гл.12]. Для получения данных оценок наиболее приемлемыми являются коллективные экспертные оценки, в частности, метод Дельфи.

Согласно этому методу, определяя возможные границы прогнозируемой величины, каждый из экспертов дает два значения - минимальное и максимальное, между которыми находится прогнозируемая величина.

В качестве плотности распределения прогнозируемой величины условно принимается равномерная плотность:

$f(Y_i) = \cfrac{1}{Y_{i,max} - Y_{i,min}}, \text{ где } Y_{i,min} \le Y_i \le Y_{i,max}$

Среднее значение прогноза -го эксперта:

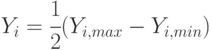$Y_i = \cfrac{1}{2}(Y_{i,max} - Y_{i,min})$

( 6.4)

Точечный прогноз всей группы (при одинаковых весах экспертов):

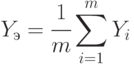$Y_э = \cfrac{1}{m}\sum\limits_{i=1}^{m}Y_i$

( 6.5)

где - количество экспертов.

Выборочная дисперсия точечных прогнозов -х экспертов относительно $Y_{Э}$ :

$D(Y) = \cfrac{1}{m-1}\sum\limits_{i=1}^{m}{(Y'_i - Y_i)^2}$

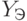( 6.5)

Коэффициент вариации, характеризующий единодушие экспертов по точечным прогнозам:

= \cfrac{\sigma}{Y},

где 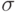$\sigma$ - выборочное среднеквадратичное отклонение прогноза.

$\sigma = \sqrt{D(Y)}$

( Y))

Для исследования влияния цены -го товара на уровень спроса на него прогноз следует проводить по нескольким направлениям:

прогнозирование распределения потребности в каждом виде изделий по периодам прогнозирования:
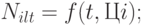
$N_{ilt} = f(t,Цi);$
определение зависимости рыночной цены на каждый вид изделий по периодам прогнозирования:
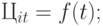
$Ц_{it} = f(t);$
прогнозирование объемов продаж продукции в зависимости от ее техникоэкономического уровня и цены.
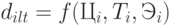
$d_{ilt} = f(Ц_{i},T_{i},Э_{i})$

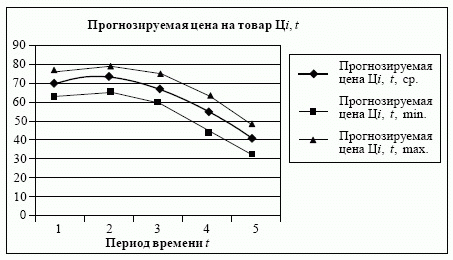
Таким образом, группа экспертов для каждого момента времени дает точечные групповые прогнозы потребности и цены реализуемых изделий. Распределяя полученные оценки во времени, получают гистограммы (рис. 6.16-6.17) распределения потребности (причем оценивается максимально возможный уровень спроса на прогнозируемый период для каждого вида изделий 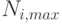$N_{i,max}$ и минимальный уровень спроса, соответствующий негативному стечению факторов, формирующих спрос $N_{i,min}$ ).

Рис. 6.16. График прогнозируемой цены на товар

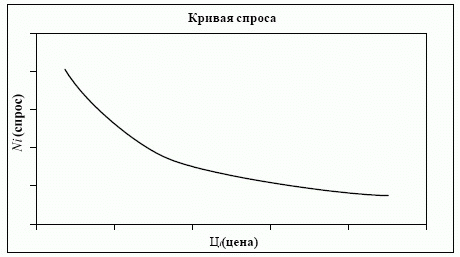
На основе построенных кривых можно определить коэффициент эластичности спроса, отражающий степень чувствительности потребителей к изменению цены:

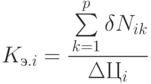
$K_{э.i} = \cfrac{\sum\limits_{k=1}^{p}{\delta N_{ik}}}{\Delta Ц_i}$

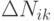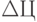где $\Delta N_{ik}$ - изменение объема запрашиваемого товара потребителем на исследуемом рынке, произошедшее вследствие изменения цены $\Delta Ц$ .

На основании гистограмм распределения потребности в каждом виде изделий и их цен по периодам прогнозирования, а также кривых спроса (рис. 6.18 - метод оценивания дан в [13, гл.2]) может проводиться краткосрочное, среднесрочное и долгосрочное прогнозирование. Однако гистограммы распределения потребности в товаре не учитывают влияния чрезвычайных факторов, вызывающих колебания спроса, наиболее значительными из которых можно считать: региональный или глобальный экономический кризис, появление новых товаровзаменителей у конкурентов, изменение спроса вследствие свертывания производств (на рынке производственных ресурсов) и др. Полученные данные необходимо в конечном итоге корректировать с помощью мнений экспертов различными методами. Но тем не менее приблизительные значения потребности в изделиях, которые будут использоваться в дальнейших расчетах по каждому элементу сбытовой цепи или группы элементов, а также в исследуемом сегменте рынка, могут быть получены, исходя из вышеизложенной процедуры.

Рис. 6.17. График прогнозируемого спроса на товар

Рис. 6.18. Кривая спроса

Выбор критериев и моделирование систем сбыта. Под моделированием системы сбыта понимается как создание структуры системы сбыта, так и разработка вариантов товародвижения в этой структуре.

Система сбыта предприятия характеризуется многими характеристиками. Для задачи выбора оптимального варианта структуры сбыта и систем товародвижения следует исходить из определенных критериев, часть из которых следует предварительно рассчитать, а часть оценить субъективно по определенным методикам.

При моделировании сбытовых структур техникоэкономическому анализу подвергаются следующие показатели:

число возможных посредников или уровней собственной системы, исходя из отпускной цены, из сложившейся рыночной цены и вероятных торговых наценок, которые сделает каждый участник канала;
типы звеньев сбытовой цепи по юридическому и экономическому признакам и по тому объему товара, который они способны закупать;
схема управления сбытовой системой и координация работы с посредниками;
принципы определения цены и взаиморасчетов производителя и посредников;
вариативность логистики распределения: склады, транспорт.

Таким образом, для характеристики структуры сбыта и системы товародвижения имеет смысл анализировать следующие критерии:

прогнозируемая прибыль Пmax или чистая текущая стоимость проекта 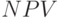(расчет определен ниже);
затраты на создание структуры $S_{созд}$ . (в случае рассмотрения по критерию 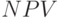- затраты на создание включаются в чистую текущую стоимость проекта в виде инвестиций или амортизируются);
гибкость (субъективная оценка);
объемы реализации (или процент удовлетворения спроса);
доля рынка или географический охват территории (условный процент);

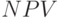Основным критерием системы распределения организации является величина финансовой отдачи ( Пmax и NPV ), которую может получить ПСС при реализации своей продукции с помощью создаваемой сбытовой структуры.

Именно этот критерий является основополагающим при предварительном отборе тех или иных вариантов структур систем сбыта. Также величина прогнозируемой прибыли в конечном итоге станет основным показателем и при выборе окончательного варианта.

Процесс моделирования сбытовой структуры ПСС, изложенный в дальнейшем, будет иметь выходной результат - прогнозируемую прибыль, а входные данные - структура системы сбыта. Имеется производственно-сбытовая система, производящая товары определенной номенклатуры. На исследуемом рынке (рынке товаров народного потребления или производственного назначения) существует конкуренция определенного вида. Соотношение спроса и предложения на нем составляют определенную конъюнктуру данного рынка. Количество производимых или ввозимых изделий по всей номенклатуре прогнозируется или изначально задано. Товар находится на крупнооптовых складах ПСС по видам изделий. Необходимо реализовать товар с максимальной выгодой, т. е. максимизировать в общем виде целевую функцию (из (6.1)).

Можно создавать многономенклатурные оптовые склады, а также дальнейшие звенья сбытовой цепи вплоть до доставки товаров конечным потребителям. Создание каждого звена цепи приводит к увеличению суммарных затрат ПСС, а также затрат на создание самой сбытовой структуры $S _{созд}$ . Поэтому цена реализации на более нижнем уровне возрастает на определенную величину, которая зависит от затрат по содержанию склада (магазина, отдела) и от стоимости доставки товара в указанный пункт. С другой стороны, можно не создавать дальнейшие уровни собственной сбытовой цепи и реализовывать товар исключительно крупными партиями по оптовым ценам, что в общем случае чревато потерей определенной части потребителей. Каждое дополнительное звено сбытовой структуры в общем случае открывает новые сбытовые возможности, особенно в случае регионального расширения, по схеме:

Новое звено

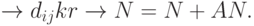
$\to d_{ij}kr \to N = N+AN.$

Но с другой стороны

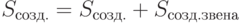
$S_{созд.} = S_{созд.} + S_{созд.звена}$

Кроме того, у предприятия могут быть в отличие от получения максимальной прибыли нестандартные стратегические задачи: завоевание новых рынков, занимаемая доля рынка. Это показывает такой критерий, как географический охват территории, который может быть как расчетным, субъективным, так и сочетающим в себе расчет и суждения.

Процесс моделирования систем - варьирование переменных структуры сбытовой системы и величин материальных потоков (товародвижения) в ней для расчета анализируемого показателя (из (6.1)) на основе входных данных (рис. 6.19).

Рис. 6.19. Схема моделирования товародвижения и оптимизации

Сущность модели заключается в необходимости разработки каналов и расчета потоков продвижения товаров по этим каналам к потребителям, чтобы максимизировать целевую функцию прибыли. В зависимости от поставленной задачи, типа рынка, и требований к результату следует пользоваться различными методами.

Метод 1.

В первом случае моделирования допускается, что весь товар будет реализован из любого элемента ПСС, а также не учитывается временная характеристика (модель рассматривается статически).

Ранее введены следующие величины:

- количество изделий по номенклатуре (число крупноооптовых складов верхнего уровня);

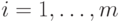$i = 1,\dots ,m$ - индекс изделия (номер оптового склада);

- число уровней в моделируемой системе сбыта (вкл. нулевой);

$r = 0,\dots ,R$ - индекс уровня;

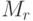$M_{r}$ - число складов (магазинов) на уровне ;

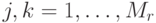$j,k = 1,\dots , M_{r}$ - индексы магазинов (складов, отд. потребителей).

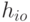$h_{io}$ - запас -го изделия на 0-м уровне (на -м оптовом складе).

$S_{prodi}$ - затраты на производство единицы -го изделия (допускается, что переменные затраты на производство (покупку) товаров прямо пропорциональны их количеству).

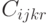$C_{ijkr}$ - затраты на транспортировку единицы продукции из склада (магазина) уровня r-1 в пункт уровня .

Для упрощения модели допускается, что величина транспортных затрат прямо пропорциональна количеству перемещаемых изделий, а себестоимость единицы перевозки не зависит от размера партии. В дальнейшем данные условия можно изменить в зависимости от специфики товара.

$S_{transp}$ - суммарные затраты на транспортировку.

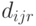$d_{ijr}$ - запрос (потребность, заказ) -го изделия в -м пункте уровня . Эти величины либо составляют на основе сделанных заказов на товар, либо исходя из прогнозируемых величин спроса.

Ц $_{io}$ - цена реализации (устанавливаемая) на верхнем (нулевом) оптовом уровне (оптовая цена);

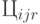$Ц_{ijr}$ - цена реализации изделия в -м пункте -го уровня;

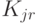$K_{jr}$ - коэффициент изменения цены в -м магазине -го уровня;

Данная величина отражает изменение цены при продвижении вниз по цепочке сбыта:

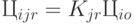
$Ц_{ijr} = K_{jr}Ц_{io}$

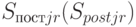$S_{пост jr} (S_{post jr})$ - постоянные расходы по функционированию звена на уровне . Создание каждого нового звена цепи приводит к увеличению суммарных затрат ПСС на вышеуказанную величину.

Требуется определить $X_{ijkr}$ , где $X_{ijkr}$ - количество товара вида , перемещаемое для дальнейшей перепродажи самой системой из склада (магазина) уровня r-1 в пункт уровня .

После введения обозначений можно определить следующие величины:

Выручка от продажи изделия в -м магазине:

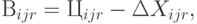$В_{ijr} = Ц_{ijr}-\Delta X_{ijr},$

( 6.6)

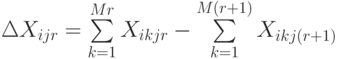
где $\Delta X_{ijr} = \sum\limits_{k=1}^{Mr}{X_{ikjr}} - \sum\limits_{k=1}^{M(r+1)}{X_{ikj(r+1)}}$

т. е. разница в количестве товара -ой номенклатуры, оставшаяся в пункте (т. е. суммарное число ввезенного товара в пункт уровня за вычетом вывезенного из данного звена ПСС).

Таким образом:

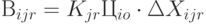$В_{ijr} = K_{jr}Ц_{io}\cdot \Delta X_{ijr}$

( 6.7)

Выручка от продажи всех изделий в -м магазине -го уровня (суммирование по видам изделий:

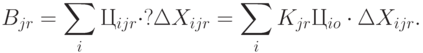$B_{jr} = \sum\limits_i{Ц_{ijr}\cdot? \Delta X_{ijr} = \sum\limits_i {K_{jr}Ц_{io} \cdot \Delta X_{ijr}.$

( 6.8)

Выручка на -м уровне ПСС:

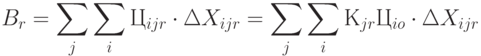$B_r = \sum\limits_{j}{\sum\limits_{i}{Ц_{ijr} \cdot \Delta X_{ijr} }}= \sum\limits_{j}{\sum\limits_{i}{К_{jr}Ц_{io} \cdot \Delta X_{ijr}}}$

( 6.9)

Прибыль на -м уровне (без учета транспортных затрат):

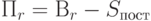$П_{r} = В_{r} - S_{пост}$

( 6.1)

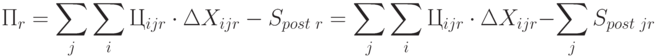
$П_r = \sum\limits_{j}{\sum\limits_{i}{Ц_{ijr} \cdot \Delta X_{ijr} - S_{post\text{ }r} }} = \sum\limits_{j}{\sum\limits_{i}{Ц_{ijr} \cdot \Delta X_{ijr}}} - \sum\limits_{j}{S_{post\text{ }jr}}}$

Прибыль всей ПСС без учета транспортных затрат:

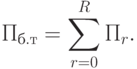
$П_{б.т} = \sum\limits_{r=0}^{R}{П_r .}$

Прибыль всей ПСС с учетом транспортных затрат и затрат на изготовление:

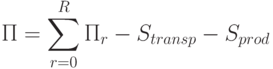$П = \sum\limits_{r=0}^{R}{П_r}- S_{transp}-S_{prod}$

( 6.11)

Подставляя полученные ранее выражения, получаем:

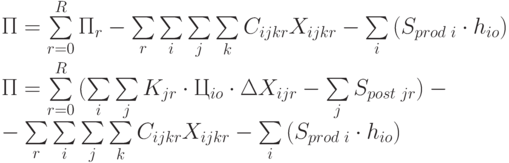$П =\sum\limits_{r=0}^{R}{П_r} - \sum\limits_{r}{\sum\limits_{i}{\sum\limits_{j}{\sum\limits_{k}{C_{ijkr} X_{ijkr}}}}} - \sum\limits_{i}{(S_{prod\text{ }i}\cdot h_{io}})} \\ П =\sum\limits_{r=0}^{R}{(\sum\limits_{i}{\sum\limits_{j}{K_{jr}\cdot Ц_{io} \cdot \Delta X_{ijr}}} - \sum\limits_{j}{S_{post\text{ }jr}})} - \\ - \sum\limits_{r}{\sum\limits_{i}{\sum\limits_{j}{\sum\limits_{k}{C_{ijkr} X_{ijkr}}}}} - \sum\limits_{i}{(S_{prod\text{ }i}\cdot h_{io}})}$

( 6.12)

Данная формула отражает численный результат, полученный в результате моделирования ПСС. Задача создания оптимальной системы сбыта в общем случае сводится к максимизации прибыли.

Целевая функция $П \to max$ . Вводятся ограничения: