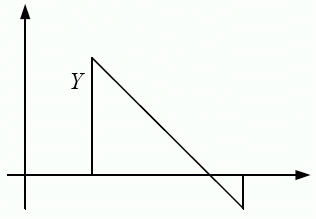|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Организационно-экономическая система управления материальными запасами промышленных корпоративных систем
На первый взгляд, представляется удивительным, что сравнительно большое отклонение значения переменной  от оптимального (на 30%) приводит к столь малому возрастанию значения оптимизируемой функции. Этот факт имеет большое прикладное значение. Из него следует, что область "почти оптимальных" значений параметра весьма обширна, следовательно, из нее можно выбирать для практического использования те или иные значения исходя из иных принципов. Можно, например, минимизировать какую-либо иную целевую функцию, тем самым решая задачу многокритериальной оптимизации. Можно "вписаться" в действующую дискретную систему возможных значений параметров. И т. д.
от оптимального (на 30%) приводит к столь малому возрастанию значения оптимизируемой функции. Этот факт имеет большое прикладное значение. Из него следует, что область "почти оптимальных" значений параметра весьма обширна, следовательно, из нее можно выбирать для практического использования те или иные значения исходя из иных принципов. Можно, например, минимизировать какую-либо иную целевую функцию, тем самым решая задачу многокритериальной оптимизации. Можно "вписаться" в действующую дискретную систему возможных значений параметров. И т. д.
Важное замечание 1.Обширность области "почти оптимальных" значений параметра - общее свойство оптимальных решений, получаемых путем минимизации гладких функций. Действительно, пусть необходимо минимизировать некоторую функцию  , трижды дифференцируемую. Пусть минимум достигается в точке
, трижды дифференцируемую. Пусть минимум достигается в точке 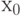 . Справедливо разложение Тейлора-Маклорена
. Справедливо разложение Тейлора-Маклорена
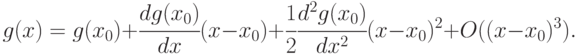
Однако в 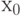 выполнено необходимое условие экстремума (в данном случае - минимума)
выполнено необходимое условие экстремума (в данном случае - минимума)
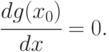
Следовательно, с точностью до бесконечно малых более высокого порядка (по сравнению с 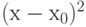 ) справедливо равенство
) справедливо равенство
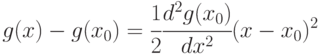 |
( 4.9) |
Это соотношение показывает, что приращение значений минимизируемой функции - бесконечно малая более высокого порядка по сравнению с приращением независимой переменной. Если

то
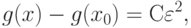
где
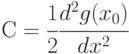
Вернемся к классической модели управления запасами. Для нее надо рассматривать 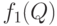 в роли
в роли  . С помощью соотношения (6.9) заключаем, что
. С помощью соотношения (6.9) заключаем, что
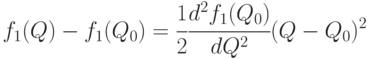
с точностью до бесконечно малых более высокого порядка. Вычислим вторую производную 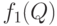 . Поскольку
. Поскольку
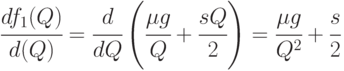
то
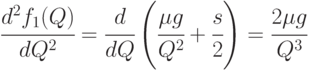
Теперь заметим, что
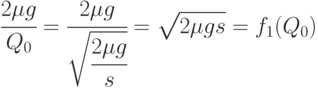
Следовательно,
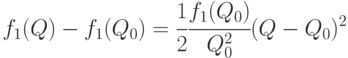
с точностью до бесконечно малых более высокого порядка. Отличие этой формулы от точной формулы (6.8) состоит только в том, что  в знаменателе одной из дробей заменено на
в знаменателе одной из дробей заменено на 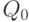 .
.
Устойчивость выводов в математической модели.Вполне ясно, что рассматриваемая классическая модель управления запасами, как и любые иные экономико-математические модели конкретных экономических явлений и процессов, лишь приближение к реальности. Приближение может быть более точным или менее точным, но никогда не может полностью уловить все черты реальности. Поэтому с целью повышения адекватности получаемых на основе экономико-математической модели выводов целесообразно изучить устойчивость этих выводов по отношению к допустимым отклонениям исходных данных и предпосылок модели [13, 11]. Выше изучено изменение средних издержек при малых отклонениях величины поставки.
Предположим теперь, что вместо истинных значений параметров 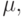
 ,
,  нам известны лишь их приближенные значения
нам известны лишь их приближенные значения 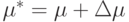 ,
,  ,
, 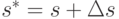 . Мы применяем план Вильсона, но с искаженным объемом партии
. Мы применяем план Вильсона, но с искаженным объемом партии
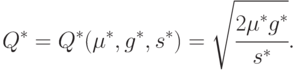
Это приводит к возрастанию средних издержек. Согласно формулам (4.8)-(4.9) возрастание пропорционально 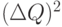 (с точностью до бесконечно малых более высокого порядка). Здесь
(с точностью до бесконечно малых более высокого порядка). Здесь
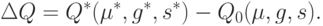
Выделим в 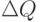 главный линейный член:
главный линейный член:
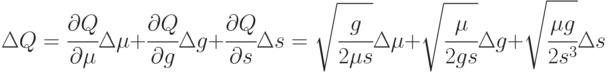 |
( 4.10) |
(с точностью до бесконечно малых более высокого порядка).
Величину 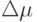 можно определить по фактическим данным о спросе, оценив величину отклонения реального спроса от линейного приближения [11], например, с помощью математического аппарата линейного регрессионного анализа [13]. Для определения значений параметров
можно определить по фактическим данным о спросе, оценив величину отклонения реального спроса от линейного приближения [11], например, с помощью математического аппарата линейного регрессионного анализа [13]. Для определения значений параметров  и
и  необходимо проведение специальных трудоемких исследований. К тому же существуют различные методики расчета этих параметров, результаты расчетов по которым не совпадают. Поэтому естественно оценить разумную точность определения
необходимо проведение специальных трудоемких исследований. К тому же существуют различные методики расчета этих параметров, результаты расчетов по которым не совпадают. Поэтому естественно оценить разумную точность определения  и
и  по известной точности определения
по известной точности определения 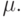 Для этого воспользуемся "принципом уравнивания погрешностей", предложенным в [11].
Для этого воспользуемся "принципом уравнивания погрешностей", предложенным в [11].
Важное замечание 2.Принцип уравнивания погрешностей состоит в том, что погрешности различной природы должны вносить примерно одинаковый вклад в общую погрешность математической модели. Так, определение рационального объема выборки в статистике интервальных данных основано на уравнивании влияния метрологической и статистической погрешностей. Согласно подходу [11], выбор числа градаций в социологических анкетах целесообразно проводить на основе уравнивания погрешностей квантования и неопределенности в ответах респондентов. В классической модели управления запасами целесообразно уравнять влияние неточностей в определении параметров на отклонение целевой функции от оптимума.
Выберем 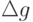 и
и 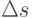 так, чтобы увеличение затрат, вызванное неточностью определения
так, чтобы увеличение затрат, вызванное неточностью определения  и
и  , было таким же, как и вызванное неточностью определения
, было таким же, как и вызванное неточностью определения 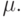 С точностью до бесконечно малых более высокого порядка это означает, что необходимо уравнять между собой три слагаемых в правой части (4.10). После сокращения общего множителя получаем, что согласно принципу уравнивания погрешностей должно быть справедливо соотношение
С точностью до бесконечно малых более высокого порядка это означает, что необходимо уравнять между собой три слагаемых в правой части (4.10). После сокращения общего множителя получаем, что согласно принципу уравнивания погрешностей должно быть справедливо соотношение
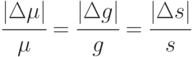 |
( 4.11) |
Таким образом, относительные погрешности определения параметров модели должны совпадать.
В соотношении (4.11) используются истинные значения параметров, которые неизвестны. Поэтому целесообразно вначале вместо параметров использовать их грубые оценки, из (4.11) определить их примерную точность, затем провести исследования, уточняющие значения параметров. Эту процедуру целесообразно повторять до тех пор, пока не произойдет некоторое уравнивание относительных погрешностей определения параметров модели.
Модель с дефицитом.Классическая модель управления запасами может быть обобщена в различных направлениях. Одно из наиболее естественных обобщений - введение в модель возможности дефицита.
В рассматриваемой до сих пор модели предполагалось, что дефицит не допускается, т. е. некоторое количество товара на складе всегда есть. Но, может быть, выгоднее сэкономить на расходах по хранению запаса, допустив небольшой дефицит, - потребность в товаре в некоторые интервалы времени может остаться неудовлетворенной?
Как подсчитать убытки от дефицита, в частности, от потери доверия потребителя? Будем считать, что если нет товара, владеющая складом организация платит штраф - каждый день пропорционально нехватке. По приходе очередной поставки все накопленные требования сразу же удовлетворяются.
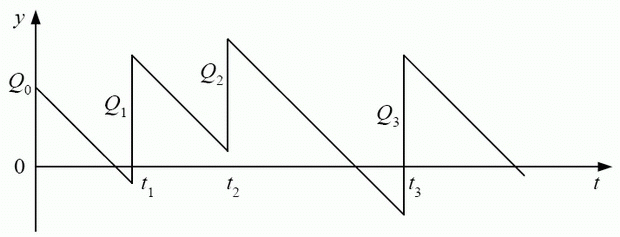
Сохраним все предположения и обозначения рассматриваемой до сих пор модели, кроме отсутствия дефицита. Неудовлетворенный спрос будем рассматривать как отрицательный запас. График изменения величины запаса на складе изображен на рис. 4.3.
Очевидно, рис. 4.1 и рис. 4.3 отличаются только тем, что на последнем рисунке зубцы графика могут опускаться ниже оси абсцисс, что соответствует сдвигу графика рис. 4.1 как единого целого вниз вдоль оси ординат.
Пусть  - плата за нехватку единицы товара в единицу времени (например, в день). Тогда средние издержки за время
- плата за нехватку единицы товара в единицу времени (например, в день). Тогда средние издержки за время  определяются формулой
определяются формулой
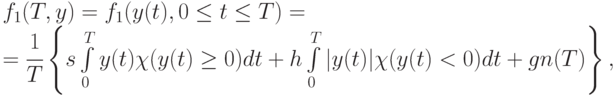
где  - индикатор множества
- индикатор множества  , т. е.
, т. е.  при
при 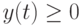 и
и  при
при 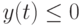 , в то время как
, в то время как  при
при 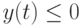 и
и  при
при 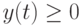 . Таким образом, площадь под частью графика уровня запаса, лежащей выше оси абсцисс, берется с множителем
. Таким образом, площадь под частью графика уровня запаса, лежащей выше оси абсцисс, берется с множителем  , а площадь между осью абсцисс и частью графика
, а площадь между осью абсцисс и частью графика 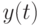 , соответствующей отрицательным значениям запаса, берется с заметно большим по величине множителем
, соответствующей отрицательным значениям запаса, берется с заметно большим по величине множителем  .
.
Для модели с дефицитом оптимальный план находится почти по той же схеме, что и для модели без дефицита. Сначала фиксируем моменты поставок и находим при этом условии оптимальные размеры поставок. Фактически речь идет о выборе уровня запаса  в момент прихода очередной поставки (рис. 4.4).
в момент прихода очередной поставки (рис. 4.4).
Увеличивая или уменьшая  , можно увеличивать или уменьшать площадь треугольника над осью абсцисс (учитываемую с коэффициентом
, можно увеличивать или уменьшать площадь треугольника над осью абсцисс (учитываемую с коэффициентом  ) и соответственно уменьшать или увеличивать площадь треугольника под осью абсцисс (учитываемую с коэффициентом
) и соответственно уменьшать или увеличивать площадь треугольника под осью абсцисс (учитываемую с коэффициентом  ), добиваясь минимизации взвешенной суммы этих площадей. Все элементы прямоугольных треугольников на рис. 4.4 выражаются через
), добиваясь минимизации взвешенной суммы этих площадей. Все элементы прямоугольных треугольников на рис. 4.4 выражаются через  , заданный интервал времени между поставками и параметры модели. Минимизация соответствующего квадратного трехчлена дает оптимальное значение
, заданный интервал времени между поставками и параметры модели. Минимизация соответствующего квадратного трехчлена дает оптимальное значение
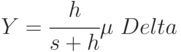
При этом минимальная сумма затрат на хранение и издержки, вызванные дефицитом, равна
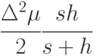
Второй шаг нахождения оптимального плана в модели с дефицитом полностью совпадает с аналогичным рассуждением в исходной модели. Фиксируется число поставок, и с помощью варьирования размеров интервалов между поставками минимизируется целевой функционал. Поскольку сумма квадратов некоторого числа переменных при заданной их сумме достигает минимума, когда все эти переменные равны между собой, то оптимальным планом является план, у которого все зубцы одинаковы, т. е. уровень запаса в момент прихода очередной поставки - всегда один и тот же. При этом все объемы поставок, за исключением объема начальной поставки (в нулевой момент времени), равны между собой:
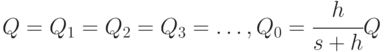 |
( 4.12) |
На третьем этапе среди указанного однопараметрического дискретного множества планов находим оптимальный план. Как и для модели без дефицита, в качестве ориентира используется план с размером поставки, определяемой по формуле квадратного корня,
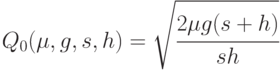
Для горизонтов планирования  , кратных
, кратных 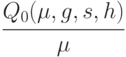 , оптимальным является план типа (4.12) с
, оптимальным является план типа (4.12) с  . Для всех остальных горизонтов планирования, как и в случае модели без дефицита, необходимо найти неотрицательное целое число
. Для всех остальных горизонтов планирования, как и в случае модели без дефицита, необходимо найти неотрицательное целое число  такое, что
такое, что
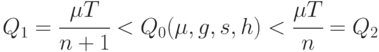
а затем, сравнив издержки для  и
и  , объявить оптимальным то из этих двух значений, для которого издержки меньше.
, объявить оптимальным то из этих двух значений, для которого издержки меньше.
Модель без дефицита - предельный случай для модели с дефицитом при безграничном возрастании платы за дефицит. В частности,

Как и в случае модели без дефицита, план с объемом поставки, определяемой по формуле квадратного корня,  , является асимптотически оптимальным.
, является асимптотически оптимальным.
Система моделей на основе модели Вильсона.Классическая модель теории управления запасами, называемая также моделью Вильсона, допускает различные обобщения.
Одно из таких обобщений - модель с конечной скоростью поставки 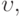 т. е. модель, в которой за время
т. е. модель, в которой за время  поставляется продукция объемом
поставляется продукция объемом  (при наличии в то же время постоянного спроса с интенсивностью
(при наличии в то же время постоянного спроса с интенсивностью 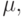 причем считается, что
причем считается, что  ). Таким образом, в этой модели поставка происходит не мгновенно, а в течение некоторого интервала времени, причем объем поставляемой продукции линейно зависит от времени. Такие поставки будем называть линейными с интенсивностью
). Таким образом, в этой модели поставка происходит не мгновенно, а в течение некоторого интервала времени, причем объем поставляемой продукции линейно зависит от времени. Такие поставки будем называть линейными с интенсивностью 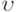 .
.
Другое обобщение классической модели связано с обобщением функции от объема запаса, задающей плату за хранение. В исходной модели считалось, что расходы за хранение пропорциональны объему продукции на складе. Естественно считать, что эти расходы должны содержать постоянный член  , не зависящий от объема продукции на складе (расходы на содержание самого склада, оплату работников и т. д.). Однако оптимальный план при таком обобщении не изменится. Действительно, в формуле для издержек добавится постоянный член
, не зависящий от объема продукции на складе (расходы на содержание самого склада, оплату работников и т. д.). Однако оптимальный план при таком обобщении не изменится. Действительно, в формуле для издержек добавится постоянный член  , и положение минимума не изменится при его добавлении.
, и положение минимума не изменится при его добавлении.
Однако в модели с дефицитом ситуация иная. Затраты на хранение возникают только при наличии товара на складе, и издержки этого вида вполне естественно разделить на постоянные и переменные (пропорциональные объему запаса на складе).
Аналогично издержки, вызванные дефицитом, вполне естественно разделить на постоянные (вызванные самим фактом дефицита) и переменные (пропорциональные величине дефицита).
В классической модели плата за доставку партии не зависит от объема партии. Т. е. здесь используются только постоянные издержки. Представляется вполне естественным ввести линейный член, соответствующий возрастанию платы за доставку в зависимости от величины партии (переменные издержки). (Ниже будет показано, что добавление этого члена не влияет на решение задачи оптимизации и вид оптимального плана.) Дальнейшее обобщение - введение скидок в зависимости от величины партии. Это приводит к выражению платы за доставку в виде квадратного трехчлена от объема партии.
Можно рассматривать одновременно несколько обобщений. В результате получаем систему моделей на основе классической модели управления запасами, состоящую из 36 моделей [12]. Каждая из них может быть описана набором четырех чисел ( 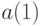 ,
, 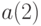 ,
, 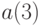 ,
, 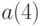 ). Каждое из этих чисел соответствует одному из рассмотренных выше видов обобщений исходной модели.
). Каждое из этих чисел соответствует одному из рассмотренных выше видов обобщений исходной модели.
При этом 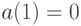 , если поставки мгновенные, и
, если поставки мгновенные, и 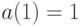 , если поставки являются линейными с интенсивностью
, если поставки являются линейными с интенсивностью 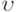 , причем
, причем 
Если плата за хранение продукции объемом  в течение единицы времени равна
в течение единицы времени равна 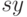 , то
, то 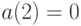 . Если же учтены постоянные (при наличии товара на складе) издержки, т. е. указанная плата равна
. Если же учтены постоянные (при наличии товара на складе) издержки, т. е. указанная плата равна  ,
,  , то
, то 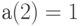 .
.
Если плата за нехватку продукции объемом  в течение единицы времени бесконечна (т. е. дефицит не допускается), то
в течение единицы времени бесконечна (т. е. дефицит не допускается), то 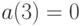 . Если эта плата равна
. Если эта плата равна 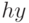 (рассмотренная выше модель с дефицитом), то
(рассмотренная выше модель с дефицитом), то 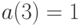 . Если же вводятся также постоянные издержки (плата за само наличие дефицита), т. е. плата за нехватку продукции объемом
. Если же вводятся также постоянные издержки (плата за само наличие дефицита), т. е. плата за нехватку продукции объемом  в течение единицы времени равна
в течение единицы времени равна 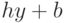 ,
, 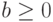 , то
, то 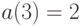 .
.
Наконец, 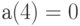 , если плата за доставку партии продукции объемом
, если плата за доставку партии продукции объемом  равна
равна  . Если учитываются переменные издержки, т. е. эта плата равна
. Если учитываются переменные издержки, т. е. эта плата равна 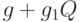 , то
, то 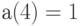 . Если же в модели учитываются скидки на объем партии, т.е. если плата за доставку партии продукции объемом
. Если же в модели учитываются скидки на объем партии, т.е. если плата за доставку партии продукции объемом  равна
равна 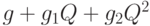 , то
, то 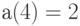 .
.
Для 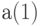 имеется два возможных значения, для
имеется два возможных значения, для 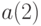 - тоже два, для
- тоже два, для 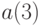 - три возможных значения, для
- три возможных значения, для 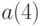 - тоже три. Всего имеется
- тоже три. Всего имеется  возможных комбинаций, т. е. 36 возможных моделей. Классическая модель управления запасами описывается набором
возможных комбинаций, т. е. 36 возможных моделей. Классическая модель управления запасами описывается набором 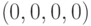 , а модель с дефицитом - набором
, а модель с дефицитом - набором 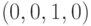 .
.
Рассмотрим наиболее обобщенную модель рассматриваемой системы. Она описывается набором 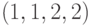 . Можно показать, что для нее справедливы основные утверждения, касающиеся классической модели и модели с дефицитом. Однако "формула квадратного корня" имеет более сложный вид, а именно,
. Можно показать, что для нее справедливы основные утверждения, касающиеся классической модели и модели с дефицитом. Однако "формула квадратного корня" имеет более сложный вид, а именно,
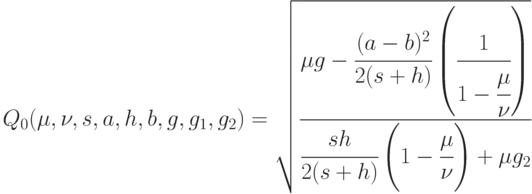
В частности, план с 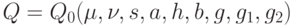 асимптотически оптимальный.
асимптотически оптимальный.
Формула для 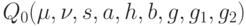 позволяет обнаружить ряд любопытных эффектов. Так, в ней не участвует параметр
позволяет обнаружить ряд любопытных эффектов. Так, в ней не участвует параметр 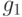 . Другими словами, при любом изменении этого параметра оптимальный объем поставки не меняется. Если запас пополняется весьма быстро по сравнению со спросом, т. е.
. Другими словами, при любом изменении этого параметра оптимальный объем поставки не меняется. Если запас пополняется весьма быстро по сравнению со спросом, т. е.  то соответствующий множитель в "формуле квадратного корня" исчезает, и для моделей с
то соответствующий множитель в "формуле квадратного корня" исчезает, и для моделей с 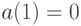 получаем более простую формулу
получаем более простую формулу
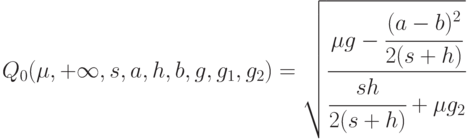
Дальнейшее упрощение получаем при 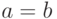 . Это равенство означает, что постоянные (в другой терминологии - фиксированные) платежи за хранение и в связи с дефицитом совпадают, например, равны 0. Если последнее утверждение справедливо, то
. Это равенство означает, что постоянные (в другой терминологии - фиксированные) платежи за хранение и в связи с дефицитом совпадают, например, равны 0. Если последнее утверждение справедливо, то
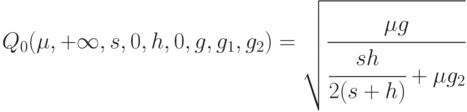
Предположим теперь, что при доставке партии отсутствуют скидки (или надбавки) за размер партии. Тогда "формула квадратного корня" упрощается дальше и приобретает вид
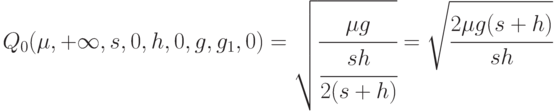
Эта формула уже получена выше при рассмотрении модели с дефицитом. При безграничном возрастании  получаем формулу Вильсона для классической модели управления запасами:
получаем формулу Вильсона для классической модели управления запасами:
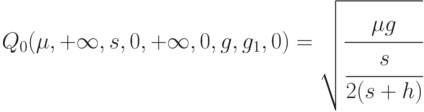
Новое в последних двух формулах - наличие в левой части параметра 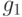 , не участвующего в формировании объема партии.
, не участвующего в формировании объема партии.
Важное замечание 3.Модели конкретных экономических (и не только) процессов и явлений обычно не встречаются и не изучаются поодиночке. Обычно имеется совокупность моделей, объединенных в систему, переходящих друг в друга при тех или иных предельных переходах. Часто более простые модели используются для расчетов, более сложные применяются для изучения точности, достигаемой с помощью более простых, согласно подходу, развитому в [13, 11].