|
"...Изучение и анализ примеров.
В и приведены описания и приложены исходные коды параллельных программ..." Непонятно что такое - "В и приведены описания" и где именно приведены и приложены исходные коды. |
Решето Эратосфена для нахождения простых чисел
Рассмотрим задачу отыскания всех простых чисел в интервале от 2 до некоторого заданного числа  . Выделим в исходном списке
. Выделим в исходном списке  первое число, которое будет простым, и затем зачеркнем как само число 2, так и все числа в списке, кратные ему. Чтобы зачеркнуть эти кратные числа, достаточно зачеркнуть каждое второе число в списке, начиная с числа 2. Затем выделяем первое незачеркнутое число в качестве очередного простого - им будет число 3, и проводим аналогичную процедуру, зачеркивая каждое третье число, начиная с числа 3. Продолжаем эту процедуру до тех пор, пока не дойдем до очередного простого числа
первое число, которое будет простым, и затем зачеркнем как само число 2, так и все числа в списке, кратные ему. Чтобы зачеркнуть эти кратные числа, достаточно зачеркнуть каждое второе число в списке, начиная с числа 2. Затем выделяем первое незачеркнутое число в качестве очередного простого - им будет число 3, и проводим аналогичную процедуру, зачеркивая каждое третье число, начиная с числа 3. Продолжаем эту процедуру до тех пор, пока не дойдем до очередного простого числа  , такого что
, такого что  . Легко видеть, что все оставшиеся незачеркнутыми числа в интервале
. Легко видеть, что все оставшиеся незачеркнутыми числа в интервале  являются простыми. Описанный метод нахождения простых чисел носит название решета Эратосфена.
являются простыми. Описанный метод нахождения простых чисел носит название решета Эратосфена.
В этом разделе будет описан параллельный вариант алгоритма решета Эратосфена (http://software.intel.com/en-us/articles/parallel-reduce/ ), взятый из примеров к библиотеке Intel Threading Building Blocks ( http://www.threadingbuildingblocks.org/), и реализованный с использованием средств библиотеки PFX.
Параллельный алгоритм поиска простых чисел на основе решета Эратосфена
Будем рассматривать задачу нахождения количества простых чисел в интервале от 2 до  (
(  ). (В действительности, в программе будет иметься специальный ключ, задание которого будет приводить также к распечатке всех найденных простых чисел).
). (В действительности, в программе будет иметься специальный ключ, задание которого будет приводить также к распечатке всех найденных простых чисел).
Идея алгоритма состоит в разбиении поиска на 2 этапа: на 1-ом этапе, который выполняется последовательно, находятся все простые числа в диапазоне 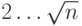 с помощью классического метода решета Эратосфена. Найденные простые числа, на 2-ом этапе, позволяют вычеркнуть все составные числа в диапазоне
с помощью классического метода решета Эратосфена. Найденные простые числа, на 2-ом этапе, позволяют вычеркнуть все составные числа в диапазоне 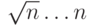 . Параллелизация заключается в том, что диапазон
. Параллелизация заключается в том, что диапазон 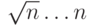 разбивается на поддиапазоны размера
разбивается на поддиапазоны размера  , где
, где 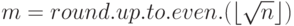 , в которых поиск простых чисел может происходить независимо.
, в которых поиск простых чисел может происходить независимо.
В приведенном ниже алгоритме учитываются также следующие свойства задачи:
- поскольку все четные числа, за исключением числа 2, являются составными, то в каждом поддиапазоне размера
 рассматриваются только нечетные числа; следствием этого является то, что размер соответствующих массивов равен
рассматриваются только нечетные числа; следствием этого является то, что размер соответствующих массивов равен 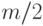 ;
; - в силу выбора размера диапазона равным
 , количество поддиапазонов, рассматриваемых на 2-ом этапе, также не будет превышать
, количество поддиапазонов, рассматриваемых на 2-ом этапе, также не будет превышать  , что, одновременно, является верхней границей максимального числа потоков для обработки.
, что, одновременно, является верхней границей максимального числа потоков для обработки.
Описание 1-ой стадии
Назначение первой стадии ? отыскать все простые числа в поддиапазоне 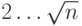 , которые затем будут использоваться для нахождения простых чисел в следующих поддиапазонах.
, которые затем будут использоваться для нахождения простых чисел в следующих поддиапазонах.
В начале 1-ой стадии, размещаются массивы is_composite и prime_steps размерности 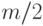 , где первый массив служит для процедуры просеивания, а во втором массиве сохраняются найденный на этой стадии простые числа. В массиве is-composite элемент с номером
, где первый массив служит для процедуры просеивания, а во втором массиве сохраняются найденный на этой стадии простые числа. В массиве is-composite элемент с номером  соответствует нечетному числу
соответствует нечетному числу 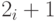 . Сам алгоритм состоит в обычном просеивании Эратосфена, начиная с элемента массива is_composite с номером
. Сам алгоритм состоит в обычном просеивании Эратосфена, начиная с элемента массива is_composite с номером 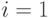 , т.е., простого числа 3 (простое число 2 учитывается специальным образом).
, т.е., простого числа 3 (простое число 2 учитывается специальным образом).
Описание 2-ой стадии
Вторая стадия алгоритма заключается в одновременной обработке  поддиапазонов, укладывающихся в интервале
поддиапазонов, укладывающихся в интервале 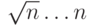 , с помощью нескольких потоков.
, с помощью нескольких потоков.
Каждый поток, в общем случае, обрабатывает несколько поддиапазонов, сохраняя количество найденных в них простых чисел в соответствующем элементе массива count_primes. После окончания работы всех потоков (т.е., после выхода из цикла Parallel.For), находится сумма всех элементов массива count_primes, которая добавляется к количеству найденных простых чисел на первом этапе. Это значение - totalCountPrimes и становится результатом решения задачи.
Ключевым моментом 2-ой стадии является обработка потоком одного поддиапазона, начинающегося с числа start, и имеющего размер  . Для начала непосредственного просеивания в этом поддиапазоне, необходимо для каждого простого числа
. Для начала непосредственного просеивания в этом поддиапазоне, необходимо для каждого простого числа  , найденного на первой стадии, вычислить смещение от начала данного поддиапазона ? т.е., позицию, начиная с которой будет происходить зачеркивание чисел с определенным шагом, равным
, найденного на первой стадии, вычислить смещение от начала данного поддиапазона ? т.е., позицию, начиная с которой будет происходить зачеркивание чисел с определенным шагом, равным  .
.
Вычисление данного смещения содержательно можно разбить на 4 шага:
- определяем число, на котором "остановился" процесс зачеркивания в предыдущем поддиапазоне для данного
 ; это число определяется по формуле
; это число определяется по формуле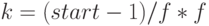
- так как все поддиапазоны, в том числе и предыдущий, имеют размер
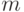 , то от начала этого поддиапазона число
, то от начала этого поддиапазона число  отстоит на расстоянии
отстоит на расстоянии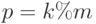
-
поскольку в каждом поддиапазоне проверяются на простоту только нечетные числа, то позиция (отсчитываемая от начала предыдущего поддиапазона) следующего нечетного числа (т.е., числа с которого начнется просеивание в текущем поддиапазоне) определяется как
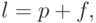 если
если  четно,
четно,и
 , если
, если  нечетно
нечетно - наконец, определяем позицию относительно данного поддиапазона полученного на предыдущем шаге нечетного числа, учитывая, что в поддиапазоне рассматриваются только нечетные числа:
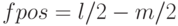
Рассмотрим пример вычисления смещения в соответствии с шагами, представленными выше.
Пусть 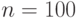 , тогда
, тогда  , и простыми числами, найденными в первом поддиапазоне, являются 3,5,7.
, и простыми числами, найденными в первом поддиапазоне, являются 3,5,7.
Рассмотрим, допустим, третий по счету поддиапазон, задаваемый, соответственно параметрами 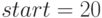 и
и 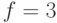 . Тогда
. Тогда
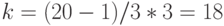
Т.е., последнее число, кратное 3, в предыдущем поддиапазоне есть число 18, которое отстоит от начала предыдущего поддиапазона на расстоянии

Т.к.  четно, то позиция следующего нечетного числа определяется как
четно, то позиция следующего нечетного числа определяется как
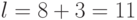
(легко заметить, что эта позиция соответствует числу 21). Тогда, число 21, с которого мы начнем зачеркивание чисел в третьем поддиапазоне с шагом 3, имеет смещение относительно начала этого диапазона
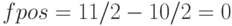
Действительно, число 21 является первым нечетным числом в 3-ем поддиапазоне, а потому оно имеет смещение 0 от начала этого поддиапазона.
