|
"...Изучение и анализ примеров.
В и приведены описания и приложены исходные коды параллельных программ..." Непонятно что такое - "В и приведены описания" и где именно приведены и приложены исходные коды. |
Опубликован: 15.10.2009 | Доступ: свободный | Студентов: 903 / 252 | Оценка: 4.42 / 4.20 | Длительность: 08:22:00
Специальности: Программист
Лекция 11:
Решето Эратосфена для нахождения простых чисел
11.2 Реализация с использованием PFX
Обязательными входными параметрами программы являются:  - верхняя граница диапазона, в котором ищутся простые числа;
- верхняя граница диапазона, в котором ищутся простые числа;  - количество потоков. Необязательным третьим параметром является ключ
- количество потоков. Необязательным третьим параметром является ключ  , задающим печать всех найденных простых чисел. Базовой функцией программы является функция ParallelCountPrimes, входными параметрами которой являются
, задающим печать всех найденных простых чисел. Базовой функцией программы является функция ParallelCountPrimes, входными параметрами которой являются  и
и  , а возвращаемым значением - количество простых чисел в интервале
, а возвращаемым значением - количество простых чисел в интервале 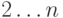 .
.
Полный текст программы с комментариями приведен ниже.
//Программа реализует алгоритм поиска простых чисел, подобный алгоримту,
//реализованному в примерах библиотеки Intel TBB (tbb21_20080605).
using System;
using System.Collections.Generic;
using System.Text;
using System.Threading;
namespace Sieve
{
class Program
{
static bool PrintPrimes;
class Multiples
{
// хранит флаг простоты нечетного числа в данном поддиапазоне
private bool[] is_composite;
// простые числа найденные на первом этапе алгоритма
private int[] prime_steps;
//индекс в поддиапазоне is_composite, с которого нужно начать вычеркивание с шагом prime_steps[k]
private int[] to_strike;
// число найденных на первом этапе простых чисел
public int n_prime_steps;
public int m;
// Конструктор копирования
public Multiples(Multiples rhs)
{
prime_steps = new int[rhs.prime_steps.Length];
rhs.prime_steps.CopyTo(prime_steps, 0);
n_prime_steps = rhs.n_prime_steps;
m = rhs.m;
}
public Multiples(int n)
{
m = (int)Math.Sqrt(n);
m += m&1;
// Для работы алгоритма требуется меньшее или равное m/2 = (|_sqrt(n)_|)/2 количество ячеек в массиве
// так как:
// 1) ищутся только простые числа, меньшие либо равные sqrt(n)
// 2) простых чисел не может быть больше половины всех чисел (т.к. каждое второе число четное)
is_composite = new bool[m/2];
prime_steps = new int[m/2];
n_prime_steps = 0;
// найдем все простые числа меньшие m: m=to_even(sqrt(n))
// перебираем все нечетные числа в поддиапазоне [3;m-1]
// (т.к. четные числа автоматически вычеркнуты)
for (int i = 3; i<= m; i += 2)
{
//если число ранее не было признано составным (т.е. это число простое)
if( !is_composite[i/2] )
{
if( PrintPrimes ) Console.WriteLine(i);
// с шагом равному простому числу перемещаемся по интервалу [простое число/2; m/2]
// в результате вычеркнем все числа, делящиеся на простое число i (модифицируем массив is_composite)
strike( i/2, m/2, i );
// запомним шаг\новое простое число
prime_steps[n_prime_steps++] = i;
}
}
}
// Процедура strike вычеркивает составные числа в интервале [start;limit) с шагом step.
// Возвращает значение limit%step==0? limit: limit-step.
int strike(int start, int limit, int step)
{
for (; start<= limit; start += step)
is_composite[start] = true;
return start;
}
// Поиск простых чисел в пддиапазоне [start,window_size).
Возвращает число найденных простых чисел
// В процессе работы изменяет массив to_strike
public int find_primes_in_window( int start, int window_size )
{
for( uint k=0; kle;n_prime_steps; ++k )
to_strike[k] = strike( to_strike[k]-m/2, window_size/2, prime_steps[k] );
int count = 0;
for( int k=0; kle;window_size/2; ++k )
{
if (!is_composite[k])
{
if( PrintPrimes ) Console.WriteLine(start+2*k+1);
//нашли простое число, увеличим счетчик на 1
count=count+1;
}
}
return count;
}
// Функция расчета смещений для каждого шага (простого числа).
Смещения указываются от начала поддиапазона
public void initialize(int start)
{
is_composite = new bool[m / 2];
to_strike = new int[m / 2];
for (uint k = 0; k<= n_prime_steps; ++k)
{
// выберем простое число f (шаг)
int f = prime_steps[k];
// p - расстояние от начала предыдущего поддиапазона,
на котором остановилось вычеркивание с данным шагом f
int p = (start - 1) / f * f % m;
to_strike[k] = (Convert.ToBoolean(p &1) - p + 2 * f : p + f) / 2;
}
}
}
class Sieve
{
public Multiples multiples;
// Число простых чисел, найденных данным решетом
public int count = 0;
// Конструктор копирования
public Sieve(Sieve rhs)
{
multiples = new Multiples(rhs.multiples);
}
public Sieve( int n )
{
multiples = new Multiples(n);
}
// Поиск простых чисел в подиапазоне [start;start+window_size]
public int calc(int start, int window_size, int n)
{
// вычисляем начальные смещения для данного поддиапазона (для всех шагов)
multiples.initialize(start);
int tt = window_size;
// контролируем выход за границы общего диапазона
if (start + window_size > n)
tt = n - start;
// ищем простые числа в данном поддиапазоне
return multiples.find_primes_in_window(start, tt);
}
// Поиск простых чисел в интервале для данного потока
public int ThreadSieving(int window_size, int start, int fin, int n)
{
Sieve s1 = new Sieve(this);
int count_primes = 0;
for (int j = start; j<= fin; j += window_size)
count_primes += s1.calc(j, window_size, n);
return count_primes;
}
}
public static int ParallelCountPrimes(int n, ref int p)
{
// учтем число 2
totalCountPrimes++;
if( n>=3 )
{
// создание решета включает в себя первый этап алгоритма - поиск шагов
Sieve s = new Sieve(n);
// размер поддиапазона
int window_size = s.multiples.m;
// запомним количество простых чисел, найденных на первом этапе
totalCountPrimes=totalCountPrimes+s.multiples.n_prime_steps;
int threads = p;
if(p>window_size)
{
Console.WriteLine("Warning: Threads number ( "+p+" ) can't be greater
then Window Size ( "+window_size+" );");
p=window_size;
threads = p;
Console.WriteLine("Warning: Threads number set to "+window_size+" ;");
}
// массив с числом простых чисел, найденных каждым потоком
int[] count_primes = new int[threads];
// целое количество поддиапазонов в рассматриваемом диапазоне [2..n)
// первый поддиапазон был обработан при создании решета s
int windows_n = (n / window_size)-1;
// остаток элементов
int modn = n % window_size;
// целое количество поддиапазонов, приходящихся на один поток
int q = windows_n / threads;
// оставшиеся число поддиапазонов
int r = windows_n % threads;
// второй этап алгоритма - параллельный поиск простых чисел по поддиапазонам
Parallel.For(0, threads, i =>
{
// начало интервала (интервал состоит из нескольких поддиапазонов)
int start;
// конец интервала
int fin;
if (i<= r)
{
start = i * (q + 1) + 1;
fin = start + q + 1;
}
else
{
start = (r * (q + 1) + (i - r) * q) + 1;
fin = start + q;
}
if (i != threads - 1)
count_primes[i] = s.ThreadSieving(window_size, start * window_size, fin * window_size, n);
else
count_primes[i] = s.ThreadSieving(window_size, start * window_size, fin * window_size + modn, n);
});
// определим общее количество найденных простых чисел
for (int i = 0; i<= threads; i++)
totalCountPrimes += count_primes[i];
}
return totalCountPrimes;
}
// общее число найденных простых чисел в интервале [2..n)
static int totalCountPrimes = 0;
static void Main(string[] args)
{
// кол-во чисел
int n = 0;
// число потоков; число потоков не может быть больше window_size
int p = 0;
try
{
if (args.Length >== 2)
{
// алгоритм расчитан на работу с открытым справа интервалом [2...n)
n = Convert.ToInt32(args[0]);
p = Convert.ToInt32(args[1]);
if (args.Length >== 3)
PrintPrimes = args[2] == "verb";
}
else { Console.WriteLine(Usage()); return; }
}
catch (Exception e) { Console.WriteLine(Usage()); return; }
Console.WriteLine("#primes from [2.." + n + ") = " + totalCountPrimes +
" (" + (dt2 - dt1).TotalSeconds + " sec with " + p + "-threads)");
}
static string Usage()
{
string pname = System.Reflection.Assembly.GetEntryAssembly().GetName().Name;
StringBuilder s = new StringBuilder();
for (int i = 0; i<= Console.WindowWidth; i++) s.Append("-");
return (s.ToString() + Environment.NewLine +
"Usage: " + pname + " n p [verb]" + Environment.NewLine +
"where" + Environment.NewLine +
" n - upper excluded bound of interval [2...n)" + Environment.NewLine +
" p - threads number" + Environment.NewLine +
" verb - verbosity" + Environment.NewLine +
s.ToString() + Environment.NewLine);
}
}
}