НОУ ИНТУИТ | Параллельное программирование для многоядерных процессоров. Лекция 12: Параллельный алгоритм дискретного преобразования Фурье

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 15.10.2009 | Доступ: свободный | Студентов: 896 / 248 | Оценка: 4.42 / 4.20 | Длительность: 08:22:00

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 7 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В этой лекции рассмотрена теория и реализация алгоритма дискретного преобразования Фурье в контексте параллельного программирования.

Ключевые слова: вектор, вычисление, алгоритм, распараллеливание, выражение, блок-схема, последовательный алгоритм, двумерный массив, базовая, функция, множитель, транспонирование, parallelize

Напомним коротко основные понятия и определения, относящиеся к дискретному предобразованию Фурье (ДПФ). Более подробно об этом см., например, в главе 1 книги [ [ 4 ] ].

Пусть 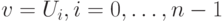$v={U_i,i=0,\dots,n-1}$ является вектором с вещественными или комплексными компонентами. Дискретным преобразованием Фурье вектора называется вектор 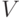длины с комплексными компонентами, определяемыми равенствами:

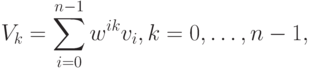$\label{travial}V_k=\sum_{i=0}^{n-1}w^{ik}v_i,k=0,\dots,n-1,$

( 1)

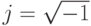где $w=e^{-j2pi/n}$ и $j=\sqrt{-1}$ .

Вычисление преобразования Фурье в виде (1), как оно записано выше, требует порядка 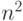n^2 умножений и 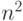n^2 сложений.

В книге [ [ 5 ] ], раздел 32.3, приведен алгоритм вычисления ДПФ, требующий порядка 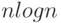n log n операций, и потому названный алгоритмом быстрого преобразования Фурье (БПФ). Однако, этот алгоритм трудно поддается распараллеливанию, а потому, используя его, трудно получить дальнейшее снижение сложности алгоритма БПФ.

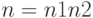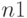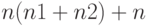Однако, существует другой алгоритм - так называемый алгоритм Кули-Тьюки (книга [ [ 4 ] ], глава 4), который применим когда число является составным. В частности, если n = n1 n2 для некоторых и , то алгоритм Кули-Тьюки требует порядка n(n1+n2)+n умножений, но который эффективно параллелится. Особенности параллельной реализации алгоритма Кули-Тьюки состоят в том, что

входной и выходной векторы рассматриваются как двумерные таблицы, столбцы и строки которых могут обрабатываться независимо в различных потоках,
в рамках одного потока, обработка отдельных столбцов и строк представляет собой вычисление ДПФ с помощью алгоритма БПФ.

Суть алгоритма Кули-Тьюки (дополнительные подробности см. в книге [ [ 4 ] ], глава 4) состоит в преобразовании выражения ~(\ref{travial}) в соответствии со следующими равенствами для индексов и :

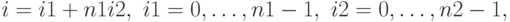
$i = i1 + n1 i2,~i1 = 0, \dots , n1 -1,~ i2 = 0, \dots , n2 - 1,$

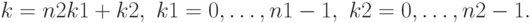
$k = n2 k1 + k2,~ k1 = 0, \dots, n1 - 1,~ k2 = 0, \dots, n2 - 1.$

Тогда, выражение (1) может быть переписано в виде

$}\label{travial}V_k1,k2=\sum_{i1=0}^{n1-1}b^{i1k1}[w^{i1k2}\sum_{i2=0}^{n2-1}y^{i2k2}v_{i1i2}].$

( 2)

в котором

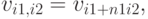
$v_{i1,i2} = v_{i1+n1i2},$

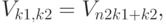
$V_{k1,k2} = V_{n2k1+k2},$

$\beta = \omega^{n2},$

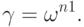
$\gamma = \omega^{n1}.$

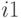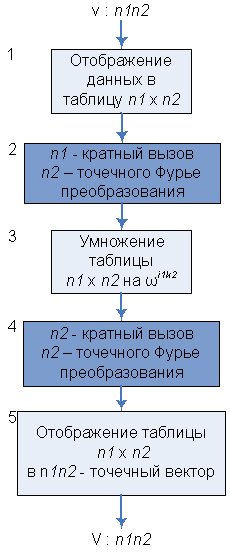
В этом выражении, при каждом значении внутренняя сумма представляет собой -точечное преобразование Фурье, а внешняя сумма есть 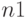-точечное преобразование Фурье. Соответственно, блок-схема последовательного алгоритма Кули-Тьюки может быть представлена следующим образом:

Заметим, что реального отображения исходного вектора в двумерный массив не происходит - эта операция заменяется соответствующим пересчетом индексов.

Ниже представлена базовая часть БПФ-алгоритма Кули-Тьюки, которая включает в себя 4 шага:

применение БПФ к каждому столбцу,
поэлементное умножение на $\omega^{i1k2}$ ,
построчное применение БПФ,
восстановление результирующего вектора из двумерной таблицы.

//    Cooley-Tukey Algorithm
    public Complex[] FFT(Complex[] X, int n1, int n2)
    {
        int n = X.Length;
        Complex[,] Y = new Complex[n1,n2];
        Complex[,] P = new Complex[n1,n2];
        Complex[] T = new Complex[n];


        for (int k = 0; k < n1; k++)
            ColumnFFT(X, Y, n1, n2 ,k);

        for (int k = 0; k < n1; k++)
            TwiddleFactorMult(Y, n1, n2, k);

        for (int i = 0; i < n2; i++)
            RowFFT(Y, P, i, n1);
        
        //Sort elements in right order to create output vector
        for (int j = 0; j < n2; j++)
            for (int i = 0; i < n1; i++)
                T[i * n2 + j] = P[i, j];

        return T;
}

Здесь, ColumnFFT и RowFFT - функции, осуществляющие БПФ для одного столбца и, соответственно, строки матрицы, функция TwiddleFactorMult - функция, осуществляющая домножение столбца матрицы на дополнительный множитель, а функция TL_idx реализует транспонирование линеаризованной таблицы.

Параллельная реализация БПФ-алгоритма Кули-Тьюки состоит из двух следующих друг за другом циклов Parallel.For, где в первом цикле выполняются шаги (1) и (2) последовательного алгоритма, а во втором цикле - шаги (3) и (4).

//    Cooley-Tukey Algorithm. Parallel Implementation
    public Complex[] FFT(Complex[] X, int n1, int n2)
    {
        int n = X.Length;
        Complex[,] Y = new Complex[n1, n2];
        Complex[,] P = new Complex[n1, n2];
        Complex[] T = new Complex[n];

        Parallel.For(0,n1,k= > {
            ColumnFFT(X, Y, n1, n2, k);
            TwiddleFactorMult(Y, n1, n2, k);
        });

        Parallel.For(0, n2, q = >
        {
            RowFFT(Y, P, q, n1);
            //Sort elements in right order to create output vector
            for (int i = 0; i < n1; i++)
                T[i * n2 + q] = P[i, q];
        });

        return T;
    }

Полностью код параллельной версии БПФ-алгоритма Кули-Тьюки приведен ниже:

//PFX Parallel Fast Fourier Transform (pFFT)
//This implementation is based on the Cooley-Tukey algorithm

using System;
using System.Text;
using System.Threading;

public class Complex
{
    public double Re = 0.0;
    public double Im = 0.0;

    public Complex() { }
    public Complex(double re, double im) { Re = re; Im = im; }
    public override string ToString()
    {
        return Re + " " + Im;
    }
}

class Program
{
    public static void Main(string[] args)
    {
        if (args.Length != 3)
        {
            Console.WriteLine(Usage());
            return;
        }

        //n - input vector length (must be power of two)
        //n1 - number of Cooley-Tukey's matrix columns
        //n2 - number of Cooley-Tukey's matrix rows

        int n = 0, n1 = 0, n2 = 0;
        n = (int)Math.Pow(2, Int32.Parse(args[0]));
        n1 = Int32.Parse(args[1]);

        //input vector generation
        Complex[] X = new Complex[n];
        Random r = new Random();
        for (int i = 0; i < n; i++)
            X[i] = new Complex(r.NextDouble() * 10, 0);

        if ((n1 > n) || (n1 < = 0))
        {
            Console.WriteLine(Usage() + " Param n1 is invalid: n1= " + n1.ToString() + ". Vector length= " + X.Length.ToString());
            return;
        }

        n2 = n / n1;

        Console.WriteLine("*RUN*");

        DateTime dt1 = DateTime.Now;
        Complex[] pY = (new Program()).FFT(X, n1, n2);
        DateTime dt2 = DateTime.Now;

        Console.WriteLine(" Parallel FFT: ");
        Console.WriteLine(" n= " + n + " n1= " + n1 + " n2= " + n2 +
              "   Elapsed time is " + (dt2 - dt1).TotalSeconds);
    }

    //    Cooley-Tukey Algorithm. Parallel Implementation
    public Complex[] FFT(Complex[] X, int n1, int n2)
    {
        int n = X.Length;
        Complex[,] Y = new Complex[n1, n2];
        Complex[,] P = new Complex[n1, n2];
        Complex[] T = new Complex[n];

        Parallel.For(0,n1,k= > {
            ColumnFFT(X, Y, n1, n2, k);
            TwiddleFactorMult(Y, n1, n2, k);
        });

        Parallel.For(0, n2, q = >
        {
            RowFFT(Y, P, q, n1);
            //Sort elements in right order to create output vector
            for (int i = 0; i < n1; i++)
                T[i * n2 + q] = P[i, q];
        });

        return T;
    }

    private void TwiddleFactorMult(Complex[,] Y, int n1, int n2, int k)
    {
        //Column Twiddle Factor Multiplication
        double wn_Re = 0, arg = 0, wn_Im = 0, tmp = 0;
        for (int q = 0; q < n2; q++)
        {
            arg = 2 * Math.PI * k * q / (n2 * n1);
            wn_Re = Math.Cos(arg);
            wn_Im = Math.Sin(arg);

            tmp = Y[k, q].Re * wn_Re - Y[k, q].Im * wn_Im;
            Y[k, q].Im = Y[k, q].Re * wn_Im + Y[k, q].Im * wn_Re;
            Y[k, q].Re = tmp;
        }
    }

    public void ColumnFFT(Complex[] a, Complex[,] A, int n1, int n2, int k)
    {
        int q, m, m2, s;
        double wn_Re, wn_Im, w_Re, w_Im;
        double arg, t_Re, t_Im;
        double u_Re, u_Im, tmp;

        int logN = 0;
        m = n2;

        while (m > 1)
        {
            m = m / 2;
            logN++;
        }

        int temp;
        for (q = 0; q < n2; q++)
        {
            temp = bit_reverse(q, logN);
            A[k, temp] = a[k + q * n1];
        }

        for (s = 1; s < = logN; s++)
        {
            m = 1 < < s;

            arg = 2.0 * Math.PI / m;

            wn_Re = Math.Cos(arg);
            wn_Im = Math.Sin(arg);

            w_Re = 1.0; w_Im = 0.0;

            m2 = m > > 1;
            for (int i = 0; i < m2; i++)
            {
                for (int j = i; j < n2; j += m)
                {
                    t_Re = w_Re * A[k, j + m2].Re - w_Im * A[k, j + m2].Im;
                    t_Im = w_Re * A[k, j + m2].Im + w_Im * A[k, j + m2].Re;

                    u_Re = A[k, j].Re;
                    u_Im = A[k, j].Im;

                    A[k, j].Re = u_Re + t_Re;
                    A[k, j].Im = u_Im + t_Im;

                    A[k, j + m2].Re = u_Re - t_Re;
                    A[k, j + m2].Im = u_Im - t_Im;
                }
                tmp = w_Re * wn_Re - w_Im * wn_Im;
                w_Im = w_Re * wn_Im + w_Im * wn_Re;
                w_Re = tmp;
            }

        }

    }

    public void RowFFT(Complex[,] a, Complex[,] A, int q, int n1)
    {
        int j, k, m, m2, s;
        double wn_Re, wn_Im, w_Re, w_Im;
        double arg, t_Re, t_Im;
        double u_Re, u_Im, tmp;

        int logN = 0;
        m = n1;
        while (m > 1)
        {
            m = m / 2;
            logN++;
        }

        for (k = 0; k < n1; k++)
            A[bit_reverse(k, logN), q] = a[k, q];

        for (s = 1; s < = logN; s++)
        {
            m = 1 < < s;

            arg = 2.0 * Math.PI / m;

            wn_Re = Math.Cos(arg);
            wn_Im = Math.Sin(arg);

            w_Re = 1.0; w_Im = 0.0;

            m2 = m > > 1;
            for (j = 0; j < m2; j++)
            {
                for (k = j; k <= n1; k += m)
                {
                    t_Re = w_Re * A[k + m2, q].Re - w_Im * A[k + m2, q].Im;
                    t_Im = w_Re * A[k + m2, q].Im + w_Im * A[k + m2, q].Re;

                    u_Re = A[k, q].Re;
                    u_Im = A[k, q].Im;

                    A[k, q].Re = u_Re + t_Re;
                    A[k, q].Im = u_Im + t_Im;

                    A[k + m2, q].Re = u_Re - t_Re;
                    A[k + m2, q].Im = u_Im - t_Im;
                }

                tmp = w_Re * wn_Re - w_Im * wn_Im;
                w_Im = w_Re * wn_Im + w_Im * wn_Re;
                w_Re = tmp;
            }
        }
    }

    public int bit_reverse(int k, int size)
    {
        int right_unit = 1;
        int left_unit = 1 < < (size - 1);

        int result = 0, bit;

        for (int i = 0; i < size; i++)
        {
            bit = k & right_unit;
            if (bit != 0)
                result = result | left_unit;
            right_unit = right_unit < < 1;
            left_unit = left_unit > > 1;
        }
        return (result);
    }

    static string Usage()
    {
        string pname = System.Reflection.Assembly.GetEntryAssembly().GetName().Name;
        StringBuilder s = new StringBuilder();
        for (int i = 0; i < Console.WindowWidth; i++) s.Append(" - ");
        return (s.ToString() + Environment.NewLine +
              " Usage: " + pname + " p n1 np " + Environment.NewLine +
                      " where " + Environment.NewLine +
                      " p -  n=2^p - input vector length " + Environment.NewLine +
                      " n1 - width of block " + Environment.NewLine +
                     " np - number of processes " + Environment.NewLine +
                     s.ToString() + Environment.NewLine);
    }
}

Дальше >>

Авторизоваться

Параллельное программирование для многоядерных процессоров

Параллельный алгоритм дискретного преобразования Фурье

Вопросы и ответы