НОУ ИНТУИТ | Введение в XNA. Лекция 5: Вершинные шейдеры

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.04.2009 | Доступ: свободный | Студентов: 1840 / 107 | Оценка: 4.36 / 4.40 | Длительность: 16:40:00

Темы: Компьютерная графика, Программирование, Игры

Специальности: Программист

|

Вам нравится? Нравится 35 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Полноценный эффект

Отладив прототип эффекта можно приступать к реализации настоящего полноценного эффекта на языке HLSL. Используя в качестве шпаргалки листинг 5.9, написание вершинного шейдера не составит труда. Все что от нас требуется - убрать цикл перебора вершин и привести синтаксис в соответствии языку HLSL (листинг 5.11).

// Файл Disk.fx float angle;
struct VertexInput 
{
float3 pos : POSITION;
float4 color : COLOR; 
};
struct VertexOutput 
{
float4 pos : POSITION;
float4 color : COLOR; 
};
VertexOutput MainVS(VertexInput input) 
{
VertexOutput output;
float a = input.pos.y + angle;
output.pos.xy = input.pos.xx * float2(sin(a), cos(a));
output.pos.zw = float2(0.0, 1.0);
output.color = input.color;
return output; }
float4 MainPS(float4 color:COLOR):COLOR 
{
return color; 
}
technique Disk 
{
pass p0
{
VertexShader = compile vs11 MainVS(); PixelShader 
= compile ps11 MainPS();
} }

Листинг 5.11.

Преобразование приложения тоже выполняется тривиально и сводится к удалению вспомогательного кода, эмулирующего вершинный шейдер: необходимо убрать ставшие ненужными класс DiskEffect и массив вершин, обработанных вершинным шейдером ( transformedDiskVertices ). А угол поворота теперь должен присваиваться непосредственно параметру эффекта angle. Основные фрагменты обновленного приложения приведены в листинге 5.12.

public partial class MainForm : Form
{
// Используем новый эффект
const string effectFileName = "Data\\Disk.fx";
Effect diskEffect = null; 
// Объект EffectParameter, инкапсулирующий параметр 
эффекта angle EffectParameter 
angleParam = null;
private void MainForm_Load(object sender, EventArgs e) 
{ ...
// Получаем объект EffectParameter, соответствующий 
параметру эффекта angle angleParam = 
diskEffect.Parameters["angle"];
Debug.Assert(angleParam != null, effectFileName + " : 
не найден параметр angle"); 
}
private void MainForm_Paint(object sender, PaintEventArgs e)
{ ...
float time = (float)stopwatch.ElapsedTicks / 
(float)Stopwatch.Frequency; 
// Присваиваем угол поворота параметру angle эффекта
angleParam.SetValue(diskSpeed * time);
// Выполняем обычную визуализацию примитива
device.VertexDeclaration = diskDeclaration;
diskEffect.Begin();
for (int i = 0; i < diskEffect.CurrentTechnique.Passes.Count; i++)
{
EffectPass currentPass = diskEffect.CurrentTechnique.Passes[i];
currentPass.Begin();
device.DrawUserPrimitives(PrimitiveType.TriangleFan, 
diskVertices, 0, diskVertices.Length – 
2);
currentPass.End(); 
} diskEffect.End();
device.Present(); ...
} }

Листинг 5.12.

Как видно, обработчик события Paint лишь вычисляет новый угол поворота вершины и передает его в параметр эффекта шейдера. Собственно вращение вершин диска осуществляется только силами вершинного шейдера без какой-либо помощи со стороны C#- кода.

Анализ ассемблерного кода вершинного шейдера

Закончив создание эффекта самое время ознакомиться с ассемблерным кодом, сгенерированным компилятором^{16Чтобы облегчить чтение листинга, я пронумеровал ассемблерные инструкции}:

//
// Generated by Microsoft (R) D3DX9 Shader Compiler 9.12.589.0000
//
// Parameters:
//
// float angle;
//
//
// Registers:
//
// Name	Reg Size
// 	 	 ----
// angle	c0	1
//
//
// Default values:
//
// angle
// c0 = { 0, 0, 0, 0 };
//
vs_1_1
def c1, 0.159154937, 0.25, 0.5, -0.00138883968
def c2, 6.28318548, -3.14159274, -2.52398507e-007, 2.47609005e-005
def c3, 0.0416666418, -0.5, 1, 0 dclposition v0 dclcolor v1
add r0.w, v0.y, c0.x
mad r1.xy, r0.w, c1.x, c1.yzzw
frc r0.xy, r1
mad r0.xy, r0, c2.x, c2.y
mul r0.xy, r0, r0
mad r1.xy, r0, c2.z, c2.w
mad r1.xy, r0, r1, c1.w
mad r1.xy, r0, r1, c3.x
mad r1.xy, r0, r1, c3.y
mad r0.xy, r0, r1, c3.z
mul oPos.xy, r0, v0.x
mov oPos.zw, c3.xywz
mov oD0, v1
// approximately 15 instruction slots used

И что же мы видим? Параметру angle отведен входной регистр c0, но вот регистры c1, c2 и c3 почему-то содержат множество непонятных констант, а компактный код вершинного шейдера превратился в 13 ассемблерных инструкций, которые в действительности транслируются в 15 команд виртуального вершинного процессора. Несовпадение числа инструкций и команд обусловлено макро-инструкцией frc, разворачиваемой в три команды вершинного процессора. Окинуть одним взглядом структуру данной программы весьма проблематично, поэтому нам придется последовательно проследить выполнение программы по шагам, и попытаться понять, что же они выполняет каждая ее команда.

Примечание

Данный пример наглядно демонтирует, что короткий код вершинного шейдера вовсе не означает малый размер ассемблерной программы, и что ограничение максимальной длины программы Vertex Shader 1.1 в 128 инструкций не так уж и много.

Смысл первой команды весьма очевиден - она вычисляет сумму a = input.pos.y + angle и заносит результат в компонент w временного регистра r0. Следующая команда умножает и складывает полученное значение переменной с "чудными " константами, но ее смысл нам пока не ясен. Логично предположить, что эти действия имеют какое-то отношение к вычислению значения тригометрических функций sin и cos (виртуальный процессор Vertex Shader 1.1 не имеет инструкций для расчета синуса и косинуса). Что ж, давайте просто запишем это выражение как есть, заменив компоненты константных регистров их численными значениями:

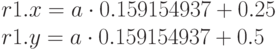
$r1.x = a \cdot 0.159154937 + 0.25\\ r1.y = a \cdot 0.159154937 + 0.5$

Присмотревшись внимательно к константе 0.159154937 мы обнаружим, что это есть нечто иное, как единица деленная на удвоенное число "пи":

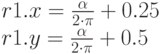
$r1.x=\frac{\alpha}{2\cdot \pi}+0.25\\ r1.y=\frac{\alpha}{2\cdot \pi}+0.5$

Следующая команда вычисляет дробную часть выражения и заносит ее в регистр r0:

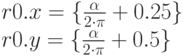
$r0.x=\{\frac{\alpha}{2\cdot \pi}+0.25\}\\ r0.y=\{\frac{\alpha}{2\cdot \pi}+0.5\}$

После обработки четвертой команды содержимое регистра r0 преобразится следующим образом:

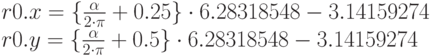
$r0.x=\{\frac{\alpha}{2\cdot \pi}+0.25\}\cdot 6.28318548 - 3.14159274\\ r0.y=\{\frac{\alpha}{2\cdot \pi}+0.5\}\cdot 6.28318548 - 3.14159274$

Нетрудно догадаться, что 3.14159274 - это число "пи", а 6.28318548 - число "пи" умноженное на два:

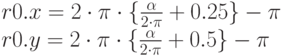
$r0.x=2\cdot \pi\cdot \{\frac{\alpha}{2\cdot \pi}+0.25\}-\pi\\ r0.y=2\cdot \pi\cdot \{\frac{\alpha}{2\cdot \pi}+0.5\}-\pi$

На первый взгляд эти формулы могут показаться сущей несуразицей, но поэкспериментировав со значениями r0.y в MathCad можно обнаружить, что они обладает двумя важными свойствами ^{17Они достаточно легко доказываются математически}:

каким бы не было значение a, r0. y всегда находится в диапазоне $[-\pi, +\pi)$
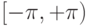
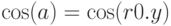
$\cos(a) = \cos(r0.y)$

Следовательно, после выполнения второй, третьей и четвертой команд угол a преобразуется к диапазону 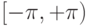$[-\pi, +\pi)$ , при этом косинус угла остается неизменным. Зачем это надо? Логично предположить, что значение косинуса будет вычисляться путем разложения в ряд Тейлора, точность которого стремительно падает с ростом модуля аргумента. Так что данное преобразование позволяет значительно повысить точность вычисления функции cos(a) для больших аргументов. Кстати, если бы не это преобразование, то по мере вращения круга точность вычислений косинуса стремительно снижалась и, в конце концов, круг перестал бы корректно вращаться.

C компонентом x регистра r0 все несколько запутаннее:

Значение r0.x находится в диапазоне $[-\pi, +\pi)$
$\sin(a) = \cos(r0.x)$

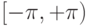
Очевидно, команды 2-4 используют известное тригонометрическое тождество 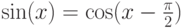$\sin(x) = \cos(x-\frac{\pi}{2})$ . Не заглядывая вперед трудно наверняка сказать, зачем компилятор HLSL выполняет данное преобразования, но с большой долей вероятности можно предположить, что синус будет вычисляться через косинус.

Что ж, давайте введем условные обозначения для углов, преобразованных к диапазону, 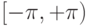$[-\pi, +\pi)$ и продолжим анализ кода:

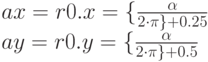
$ax=r0.x=\{\frac{\alpha}{2\cdot \pi\}+0.25}\\ ay=r0.y=\{\frac{\alpha}{2\cdot \pi\}+0.5}$

Пятая команда возводит регистр r0 в квадрат, а шестая умножает и складывает его с константами и заносит результат в регистр r1 :

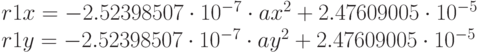
$r1x=-2.52398507\cdot 10^{-7}\cdot ax^2+2.47609005\cdot 10^{-5}\\ r1y=-2.52398507\cdot 10^{-7}\cdot ay^2+2.47609005\cdot 10^{-5}$

Шестая команда умножает регистр r1 на ax^2 и складывает с константой -0.00138883968:

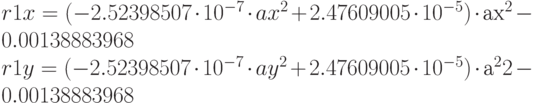
$r1x=(-2.52398507\cdot 10^{-7}\cdot ax^2+2.47609005\cdot 10^{-5})\cdot ах^2 - 0.00138883968\\ r1y=(-2.52398507\cdot 10^{-7}\cdot ay^2+2.47609005\cdot 10^{-5})\cdot а^22 - 0.00138883968$

Следующие три команды продолжают выполнение серии последовательных умножений на ax^2 и сложений с константами. В результате после выполнения десятой команды в регистре r0 оказывается следующие значение ^{18Чтобы сделать выражение удобочитаемым, число знаков в коэффициентах было уменьшено.}:

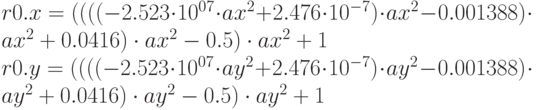
$r0.x=((((-2.523\cdot 10^{07}\cdot ax^2+2.476\cdot 10^{-7})\cdot ax^2-0.001388)\cdot ax^2+0.0416)\cdot ax^2-0.5)\cdot ax^2+1\\ r0.y=((((-2.523\cdot 10^{07}\cdot ay^2+2.476\cdot 10^{-7})\cdot ay^2-0.001388)\cdot ay^2+0.0416)\cdot ay^2-0.5)\cdot ay^2+1$

Чтобы понять смысл данного выражения раскроем скобки и упорядочим коэффициенты ax и ay по убыванию степени:

$r0.x=1-0.5\cdot ax^2+0.0416\cdot ax^4-0.001388\cdot ax^6+2.476\cdot 10^{-5}\cdot ax^8-2.523\cdot 10^{-7}\cdot ax^{10}\\ r0.y=1-0.5\cdot ay^2+0.0416\cdot ay^4-0.001388\cdot ay^6+2.476\cdot 10^{-5}\cdot ay^8-2.523\cdot 10^{-7}\cdot ay^{10}$

Дальше >>

Авторизоваться

Введение в XNA

Вершинные шейдеры

Вопросы и ответы