|
Reference = add reference, в висуал студия 2010 не могу найти в вкладке Solution Explorer, Microsoft.Xna.Framework. Его нету. |
Вершинные шейдеры
Одиннадцатая инструкция возводит input.pos.x в квадрат. Двенадцатая инструкция умножает input.pos.x на вычисленные значения тригометрических функций, завершая тем самым вычисления значения input.pos.xx * float2(sin(a), cos(a)). Тринадцатая команда выполняет сравнение значений -input.pos.x-input.pos.x и +input.pos.x-input.pos.x по следующему алгоритму:
if (-input.pos.x* input.pos.x < input.pos.x* input.pos.x) r0.w=1 else r0.w=0
Нетрудно догадаться, что данный код всегда заносит в r 0.w значение 1, если input.pos.x неравен 0, и 0 в противном случае. То есть, грубо говоря, оно эквивалентно r0.w = (input.pos.x!=0)
Теперь все встало на свои места: так как Vertex Shader 1.1 не содержит инструкции сравнения на равенство двух чисел, сообразительный компилятор HLSL реализовал проверку числа на равенство 0 через комбинацию инструкций mul и slt.
Дополнительная информация
Язык Vertex Shader 1.1 не содержит инструкции проверки двух чисел на равенство, так как потребность в ней возникает достаточно редко. Дело в том, что Vertex Shader 1.1 поддерживает только типы с плавающей точкой, сравнение которых является достаточно нестабильной операцией: достаточно малейшей ошибки в последнем разряде и два равных значения перестанут быть равными.
Но в нашем случае мы можем не опасаться каких-либо последствий потери точности: данная особенность типов half/float/double проявляется исключительно при использовании дробных чисел и обусловлено тем, что большинство конечных десятичных дробей при переводе в двоичную систему становятся бесконечными двоичными дробями. Так как разрядная сетка мантиссы конечна, эту дробь не удается точно представить и последующие операции над такими урезанными бесконечными дробями приводят к накоплению ошибки. Чтобы убедиться в наличии данной проблемы достаточно провести небольшой вычислительный эксперимент в консольном приложении C#:
// Код примера расположен в Examples\Ch05\Ex09 class Program .
{
static void Main(string[] args)
{
float a = 1.2f;
float b = 1.4f;
float c = 1.68f;
float mul = a * b;
float delta = c - mul;
+ (double)a);
+ (double)b);
+ (double)c);
" + (double)mul);
= " + (double)delta);
Console.WriteLine("a = "
Console.WriteLine("b = "
Console.WriteLine("c = "
Console.WriteLine("sum =
Console.WriteLine("delta Console.ReadKey();
}
}После выполнения примера на экране появится следующая информация:
a = 1,20000004768372 b = 1,39999997615814 c = 1,67999994754791 sum = 1,6800000667572 delta = -1,19209289550781E-07
Как видно, значения 1.2 и 1.4 не могут быть точно представлены в двоичной системе, в результате чего результат 1.68 - 1.2-1.4 оказался равен не нулю, а отрицательному числу -1.19-10-7 . Таким образом, с точки зрения компьютера 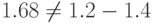 .
.
Еще раз хочу обратить ваше внимание, что данные парадоксы возникают исключительно при работе с дробными числами, которые часто (но не всегда) не могут быть точно переставлены в двоичной системе. Целые же числа всегда могут быть точно переведены в двоичное представление, поэтому работа с ними осуществляется без потери точности 22 88. В частности если мы предварительно умножим a и b на 10, то значение 12-14 окажется в точности равно 168:
a = 12 b = 14 c = 168 sum = 168 delta = 0
Примечание
Некоторые новые графические процессоры, такие как G8x , содержат инструкцию, позволяющую выполнять покомпонентное сравнение четырехмерных векторов. Соответственно, драйвера при компиляции кода шейдера в микрокод подменяет последовательность инструкций вроде mul/slt одной инструкцией сравнения.
Четырнадцатая инструкция умножает рассчитанные координаты x и y вершины на результат сравнения input.pos.x с 0: если input.pos.x!=0 , то координаты остаются без изменения, а если input.pos.x==0 , то они обнуляются. Таким образом, условное выражение
if (input.pos.x != 0)
{
...
}
else
output.pos.xy = float2(0.0, 0.0);реализуется последовательностью инструкций mul / slt / mul .
Резюмируем все вышесказанное. Компилятор HLSL успешно справился с реализацией оператора if без использования условных инструкций, но на производительности приложения это сказалось отрицательно, хотя и не фатально (на G7x время выполнения вершинного шейдера возросло на один такт).
Разумеется, при условии достаточной разрядности мантиссы.
5.5.3. Искры
После небольшого лирического отступления перейдем к моделированию полета искр средствами вершинного шейдера. Для начала освежим в памяти алгоритм генерации новых искр. Логика работы хранителя экрана выполняется с фиксированным шагом timeStep . В течение каждого дискретного шага появляется случайное количество новых искр, но не более maxScintillaCount . Каждая искра имеет случайные координаты, а так же случайную угловую и прямолинейную скорости. Время жизни каждой искры равно StartTime , по прошествии которого искра считается потухшей и ее структура может использоваться для генерации новой вершины: новые искры замещают потухшие, и лишь при отсутствии свободных потухших искр информация добавляется в конец массива вершин.
Данный алгоритм весьма проблематично реализовать в вершинном шейдере. Дело в том, что вершинный процессор обрабатывает вершины параллельно, независимо друг от друга, в результате чего вершинный шейдер не может получить информацию о состоянии других вершин. Ну а так как состояние шейдера не сохраняется между вызовами, а вернуть информацию из вершинного шейдера очень проблематично 23Для этого необходимо выполнить визуализацию во временное изображение (текстуру) и скопировать его из видеопамяти в оперативную память. Но так как данная операция является очень медленной, ее стараются использовать только в случае крайней необходимости , приложение не сможет отслеживать состояние каждой вершины и соответственно определять число потухших вершин, их индексы в массиве вершин и т.д. и т.п.
Поэтому для генерации новых вершин нам придется разработать новый алгоритм, удовлетворяющим двум требованиям:
- Постоянно изменяющиеся параметры должны быть общими для всех вершин, чтобы их можно было передавать через константные регистры.
- Обработка вершин должна идти параллельно и независимо. При этом отсутствует возможность сохранения промежуточных значений между вызовами вершинного шейдера.
Будучи зажатыми в такие жесткие рамки, мы вряд ли сможем реализовать полноценный алгоритм генерации случайных искр со случайными параметрами. Поэтому мы просто заранее рассчитаем на некотором небольшом временном интервале время появления всех искр, их координаты, скорости, цвета и т.п., после чего будем проигрывать эту последовательность "по кругу " (рисунок 5.21). Таким образом, траектория движения точек будут повторяться через некоторое время, но если длительность одной итерации будет измеряться в десятках секунд, а число искр тысячами, то пользователь вряд ли сможет заметить какую-либо цикличность в поведении искр.
Минусом данного подхода является необходимость расчета в каждом кадре всех искр массива вершин, включая потухшие искры, причем, чем сильнее продолжительность итерации превосходит время жизни вершины, тем выше будут накладные расходы. Хотя с другой стороны этот недостаток наверняка компенсируется огромной производительностью вершинного процессора 24Кроме того, в следующей главе мы примем ряд мер, призванных повысить эффективность обработки неиспользуемых вершин, в результате чего данный недостаток сведется к минимуму . Время, используемое при расчете траектории движения вершины, будет вычисляться кодом следующего вида:
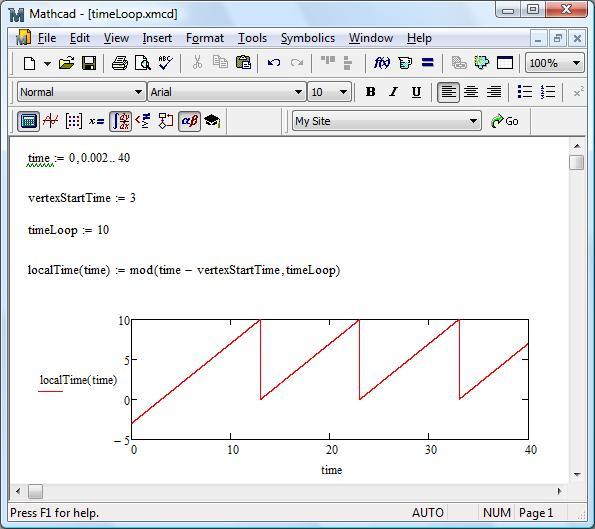
currentTime = time - vertexStartTime; localTime = currentTime % timeLoop;
где
- time - время, прошедшее с момента запуска приложения.
- vertexStartTime - время появления вершины, отсчитываемое он начала итерации. После запуска хранителя экрана идет первая итерация, то есть время отсчитывается от нуля.
- % - операция нахождения остатка от деления.
- timeLoop - длительность итерации, то есть время, через которое полет вершины повторяется заново.
- localTime - локальное время искры внутри итерации.
На рисунке 5.22 приведен график зависимости currentTime от time , построенный в Mathcad . Как видно, при запуске приложения время может быть равно отрицательному значению - это означает, что искра еще не появилась на экране. Далее по мере увеличения time локальное время так же линейно возрастает, пока не достигнет значения timeLoop , после чего оно сбрасывается до нуля и все повторяется сначала.
Разобравшись с организацией массива вершин, займемся непосредственно моделированием полета искр. Как вы помните, в хранителе экрана из четвертой главы траектория движения искры складывается как композиция движения искры из центра диска по прямой с постепенным замедлением и движения по окружности вокруг диска с постоянно уменьшающейся угловой скоростью. Собственно расчет траектории выполнялся "в лоб " путем грубой аппроксимации с малым шагом времени delta :
// Корректируем скорость прямолинейного движения. При этом вершина не должна начинать // двигаться в противоположном направлении tSpeed = Math.Max(tSpeed - tSlowing * delta, 0.0f); // Корректируем скорость вращательного движения rSpeed = Math.Max(rSpeed - rSlowing * delta, 0.0f); // Изменяем расстояние искры от центра диска distance += Speed * delta; // Изменяем угол поворота искры вокруг диска angle += Speed * delta;
Так как этот алгоритм использует рекуррентные выражения, ссылающиеся на результаты предыдущих расчетов, он не может быть использован в вершинном шейдере – для этого потребуется сохранять результаты работы вершинного шейдера между визуализацией кадров, что весьма проблематично. Поэтому нам необходимо избавиться от реккурентности. В качестве основы возьмем выражение

где
-
 - скорость вершины;
- скорость вершины; -
 - начальная скорость вершины;
- начальная скорость вершины; -
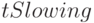 - замедление вершины;
- замедление вершины; -
 - локальное время вершины ( localtime ).
- локальное время вершины ( localtime ).
Расстояние, пройденное вершиной, может быть найдено посредством суммирования значений  , где
, где 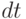 - интервал времени, стремящийся к нулю. А это есть не что иное, как интеграл
- интервал времени, стремящийся к нулю. А это есть не что иное, как интеграл  где C - константа.
где C - константа.
Значение этой константы можно легко определить из соображений, что при t=0 расстояние должно быть равно начальному положению точки  :
:

Таким образом, константа C равна начальному положению точки и в результате мы получаем окончательную формулу:
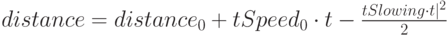 |
( 5.6) |
Но это еще не все - выражение 5.6 построено на предположение, что по достижению скоростью искры значения 0 она начинает двигаться в противоположную сторону с возрастающей скоростью, в то время как наши искры по достижению нулевой скорости должны останавливаться на месте. Для учета данного обстоятельства мы должны ограничить значение времени величиной, при котором скорость становится равна 0:
 |
( 5.7) |
где
- td - локальное время искры, которое не может превышать значение, при котором скорость объекта становится отрицательной.
Выражение для вычисления угла поворота вершины отличается от выражения расчета расстояния вершины от центра диска лишь несколькими нюансами, поэтому я сразу приведу готовый результат:
 |
( 5.8) |
где
-
 - локальное время вершины;
- локальное время вершины; -
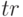 - локальное время с учетом остановки вершины по достижению скоростью нулевого значения;
- локальное время с учетом остановки вершины по достижению скоростью нулевого значения; -
 - угол поворота искры вокруг диска;
- угол поворота искры вокруг диска; -
 - скорость вращения диска;
- скорость вращения диска; -
 - текущее время;
- текущее время; -
 - локальный угол поворота вершины вокруг диска (без учета вращения самого диска);
- локальный угол поворота вершины вокруг диска (без учета вращения самого диска); -
 - начальная уголовная скорость вершины (она меньше скорости диска);
- начальная уголовная скорость вершины (она меньше скорости диска); -
 - замедление вершины.
- замедление вершины.