|
Reference = add reference, в висуал студия 2010 не могу найти в вкладке Solution Explorer, Microsoft.Xna.Framework. Его нету. |
Вершинные шейдеры
Вот уже на протяжении трех лекций мы активно используем в приложениях вершинные и пиксельные шейдеры, однако их роль сводится к банальному пропусканию через себя исходных данных без какой-либо обработки или модификации. Такой подход трудно назвать оптимальным, ведь главное предназначение шейдеров – разгрузка центрального процессора компьютера путем освобождения его от рутины. Но для этого необходимо более детально изучить язык HLSL и получить представление об архитектуре графического процессора и языках ассемблера. В виду обширности этой темы данная лекция посвящена преимущественно программированию вершинных процессоров.
Примечание
Если вы немного подзабыли основы языка HLSL, можете еще раз пролистать раздел 2.3.
5.1. Математические вычисления в HLSL
Функциональность любого шейдера так или иначе связана с математическими расчетами, поэтому для начала мы научимся выполнять математические операции над типами языка HLSL.
5.1.1. Математические операторы
Математические операторы языка HLSL частично повторяют операторы языка C. Поддерживаются операторы +, -, *, /, %, ++, --, +=, -=, *=, /= и %=. Эти операторы можно применять как над скалярными типами, так и над векторами. Операции над скалярными типами полностью аналогичны операциям языка C. Во втором случае операции осуществляется покомпонентно над элементами векторов:
float4 a = {1, 2, 3, 4};
float4 b = {5, 6, 7, 8};
// Складываем два вектора. Результат равен {1+5, 2+6, 3+7, 4+8} =
{6, 8, 10, 12}
float4 c = a+b;
// Умножаем два вектора. Вектор d станет равен {1*5, 2*6, 3*7, 4*8} =
{5, 12, 21, 32}
float4 d = a*b;Если в выражении одновременно используются скалярный и векторный тип, то операция выполняется над скалярным типом и каждым компонентом вектора:
float4 a = {1, 2, 3, 4};
// Вектор b станет равен {1*2, 2*2, 3*2, 4*2} = {2, 4, 6, 8}
float4 b = a*2;Независимо от используемых типов вычисления всегда выполняются 32-битной точностью для каждого компонента1Это утверждение верно только для вершинных шейдеров. В пиксельных шейдерах точность вычислений зависит от множества факторов (см. раздел 7.x).. Таким образом, замена в вышеприведенном коде типов float4 на half4 или double4 некоим образом не скажется на скорости или точности расчетов2А вот использование целочисленных типов вроде int4 может привести к тому, что компилятор HLSL будет пытаться честно эмулировать целочисленные вычисления посредством 32-х битных типов с плавающей точкой (см. раздел 2.3.2)..
5.1.2. Работа с компонентами векторов
DirectX предоставляет множество способов доступа к компонентам вектора. Во-первых, программист может работать с компонентами вектора как с элементами массива. В этом случае компоненты номеруются с нуля, а доступ к ним осуществляется с использованием оператора []. Например, для вычисления среднего арифметического всех компонентов вектора можно воспользоваться следующим выражением:
float4 color = float4(0.2, 0.7, 0.5, 1.0); // avg будет присвоено значение 0.6 float avg = (color[0] + color[1] + color[2] + color[3])/4;
Так как векторы очень часто используются для хранения геометрических координат и информации о цвете, DirectX предоставляет программисту возможность обращаться к компонентам вектора как к полям структуры. К нулевому элементу вектора можно обращаться как полю x или r, первому – y или g, второму – z или b, третьему – w или a. Нетрудно догадаться, что идентификаторы x, y, z, w предназначены для работы с геометрическими координатами, а идентификаторы r, g, b, a – для работы с цветовыми каналами:
float avg = (color.r + color.g + color.b + color.a)/4;
или
float avg = (color.x + color.y + color.z + color.w)/4;
При выполнении операций над векторами часто возникает необходимость выделить из вектора некоторый подвектор или переставить компоненты вектора местами. Так как современные графические ускорители поддерживают подобные операции аппаратно, разработчики HLSL встроили непосредственно в сам язык возможность гибкой работы с компонентами вектора. Например, для создания нового вектора путем комбинации компонентов существующего вектора достаточно просто перечислить после оператора ". " (точка) необходимые компоненты:
// Создаем четырехмерный вектор
float4 a={1, 2, 3, 4};
// Присваиваем двухмерному вектору b нулевой и первый элементы
вектора a. Результирующее
// значение вектора b будет равно (1, 2)
float2 b=a.xy;
// Присваиваем вектору c значение {1, 1, 2}
float3 c=a.xxy;
// Переставляем координаты x, y, z местами. Результирующее
значение вектора a будет равно
// {3, 2, 1, 4}
a.xyz=a.zyx;Примечание
Приложение должно трактовать компоненты вектора либо как цветовые каналы, либо как геометрические координаты. Комбинирование в одном выражении различных типов наименований запрещено. В частности, компилятор HLSL откажется компилировать выражение вроде a.rgzw, так как первые два компонента вектора трактуются как цвет, а вторые два – как координаты.
Другая любопытная особенность языка HLSL заключается в том, что скалярные типы фактически являются одномерными векторами. Это позволяет обращаться к скалярному типу как к массиву или структуре.
Например, код
float a=3; float4 v=float4(a, a, a, a);
можно переписать следующим образом:
float a=3; // Обращаемся к скалярному типу как к одномерному вектору float4 v=a.xxxx;
Присвоение всем компонентам вектора одного и того же значения является довольно распространенной операцией. Поэтому в HLSL предусмотрен специальный синтаксис для выполнения этой операции: при присвоении вектору скалярного выражения с использованием оператора = оно автоматически заносится во все компоненты вектора. Например:
float a=3; // В вектор v будет занесено значение (3, 3, 3, 3) float4 v=a;
5.1.3. Математические функции
В языке HLSL имеется множество математических функций для работы со скалярными и векторными типами: тригонометрические и гиперболические функции, вычисление скалярного и векторного произведения векторов и так далее. Полный список функций языка HLSL можно найти в приложении 4. Обратите внимание, что список доступных функций определяется используемым профилем.
Большинство функций HLSL транслируются в одну команду графического процессора. При этом, каждая команда графического процессора, как правило, выполняется за 1 такт. Поэтому рекомендуется как можно активнее использовать встроенные функции, а не изобретать велосипед. Например, выражение  можно записать как b=1.0/sqrt(a), либо как b=rsqrt(a). Первый вариант будет транслирован в две команды GPU (вычисление квадратного корня и деление), а второй - в одну. Нетрудно догадаться, что какой из них будет работать быстрее.
можно записать как b=1.0/sqrt(a), либо как b=rsqrt(a). Первый вариант будет транслирован в две команды GPU (вычисление квадратного корня и деление), а второй - в одну. Нетрудно догадаться, что какой из них будет работать быстрее.
Примечание
Оптимизирующий компилятор HLSL, скорее всего, самостоятельно заменит выражение b=1.0/sqrt(a) на b=rsqrt(a). Однако в более сложных случаях у него может не хватить сообразительности, чтобы подобрать оптимальную замену.
5.1.4. Черно-белая закраска
В качестве демонстрации практического использования математических расчетов мы напишем простой эффект, преобразующий цвет примитивов в черно-белый с использованием следующего выражения:
 |
( 5.1) |
где
-
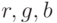 - красный, зеленый и синий цветовые каналы
- красный, зеленый и синий цветовые каналы -
 - яркость
- яркость
Это преобразование можно вставить в вершинный или пиксельный шейдер. В первом случае, цвета вершин вначале будут преобразованы в черно-белый цвет, после чего полученные черно-белые значения будут интерполироваться вдоль поверхности примитива. Следовательно, при визуализации нашего квадрата с помощью примитивов PrimitiveType.TriangleStrip преобразование в черно-белый цвет будет выполнено четыре раза - по одному для каждой вершины.
При вынесении расчетов по формуле 5.1 в пиксельный шейдер, преобразование в черно-белый цвет будет выполняться уже при вычислении цвета каждого пикселя. Например, когда визуализируемый объект занимает 56% площади окна размером 640x480, преобразование в черно-белый цвет будет осуществляться 640·480·0.56=172032 раза. То есть, по сравнению с первым вариантом объем вычислений возрастет в 172000/4=43000 раз (!), что не может не сказаться на производительности приложения. При увеличении размера окна до 1280x960 эта цифра возрастет еще в четыре раза.
Таким образом, мы можем сформулировать одно простое правило - при написании эффекта необходимо стремиться вынести как можно больше операций из пиксельного в вершинный шейдер. Поэтому в нашем эффекте мы разместим преобразование в черно-белый цвет именно в вершинном шейдере (листинг 5.1).
struct VertexInput
{
float3 pos : POSITION;
float4 color : COLOR;
};
struct VertexOutput
{
float4 pos : POSITION;
float4 color : COLOR;
};
VertexOutput MainVS(VertexInput input)
{
VertexOutput output;
output.pos = float4(input.pos, 1.0f);
// Выполняем преобразование цвета вершины в черно-белый
float luminance = (input.color.r+input.color.g+input.color.b)/3.0;
output.color.r = luminance;
output.color.g = luminance;
output.color.b = luminance; output.color.a
= input.color.a;
return output; }
float4 MainPS(float4 color:COLOR):COLOR
{
return color;
}
technique BlackAndWhiteFill
{
pass p0
{
VertexShader = compile vs_1_1 MainVS();
PixelShader = compile ps_1_1 MainPS();
}
}
Листинг
5.1.
Наш первый вариант вершинного шейдера реализует выражение 5.1 в лоб без учета архитектурных особенностей современных графических процессоров и, соответственно, не является оптимальным. Например, ничто не мешает нам присвоить рассчитанное значение яркости сразу трем цветовым компонентам (листинг 5.2).
VertexOutput MainVS(VertexInput input)
{
VertexOutput output;
output.pos = float4(input.pos, 1.0f);
// Вычисляем яркость цвета и присваиваем ее красному,
зеленому и синему каналам output.color.rgb =
(input.color.r+input.color.g+input.color.b)/3.0; output.color.a =
input.color.a;
return output;
}
Листинг
5.2.
Примечание
Вполне вероятно, что оптимизирующий компилятор HLSL самостоятельно заменит в вершинном шейдере из листинга 5.1 три присваивания компонентам вектора 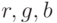 на одну векторную операцию. А может и не заменит... Поэтому имеет смысл выработать привычку активного применять векторные выражения, не особо полагаясь на сообразительность оптимизирующего компилятора.
на одну векторную операцию. А может и не заменит... Поэтому имеет смысл выработать привычку активного применять векторные выражения, не особо полагаясь на сообразительность оптимизирующего компилятора.
После этих улучшений код нашего вершинного шейдера выглядит довольно оптимально. Однако его все равно можно еще немного улучшить. Давайте раскроем скобки в выражении (5.1):
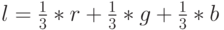 |
( 5.2) |
Если внимательно на него посмотреть, можно заметить, что оно является результатом скалярного произведения двух трехмерных векторов:
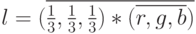 |
( 5.3) |
На первый взгляд выражение 5.3 кажется значительно более громоздким и вычислительно сложным по сравнению с выражением 5.1. Но это вовсе не так - любой современный графический процессор умеет аппаратно вычислять скалярное произведение векторов. Поэтому, если мы заменим выражение 5.1 на 5.3 и воспользуемся встроенной функцией dot (скалярное произведение), то производительность программы ощутимо возрастет (листинг 5.3).
VertexOutput MainVS(VertexInput input)
{
VertexOutput output;
output.pos = float4(input.pos, 1.0f);
// Вычисляем скалярное произведение векторов.
Второй параметрфункции dot автоматически
// преобразуется в трехмерный вектор (1/3.0, 1/3.0, 1/3.0)
output.color.rgb = dot(input.color.rgb, 1/3.0);
output.color.a = 1.0;
return output;
}
Листинг
5.3.
Использование эффекта
Чтобы опробовать полученный эффект в полевых условиях мы напишем приложение, визуализирующее квадрат с разноцветными вершинами в черно-белом режиме (рисунок 5.1). Так как код приложения не содержит ничего выдающегося, я лишь приведу фрагмент обработчика события Load (листинг 5.4), а остальные подробности при необходимости вы легко сможете найти в ![]() example.zip в каталоге Examples\Ch05\Ex01.
example.zip в каталоге Examples\Ch05\Ex01.
public partial class MainForm : Form
{
// Файл эффекта, имитирующего черно-белую закраску
const string effectFileName = "Data\\BlackAndWhiteFill.fx";
GraphicsDevice device = null; PresentationParameters
presentParams; VertexDeclaration decl = null;
// Массив вершин
VertexPositionColor[] vertices = null; Effect effect =
null;
bool closing = false;
public MainForm()
{
InitializeComponent();
}
private void MainFormLoad(object sender, EventArgs e)
{
// Создаем графическое устройство
decl = new VertexDeclaration(device, VertexPositionColor.
VertexElements);
vertices = new VertexPositionColor[4];
// Заносим в массив вершин информацию о вершинах.
Обратите внимание, что цвет вершин не
// является черно-белым
vertices[0] = new VertexPositionColor(new Vector3(-0.75f, -0.75f, 0.0f),
XnaGraphics.Color.Green);
vertices[1] = new VertexPositionColor(new Vector3(-0.75f, 0.75f, 0.0f),
XnaGraphics.Color.YellowGreen);
vertices[2] = new VertexPositionColor(new Vector3(0.75f, -0.75f, 0.0f),
XnaGraphics.Color.White);
vertices[3] = new VertexPositionColor(new Vector3(0.75f, 0.75f, 0.0f)
XnaGraphics.Color.GreenYellow);
// Загружаем и компилируем эффект
}
// Обработчики событий Paint, Resize, Closed и т.п.
}
Листинг
5.4.
Практическое упражнение №5.1
Формула (5.1) предполагает, что человеческий глаз имеет одинаковую чувствительность к красному, зеленому и синему цвету. В действительности это не так - например, человеческий глаз значительно более чувствителен к зеленому цвету, чем к синему. Для учета этого факта национальным комитетом по телевизионным системам США ( NTSC ) было принято решение вычислять яркость по следующей формуле:
 |
( 5.4) |
Создайте эффект, осуществляющий преобразование в черно-белый цвет с использованием формулы 5.4. В качестве отправной точки можно воспользоваться примером Ch05\Ex01. Готовое приложение находится в ![]() example.zip в каталоге Examples\Ch05\Ex02.
example.zip в каталоге Examples\Ch05\Ex02.
5.2. NVIDIA FX Composer 2.0
До сих пор мы создавали файлы эффектов .fx в обыкновенном текстовом редакторе. В принципе, в этом нет ничего плохого. В конце концов, некоторые разработчики создают .NET приложения в простых текстовых редакторах с последующей компиляцией полученного .cs -файла из командой строки компилятором C# ( csc.exe ). Однако по мере усложнения разрабатываемых проектов использование специализированных средств разработки становится все более актуальным. Как ни крути, та же IDE Visual Studio значительно облегчает процесс разработки благодаря умному редактору с подсветкой синтаксиса, технологии IntelliSense, интегрированному компилятору, отладчику и справочной системе.
По мере изучения XNA наши эффекты будут становиться все сложнее, поэтому будет разумно заблаговременно подыскать интегрированную среду разработки эффектов. В действительности, наш выбор не велик - на рынке сейчас господствуют два бесплатных пакета для разработки эффектов: ATI RenderMonkey 1.6 и NVIDIA FX Composer 2.0. В данном курсе мы будем использовать NVIDIA FX Composer, так как он гораздо динамичнее развивается и очень хорошо интегрирован с инфраструктурой .NET Framework.
Примечание
Существенная часть NVIDIA FX Composer 2.0 написана на .NET. В частности, вы можете легко исследовать исходный код FX Composer 2.0 посредством .NET Reflector.
Что такое FX Composer 2.0? Если коротко, это аналог Visual Studio для разработки шейдеров с использованием таких языков, как HLSL, GLSL3OpenGL Shading Language (GLSL) – язык программирования шейдеров, используемый в API OpenGL и Cg4Cg – язык программирования шейдеров, разработанный корпораций NVIDIA. Поддерживает как API DirectX, так и API OpenGL . Возможно, это слишком громко сказано, ведь FX Composer уступает Visual Studio 2005 практически по всем параметрам: удобству пользовательского интерфейса, технологии IntelliSense, документации и так далее. Кроме того, в текущей версии FX Composer имеется ощутимое количество багов. Впрочем, в этом нет ничего удивительного, если сравнить количество человеко-часов, затраченных на создание Visual Studio и FX Composer. Кроме того, NVIDIA FX Composer является абсолютно бесплатным, что позволяет закрыть глаза на многие недостатки - как известно, на халяву и уксус сладок.
FX Composer 2.0 в первую очередь ориентирован на работу с файлами формата COLLADA версии 1.4.1, поэтому для понимания основных принципов организации пользовательского интерфейса полезно ознакомиться с основами этого формата.
5.2.1. Формат COLLADA 1.4.1
COLLADA (COLLAborative Design Activity) - это кроссплатформенный открытый формат, используемый для обмена данными между приложениями создания цифрового контента ( DCC5Digital Content Creation (DCC) – создание цифрового контента ). Формат COLLADA основан на XML и задается XSD -схемой. Это очень универсальный формат, способный хранить множество видов контента:
- Трехмерные модели.
- Эффекты.
- Техники.
- Шейдеры.
- Материалы.
- Источники света.
- Камеры.
- Анимация.
- Физическая модель сцены.
- И т.д. и т.п.
Кроме того, формат COLLADA позволяет сторонним разработчикам добавлять новые элементы XML, расширяя возможности формата почти до бесконечности.
Рассмотрим основы формата COLLADA на примере простого файла:
<?xml version="1.0"?> <COLLADA xmlns="http://www.collada.org/2005/11/ COLLADASchema" version="1.4.1"> <libraryimages> <image id="mycolor" name="mycolor"> <initfrom>data/defaultcolor.dds</initfrom> </image> </libraryimages> <libraryeffects> <effect id="BlinnEffect" name="Blinn Effect"> <profileCG platform="PC-OGL"> <include sid="Blinn" url="Data/Blinn.cg"/> </profileCG> <profileCG platform="PS3"> <include sid="Blinn" url="Data/Blinn.cg"/> </profileCG> <profileGLSL> <include sid="Blinn" url="Data/Blinn.glsl"/> </profileGLSL> <extra type="import"> <technique profile="NVimport"> <import url="Data/Blinn.fx" compileroptions="" profile="fx"/> </technique> </extra> </effect> </libraryeffects> <librarymaterials> <material id="BlinnMaterial" name="Blinn Material"> <instanceeffect url="#BlinnEffect"> <!--Описание параметров материала--> </instanceeffect> </material> </librarymaterials> </COLLADA>

