Доходы аукционов с зависимыми ценностями
Сравнение аукционов первой и второй цены
Продолжаем наши штудии. На очереди — сравнение аукционов первой и второй цены.
Теорема 10.4. Ожидаемый доход от аукциона первой цены не превосходит ожидаемого дохода от аукциона второй цены.
Доказательство. В аукционе первой цены выплата равна в точности ставке победителя 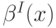 . В аукционе второй цены ожидание выплаты выигравшего агента с сигналом
. В аукционе второй цены ожидание выплаты выигравшего агента с сигналом  равно
равно
![\mathbf E\left[\vphantom{1^2}\beta^{II}(Y_1) | X_1 = x, Y_1 < x\right].](/sites/default/files/tex_cache/9a9cbff2ca44889c05e21bd36708808f.png)
Заметим, что вероятность того, что агент с сигналом  выиграет аукцион, в обоих случаях одинакова — это просто вероятность того, что сигнал
выиграет аукцион, в обоих случаях одинакова — это просто вероятность того, что сигнал  окажется наибольшим. Поэтому достаточно показать, что ожидаемая выплата в аукционе второй цены не превосходит ожидаемой выплаты в аукционе первой цены, и из этого факта сразу будет следовать утверждение теоремы.
окажется наибольшим. Поэтому достаточно показать, что ожидаемая выплата в аукционе второй цены не превосходит ожидаемой выплаты в аукционе первой цены, и из этого факта сразу будет следовать утверждение теоремы.
Вспомним, что такое 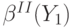 (в этом нам поможет теорема 9.1), и перепишем выражение для ожидаемой выплаты:
(в этом нам поможет теорема 9.1), и перепишем выражение для ожидаемой выплаты:
![\mathbf E\left[\beta^{II}(Y_1) | X_1 = x, Y_1 < x\right] = \\
= \mathbf E\left[\vphantom{1^2}v(Y_1,Y_1) | X_1 = x, Y_1 < x\right]
=\int_0^xv(y,y)dK(y|x),](/sites/default/files/tex_cache/9ee5e16567d013a1fa450d043647ce8b.png)
где для всех 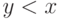
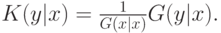
Вспомним, что  — функция распределения вероятностей на отрезке
— функция распределения вероятностей на отрезке ![[0,x]](/sites/default/files/tex_cache/47e2767cb741a37b889f1968c34f8398.png) . Кроме того,
. Кроме того,

также является функцией распределения на отрезке ![[0,x]](/sites/default/files/tex_cache/47e2767cb741a37b889f1968c34f8398.png) .
.
Далее мы покажем, что для всех 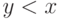
 , или, выражаясь в стиле определения 9.3,
, или, выражаясь в стиле определения 9.3,  стохастически доминирует над
стохастически доминирует над 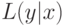 . Поскольку
. Поскольку  возрастает, из этого факта будет следовать утверждение теоремы.
возрастает, из этого факта будет следовать утверждение теоремы.
Чтобы доказать стохастическое доминирование, вспомним, что из аффилированности сигналов следует, что для всех 
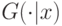 доминирует над
доминирует над  в терминах обратной доли риска. Таким образом,
в терминах обратной доли риска. Таким образом,
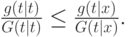
Значит, для всех 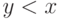
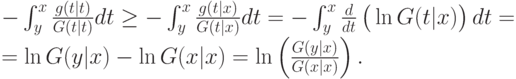
Осталось применить к обеим частям полученного равенства экспоненту, чтобы получить требуемый результат.
Пример 10.2. Вспомним предыдущий пример: пусть случайные величины 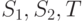 равномерны и независимы на
равномерны и независимы на ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) . Имеются два участника с сигналами
. Имеются два участника с сигналами 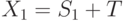 и
и 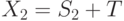 и общая ценность
и общая ценность 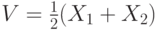 .
.
Так как участника всего два, то 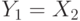 ,
,  , и, следовательно, для аукциона второй цены равновесной будет стратегия
, и, следовательно, для аукциона второй цены равновесной будет стратегия 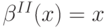 . Ожидание дохода в этом случае будет вот каким:
. Ожидание дохода в этом случае будет вот каким:
![\mathbf E\left[R^{II}\right] = \mathbf E\left[\vphantom{1^2}\min\left\{X_1,X_2\right\}\right] = \mathbf E\left[\vphantom{1^2}\min\left\{S_1,S_2\right\}\right]+\mathbf E[T] = \frac56.](/sites/default/files/tex_cache/85f882b99b43a4e8be40b5b1a0811c03.png)
В случае аукциона первой цены 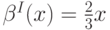 , а соответствующее ожидание дохода
, а соответствующее ожидание дохода
![\mathbf E\left[R^{I}\right] = \mathbf E\left[\max\left\{\frac23X_1,\frac23X_2\right\}\right] = \frac23\mathbf E\left[\vphantom{1^2}\min\left\{S_1,S_2\right\}\right]+\frac23\mathbf E[T] = \frac79.](/sites/default/files/tex_cache/382875252a9fdd1a7a3ddd3e2e3ce61f.png)
Таким образом, как и ожидалось, ![\mathbf E\left[R^{II}\right] > \mathbf E\left[R^I\right]](/sites/default/files/tex_cache/bacf753d4f26427e4cc02acbc7423959.png) .
.
Конец примера 10.2.
Итак, в последних двух разделах мы показали, что между математическими ожиданиями доходов английского аукциона и аукционов первой и второй цены выполняются следующие соотношения:
![\mathbf E\left[R^{\mathrm{Eng}}\right] \ge \mathbf E\left[R^{II}\right] \ge \mathbf E\left[R^I\right].](/sites/default/files/tex_cache/ae509061552223873e03b2b2d2514ba0.png)
В начале лекции мы уже упоминали, что в аукционе первой цены агенту необходимо занижать заявленную цену, чтобы избежать "проклятия победителя". Давайте для примера докажем это математически.
Теорема 10.5. В аукционе первой цены имеет место "проклятие победителя", то есть
![\beta^I(x) < \mathbf E\left[\vphantom{1^2}V_1 | X_1 = x, Y_1 < x\right].](/sites/default/files/tex_cache/0affc1aa904890ae8d401644077993a9.png)
Доказательство. Во-первых,

так как 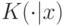 стохастически доминирует над
стохастически доминирует над 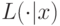 . Во-вторых,
. Во-вторых,

так как 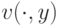 возрастает. Ну и, наконец,
возрастает. Ну и, наконец,
![\int_0^x v(x,y)dK(y | x) = \mathbf E\left[\vphantom{1^2}V_1 | X_1 = x, Y_1 < x\right].](/sites/default/files/tex_cache/e302c4067a0c071d477c230e4614aa66.png)
Теорема доказана.
Но, оказывается, "проклятие победителя" — это отнюдь не уникальное свойство аукциона первой цены.
Теорема 10.6. В аукционе второй цены "проклятие победителя" также имеет место, то есть
![\beta^{II}(x) < \mathbf E\left[\vphantom{1^2}V_1 | X_1 = x, Y_1 < x\right].](/sites/default/files/tex_cache/5bbb7be6b62af64b18dcacc559188f42.png)
Доказательство.
![\mathbf E\left[\beta^{II}(Y_1) | X_1 = x, Y_1 < x\right] = \int_0^x v(y,y)dK(y | x) \le \mathbf E\left[\vphantom{1^2}V_1 | X_1 = x, Y_1 < x\right].](/sites/default/files/tex_cache/2025c6561aeb568bf067541aa22a10b9.png)
Эффективность
Для всех трех рассмотренных выше аукционов с зависимыми ценностями найденные нами симметричные равновесные стратегии оказались возрастающими относительно неточного сигнала. Это значит, что при этих стратегиях побеждает всегда тот игрок, у которого наибольший сигнал.
Напомним, что аукцион называется эффективным, если лот всегда достается агенту, для которого он представляет наибольшую ценность. При этом не слишком важно, какой у него сигнал и является ли он наибольшим.
Поэтому неудивительно, что полученные нами симметрические равновесные стратегии могут вовсе не быть эффективными. Это покажет и следующий пример.
Пример 10.3. Рассмотрим аукцион на двоих агентов, ценности лота для которых вычисляются следующим образом:
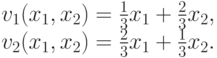
В данном случае 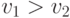 тогда и только тогда, когда
тогда и только тогда, когда 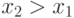 . Таким образом, у агента с более низкой ценностью сигнал будет выше, а значит, вещь достанется ему.
. Таким образом, у агента с более низкой ценностью сигнал будет выше, а значит, вещь достанется ему.
Конец примера 10.3.
Пример 10.3 достаточно сильный. Из него видно, что практически все формы аукционов могут быть неэффективными, если ценности лота для агентов зависят главным образом не от их собственной ценности, а от ценностей других агентов.
В этом разделе мы рассмотрим одно достаточное условие эффективности, которое часто выполняется в реальных ситуациях.
Определение 10.1. Будем говорить, что ценности удовлетворяют условию одного пересечения (single crossing condition), если для всех 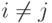 и всех
и всех 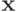 выполняется соотношение
выполняется соотношение
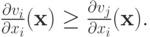
Это условие называется условием одного пересечения, потому что из него следует, что если зафиксировать сигналы всех агентов, кроме  , то
, то 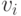 как функция от сигнала
как функция от сигнала  в каждой точке будет круче, чем
в каждой точке будет круче, чем 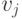 . А это, в свою очередь, означает, что они будут пересекаться не более одного раза.
. А это, в свою очередь, означает, что они будут пересекаться не более одного раза.
В случае симметричной модели с зависимыми ценностями
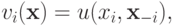
и  симметрична от последних
симметрична от последних 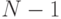 аргументов. Обозначим через
аргументов. Обозначим через 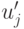 частную производную
частную производную  относительно
относительно  -го аргумента. В таком случае, чтобы проверить условие одного пересечения, достаточно убедиться, что для всех
-го аргумента. В таком случае, чтобы проверить условие одного пересечения, достаточно убедиться, что для всех 
 . Более того, поскольку
. Более того, поскольку  симметрична, достаточно лишь выполнения условия
симметрична, достаточно лишь выполнения условия  .
.
Условие одного пересечения гарантирует, что фактические (ex post) значения ценности лота для всех агентов будут упорядочены так же, как и их сигналы. А это и означает эффективность. Доказательством этого факта мы и завершим лекцию, посвященную сравнению разных типов аукционов с зависимыми ценностями.
Теорема 10.7. Пусть для симметричных зависимых ценностей и аффилированных сигналов выполняется условие одного пересечения. Тогда симметричные равновесия для аукционов первой цены, второй цены и английского аукциона являются эффективными.
Доказательство. Как мы и говорили выше, будем доказывать, что из условия одного пересечения следует то, что порядок на сигналах будет совпадать с порядком на ex post значениях ценностей. Чтобы убедиться в этом, предположим, что 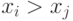 . Определим прямую, проходящую через точки
. Определим прямую, проходящую через точки 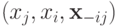 и
и 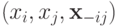 :
:
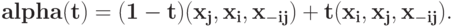
Вычислим теперь линейный интеграл по этой прямой. Как известно из математического анализа, значение (достаточно гладкой) функции в точке 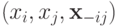 можно представить как значение функции в точке
можно представить как значение функции в точке 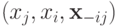 плюс интеграл от градиента этой функции по любому (достаточно гладкому) пути между этими точками (прямая замечательно подходит). Таким образом, можно записать:
плюс интеграл от градиента этой функции по любому (достаточно гладкому) пути между этими точками (прямая замечательно подходит). Таким образом, можно записать:
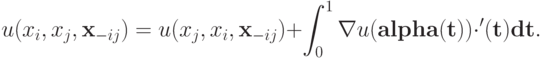
Осталось заметить, что
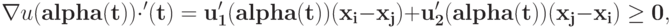
так как 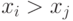 и
и  .
.
Таким образом, при 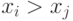 ценность для агента
ценность для агента  , которая равна
, которая равна 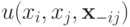 , не меньше, чем ценность для агента
, не меньше, чем ценность для агента  , равная
, равная 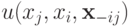 . Тем самым теорему можно считать доказанной.
. Тем самым теорему можно считать доказанной.
