Работа с графикой: визуализация функций двух переменных
7.3. Визуализация функций двух переменных на плоскости
Визуализация трёхмерных поверхностей средствами двумерной графики при помощи линий уровня подробно описывается в книге А.Н. Прокопени и А.В. Чичурина [5, с. 63–65]. Если поверхность, заданную некоторой функцией 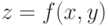 , пересечь плоскостью
, пересечь плоскостью 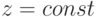 , то в сечении получится плоская кривая, которую можно спроектировать на плоскость XY. Если мы многократно осуществим такое пересечение, изменяя каждый раз значение z, и отобразим проекции всех полученных кривых на плоскость XY, то мы получим изображение пространственной поверхности в виде набора линий уровня. Подобное построение реализуется при помощи функции ContourPlot. Формат обращения к этой функции такой же, как и к иным функциям построения зависимостей двух переменных, т.е., первым аргументом указывается функция, уровни которой мы хотим построить, вторым и третьим аргументами — итераторы, определяющие переменные и интервалы их изменения.
, то в сечении получится плоская кривая, которую можно спроектировать на плоскость XY. Если мы многократно осуществим такое пересечение, изменяя каждый раз значение z, и отобразим проекции всех полученных кривых на плоскость XY, то мы получим изображение пространственной поверхности в виде набора линий уровня. Подобное построение реализуется при помощи функции ContourPlot. Формат обращения к этой функции такой же, как и к иным функциям построения зависимостей двух переменных, т.е., первым аргументом указывается функция, уровни которой мы хотим построить, вторым и третьим аргументами — итераторы, определяющие переменные и интервалы их изменения.
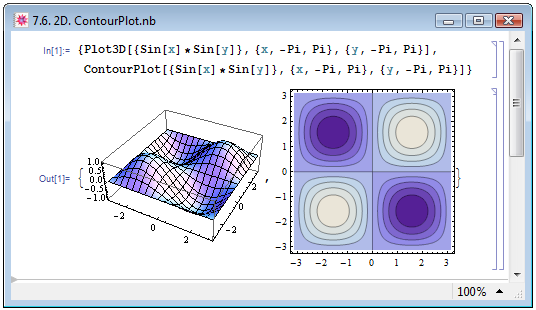
На рис. 7.6 мы для наглядности изобразили зависимость функции двух переменных ![Sin[x]*Sin[y]](/sites/default/files/tex_cache/2d5070e53089fa4569feb612d7a339dc.png) при помощи функций Plot3D (рисунок слева) и ContourPlot (рисунок справа).
при помощи функций Plot3D (рисунок слева) и ContourPlot (рисунок справа).
В качестве необязательных аргументов могут указываться дополнительные опции, меняющие внешний вид изображения.
Среди таких опций — опция Contours, которая определяет количество контурных линий на графике. Если опция задана в виде Contours->n, то количество контурных линий на рисунке будет равно n. Если опции задаётся значение в виде списка, Contours->{f1,f2,...}, то будут построены уровни, соответствующие значениям функции f1,f2,....
По умолчанию области между контурными линиями закрашиваются оттенками синего, причём области меньших значений имеют более тёмный оттенок, чем области больших значений. Самостоятельно задать стиль окрашивания можно при помощи опции ContourShading. При задании опции в виде ContourShading->None или ContourShading->False закрашивание полностью отменяется. Если мы зададим опцию в виде списка цветов c1,c2,..., т.е., ContourShading->{c1,c2,...}, то каждая область будет закрашена определённым цветом в соответствии с порядком в списке. Нумерация областей начинается с области, соответствующей наименьшему значению функции. Если в ContourShading задано n цветов, а закрашиваемых областей больше, чем n, то область с номером n+1 закрашивается цветом под номером 1 в списке, область с номером n+2 — цветом под номером 2 и т.д.
Вид контурных линий можно определять при помощи опции ContourStyle. При задании опции в виде ContourStyle->{d1,d2,...} каждая директива будет применена к области с ответствующим номером. Если количество контуров превышает количество заданных директив, то для контуров с чрезмерным номером применяется тот же принцип, что и при закрашивании областей между контурами. Если опция задана в виде ContourStyle->{{d1,d2,...}}, то все директивы d1,d2,... будут применены ко всем контурным линиям.
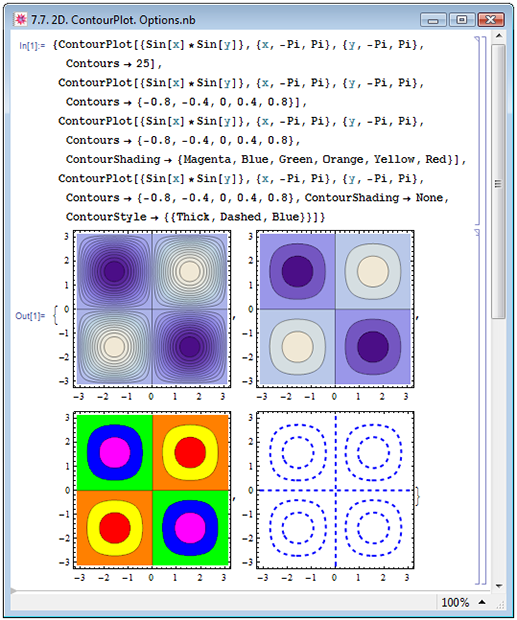
На рисунке 7.7 мы вновь построили контурное изображение функции ![Sin[x]*Sin[y]](/sites/default/files/tex_cache/2d5070e53089fa4569feb612d7a339dc.png) . Однако в первом примере (верхний левый рисунок) мы увеличили количество контурных линий, задав опцию Contours->25. Во втором примере (верхний правый рисунок) мы повлияли на выбор уровней контуров, задав Contours->{-0.8,-0.4,0,0.4,0.8}. В следующем примере (нижний левый рисунок) мы также задали способ заполнения областей между контурами, самостоятельно выбрав цвета областей, ContourShading->{Magenta,Blue,Green,Orange,Yellow,Red}. В последнем примере (нижний правый рисунок) мы вовсе отказались от закрашивания областей, ContourShading->None, зато особым образом выделили все линии контуров, сделав их толстыми, штриховыми и синего цвета, ContourStyle->{{Thick,Dashed,Blue}}.
. Однако в первом примере (верхний левый рисунок) мы увеличили количество контурных линий, задав опцию Contours->25. Во втором примере (верхний правый рисунок) мы повлияли на выбор уровней контуров, задав Contours->{-0.8,-0.4,0,0.4,0.8}. В следующем примере (нижний левый рисунок) мы также задали способ заполнения областей между контурами, самостоятельно выбрав цвета областей, ContourShading->{Magenta,Blue,Green,Orange,Yellow,Red}. В последнем примере (нижний правый рисунок) мы вовсе отказались от закрашивания областей, ContourShading->None, зато особым образом выделили все линии контуров, сделав их толстыми, штриховыми и синего цвета, ContourStyle->{{Thick,Dashed,Blue}}.
Подробней о функции построения контурных изображений и её опциях см. книги Е. М. Воробьёва [1, с. 81–82], В. П. Дьяконова [2, с. 416–419] и А. Н. Прокопени и А. В. Чичурина [5, с. 63–64].
увеличить изображение
Рис. 7.7. Изменение внешнего вида контурных графиков функций двух переменных при помощи опций
Для двумерного представления функции двух переменных используется также функция DensityPlot. Она разбивает область изменения каждого из аргументов на некоторое количество одинаковых отрезков, формируя тем самым регулярную сетку квадратных ячеек. Значение функции в каждой ячейке отображается при помощи окрашивания этой ячейки в определённый цвет. Правила окрашивания по умолчанию такие же, как и для ContourPlot: ячейка с меньшим значением функции будет иметь более тёмный цвет. Таким образом, третьей координатой, соответствующей значению функции, выступает цвет.
По умолчанию область изменения каждого аргумента разбивается на 14 отрезков, то есть, всё изображение разбивается на 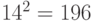 ячеек. Однако количеством отрезков можно манипулировать при помощи опции PlotPoints. Она задаёт число точек на интервале, между которыми будут формироваться отрезки. Таким образом, число отрезков всегда будет на 1 меньше, чем число точек, заданных опцией PlotPoints. Заданная в виде PlotPoints->k опция способствует разбиению области изменения каждого аргумента на k-1 отрезков. Если задать опцию в виде списка двух элементов, PlotPoints->{m,n}, то интервал вдоль оси абсцисс разбивается на m-1 отрезков, а вдоль оси ординат — на n-1 отрезков.
ячеек. Однако количеством отрезков можно манипулировать при помощи опции PlotPoints. Она задаёт число точек на интервале, между которыми будут формироваться отрезки. Таким образом, число отрезков всегда будет на 1 меньше, чем число точек, заданных опцией PlotPoints. Заданная в виде PlotPoints->k опция способствует разбиению области изменения каждого аргумента на k-1 отрезков. Если задать опцию в виде списка двух элементов, PlotPoints->{m,n}, то интервал вдоль оси абсцисс разбивается на m-1 отрезков, а вдоль оси ординат — на n-1 отрезков.
Для функции DensityPlot также может быть задана опция Mesh. Однако поскольку проекциями линий задаваемой этой опцией криволинейной сетки на отображаемую плоскость являются прямые, то опция Mesh в функции DensityPlot по сути генерирует равномерную сетку с одинаковыми прямоугольными ячейками. Число линий этой сетки определяется опцией PlotPoints. Таким образом, чтобы проверить, на какое количество ячеек было разбито плотностное изображение, следует задать опцию в виде Mesh->Full.
По умолчанию ячейки окрашиваются градациями синего. Однако способ окрашивания можно изменять при помощи опции ColorFunction. Задание опции в виде ColorFunction->GrayLevel изобразит рисунок в градациях серого: при этом наименьшему значению визуализируемой функции соответствует чёрный цвет, а наибольшему — белый. Чтобы окрасить изображение в цвета Hue-палитры, следует задать опцию как ColorFunction->Hue. Для того чтобы ячейки отличались друг от друга оттенками одного и того же цвета, следует воспользоваться уже известной нам директивой Hue[h,s,b], задав ColorFunction->(Hue[h,s,#]&), где нужно самостоятельно указать значения h и s. Кроме того, можно просто воспользоваться стандартной цветовой схемой, окрасив, например, изображения в "цвета солнца": ColorFunction->"SolarColors".
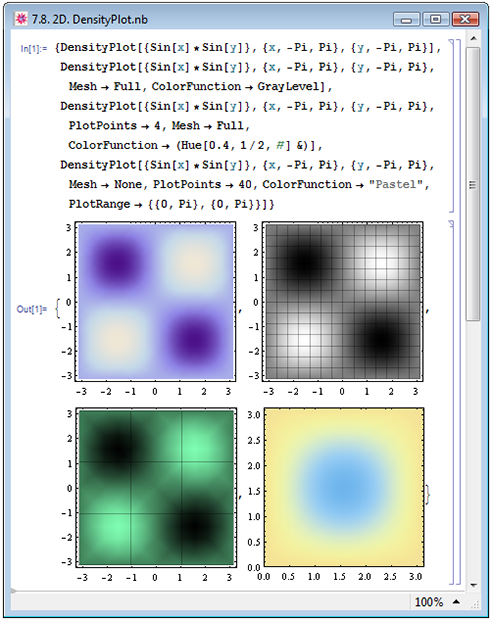
Изобразим на рисунке 7.8 прежнюю функцию ![Sin[x]*Sin[y]](/sites/default/files/tex_cache/2d5070e53089fa4569feb612d7a339dc.png) при помощи DensityPlot с разными значениями опций. В первом примере (верхний левый рисунок в Out[1]) мы обошлись без дополнительных опций. Во втором примере (верхний правый рисунок) мы накинули на график координатную сетку, Mesh->Full, чтобы убедиться, что по умолчанию область разбилась на 14x14 ячеек, а также окрасили изображение в оттенки серого, ColorFunction->GrayLevel. В следующем примере (нижний левый рисунок) мы уменьшили до трёх число отрезков вдоль каждого направления, PlotPoints->4, и теперь имеем наглядное представление того, как это влияет на качество изображения. Кроме того, мы окрасили изображение в зелёный цвет, задав в качестве изменяющейся координаты в зависимости от значения функции его яркость, ColorFunction->(Hue[0.4,1/2,#]&). В последнем примере (нижний правый рисунок) мы известным нам ранее способом нарисовали фрагмент полного изображения, PlotRange->{{0,Pi},{0,Pi}}, избавились от координатной сетки поверх изображения, Mesh->None, значительно увеличили число отрезков вдоль каждого направления, PlotPoints->40 (что положительно повлияло на качество изображения), а также окрасили рисунок в спокойные "пастельные" тона, используя соответствующую стандартную цветовую схему, ColorFunction->"Pastel".
при помощи DensityPlot с разными значениями опций. В первом примере (верхний левый рисунок в Out[1]) мы обошлись без дополнительных опций. Во втором примере (верхний правый рисунок) мы накинули на график координатную сетку, Mesh->Full, чтобы убедиться, что по умолчанию область разбилась на 14x14 ячеек, а также окрасили изображение в оттенки серого, ColorFunction->GrayLevel. В следующем примере (нижний левый рисунок) мы уменьшили до трёх число отрезков вдоль каждого направления, PlotPoints->4, и теперь имеем наглядное представление того, как это влияет на качество изображения. Кроме того, мы окрасили изображение в зелёный цвет, задав в качестве изменяющейся координаты в зависимости от значения функции его яркость, ColorFunction->(Hue[0.4,1/2,#]&). В последнем примере (нижний правый рисунок) мы известным нам ранее способом нарисовали фрагмент полного изображения, PlotRange->{{0,Pi},{0,Pi}}, избавились от координатной сетки поверх изображения, Mesh->None, значительно увеличили число отрезков вдоль каждого направления, PlotPoints->40 (что положительно повлияло на качество изображения), а также окрасили рисунок в спокойные "пастельные" тона, используя соответствующую стандартную цветовую схему, ColorFunction->"Pastel".
Подробней о функции построения плотностных изображений и её опциях см. книги Е. М. Воробьёва [1, с. 82–83], В. П. Дьяконова [2, с. 419–420] и А. Н. Прокопени и А. В. Чичурина [5, с. 64–65].
увеличить изображение
Рис. 7.8. Визуализация функции двух переменных средствами двумерной графики при помощи функции DensityPlot
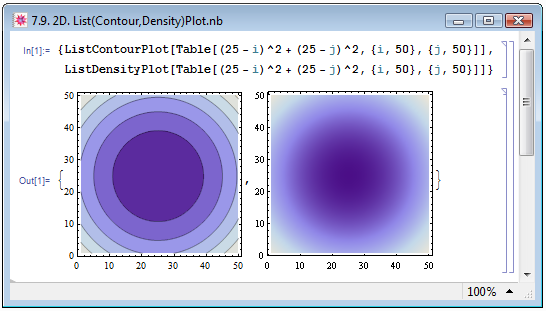
На основе уже имеющихся знаний о функциях ListPlot3D, ContourPlot и DensityPlot не составляет никакого труда разобраться в действии функций ListContourPlot и ListDensityPlot, предназначенных для двумерного представления дискретных зависимостей от двух переменных. В настоящем курсе мы лишь приведём примеры использования функций контурной визуализации (левое изображение) и плотностной визуализации (правое изображение) некоторой дискретной зависимости на рисунке 7.9. Управление характеристиками изображения дискретных зависимостей при помощи опций полностью аналогично таковому для непрерывных зависимостей.