Работа с графикой: визуализация функций двух переменных
Цель лекции: познакомиться с принципами создания в Mathematica двумерных и трёхмерных объектов и принципами работы с ними.
7.0. Введение
В предыдущей лекции мы познакомились с принципами визуализации данных, научились строить двумерные графики непрерывных и дискретных зависимостей от одной переменной. В настоящей лекции мы продолжим знакомство с графическими возможностями системы Mathematica и научимся визуализировать зависимости от двух и трёх переменных средствами двумерной и трёхмерной графики. Кроме того, мы научимся визуализировать динамические процессы, когда меняется один или несколько параметров. В качестве основы рассмотрения по-прежнему будем использовать книгу Е. М. Воробьёва [1].
7.1. Визуализация функций двух переменных в трёхмерном пространстве
Функция двух переменных определяет в трёхмерном пространстве некоторую поверхность. Встроенные функции Mathematica для работы с трёхмерной графикой, оканчиваются на Plot3D.
Для создания трёхмерных графических объектов предназначены функции Plot3D, ParametricPlot3D и ListPlot3D.
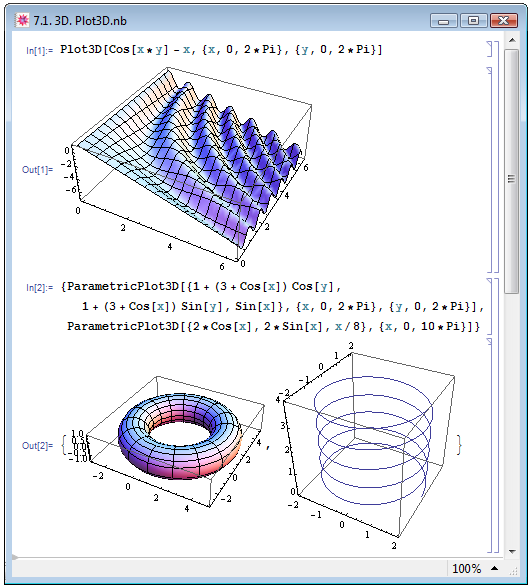
Формат обращения к функции Plot3D отличается от такового для функции Plot третьим обязательным аргументом: Plot3D[func,{x,xmin,xmax},{y,ymin,ymax}], где func — заданная функция переменных x и y, меняющихся на отрезках от xmin до xmax и от ymin до ymax, соответственно. На рисунке 7.1 в качестве примера (In[1]) мы построили поверхность, заданную функцией Cos[x*y]-x.
Функция ParametricPlot3D позволяет строить параметрически заданные зависимости: как поверхности, так и кривые в трёхмерном пространстве. В примере Out[2] на рис. 7.1 слева мы параметрически построили поверхность — тор, задав функциональную зависимость от двух переменных. В примере Out[2] справа мы изобразили в трёхмерном пространстве кривую, иллюстрирующую параметрическую зависимость от одной переменной.
Подробней о функциях Plot3D и ParametricPlot3D см. книги Е. М. Воробьёва [1, с. 83–86] и А. Н. Прокопени и А. В. Чичурина [5, с. 58–63].
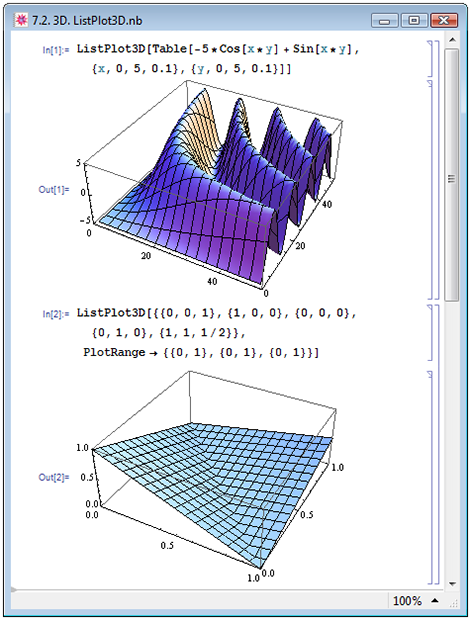
Для трёхмерного графического представления дискретных численных данных используется функция ListPlot3D. Если единственный аргумент функции задан в виде матрицы mxn, т.е., в виде {{v11,v12,...,v1n},{v21,v22,...,v2n},...,{vm1,vm2,...,vmn}}, то данные в ячейке матрицы vij рассматриваются как z-координаты (по оси аппликат) точки в трёхмерном пространстве, а координатам по осям абсцисс и ординат соответствуют значения x=i и y=j (пример In[1] на рис. 7.2). Подобный способ задания возможен, если значение n не равняется 3.
Если аргумент задан в виде матрицы, содержащей 3 столбца (т.е., матрица mxn, где n=3), то элементы матрицы интерпретируются иным образом: каждая точка i списка {{x1,y1,z1},{x2,y2,z2},...,{xm,ym,zm}} обладает координатами {xi,yi,zi} (пример In[2] на рис. 7.2).
О функции ListPlot3D см. книгу В. П. Дьяконова [2, с. 429–430].