Сервисы MATHCAD 14: реализация технологий экономико-математического моделирования
[+]
Уральский государственный экономический университет
Опубликован: 27.05.2014 | Доступ: свободный | Студентов: 471 / 50 | Длительность: 11:44:00
Темы: Математика, Экономика, Образование
Лекция 3:

Межотраслевой баланс
A
|
версия для печати
< Лекция 2 || Лекция 3: 1234 || Лекция 4 >

3.3. Нахождение матрицы прямых затрат и конечного продукта по данным межотраслевых поставок и валовой продукции

Рассмотрим другую задачу. По данным межотраслевых поставок и валовой продукции найдем структурную матрицу А и вектор конечного спроса Y.

Задача 3.2.

Рассмотрим 3 сектора экономики6 промышленность, сельское хозяйство и транспорт. Отчетный межотраслевой баланс этих отраслей: стоимости средств производства, произведенных в каждой отрасли и потребленных другими отраслями и валовая продукция приведены в таблице. (цифры условные).

Производящие отрасли промышленность Сельское хозяйство Транспорт Валовая продукция X
Потребляющие отрасли Межотраслевые Поставки
промышленность 20,00 5,00 20,00 200
Сельское хозяйство 60,00 0,00 15,00 100
Транспорт 40,00 40,00 0,00 100
Чистая продукция V

Найти

  1. Матрицу коэффициентов прямых затрат.
  2. Определить для каждой отрасли конечный объем продукции Y.
  3. Определить объемы чистой продукции
  4. Выполнить проверку проведенных вычислений, заполнить матрицу МОБ.

Уравнения:

  • Коэффициенты прямых затрат а_{ij}=x_{ij} /X_j
  • Y= (E-A) X
  • Условно чистая продукция V_j=X_j-\sum_{i=1}^{n}x_{i,j}_j ( сумма по строкам)

Проверка проведенных вычислений. В таблице МОБ рассчитываем :

  • Столбец конечный продукт V_i=X_i-\sum_{j=1}^{n}x_{ij} (сумма по столбцам)
  • Строка Валовая продукция -X_j=(X_i)^T
  • Суммарный конечный продукт равен суммарной условно чистой продукции \sum_{i=1}^{n}Y_i=\sum_{j=1}^{n}V_j

Решение. Для расчета в Mathcad используются операции с матрицами и с индексными переменными .

Входные данные

Матрица межотраслевых затрат: x:=\begin{pmatrix} 20 & 5 & 20 \\ 60 & 0 & 15 \\ 40 & 40 & 0 \end{pmatrix}

Вектор валовой продукции: X:=\begin{pmatrix} 200\\ 100\\ 100\end{pmatrix}

Решение:

ORIGIN:=1

Вводим единичную матрицу: identity(3)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

E:=identity(3)

i:=1..3, \;j=1..3

Матрица прямых затрат: A_{i,j}:=\frac{x_{i,j}}{X_j}, x:=\begin{pmatrix} 0.1& 0.05 & 0.2\\ 0.3& 0 & 0.15 \\ 0.2& 0.4 & 0 \end{pmatrix}

Вектор конечной продукции: Y:=(E-A)\cdot X, Y:=\begin{pmatrix} 155\\ 25\\ 20\end{pmatrix}

Проверка проведенных вычислений. Расчет матрицы МОБ,

Добавленная стоимость (чистая продукция): 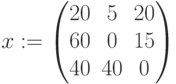x:=\begin{pmatrix} 20 & 5 & 20 \\ 60 & 0 & 15 \\ 40 & 40 & 0 \end{pmatrix}

\sum_{i=1}^{3}x_{i,j}

\begin{array}{|c|} \hline 120 \\ \hline 45 \\ \hline 35 \\ \hline \end{array}

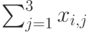
\sum_{j=1}^{3}x_{i,j}

\begin{array}{|c|} \hline 45 \\ \hline 75 \\ \hline 80 \\ \hline \end{array}

Вектор конечной продукции: V_j:=X_j-\sum_{i=1}^{3}x_{i,j}, V^T=(80\;55\;65)

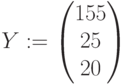
Y_j=X_i-\sum_{j=1}^{3}x_{i,j}, Y:=\begin{pmatrix} 155\\ 25\\ 20\end{pmatrix}

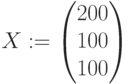
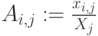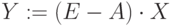\sum_{j=1}^{3}V_j=200

\sum_{j=1}^{3}Y_i=200

Дальше >>
< Лекция 2 || Лекция 3: 1234 || Лекция 4 >

Вопросы и ответы

вопросов: 0