Обслуживание полнодоступной группы потребителей от группы с ограниченным числом партий товаров (формула Энгсета)
5.4. Задачи
Задача 1
Рассмотрим маленькие сельские рынки с числом продавцов 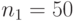 ,
, 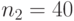 ,
, 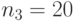 .
.
Заданы потери - доля непроданных грибов должна быть 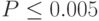 .
.
Максимальная продажа грибов одним продавцом и 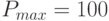 грибов в день.
грибов в день.
Определить при заданных потерях продавцов:
- Необходимое количество покупателей

- Среднюю величину покупки каждым покупателем (в относительных единицах и в числе штук.)
- Общее обслуженное рынком предложение
Решение.
По таблицам формулы Энгсета (Приложение 2).
Надо для заданной величины потерь и заданного числа продавцов определить необходимое число покупателей  .
.
Для  ,
, 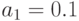 отн. ед (среднее число приобретаемое 1 покупателем 10 штук в день)
отн. ед (среднее число приобретаемое 1 покупателем 10 штук в день)
Для 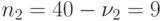 ,
, 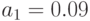 отн. ед (среднее число приобретаемое 1 покупателем 9 штук в день)
отн. ед (среднее число приобретаемое 1 покупателем 9 штук в день)
Для 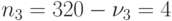 ,
, 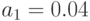 отн. ед (среднее число приобретаемое 1 покупателем 4 штуки в день)
отн. ед (среднее число приобретаемое 1 покупателем 4 штуки в день)
Сравним полученные результаты расчета характеристик на основании примитивного потока с результатами, а которых систему исследовали с помощью простейшего потока
Для этого определим величину обслуженного предложения каждым из заданных рынков.
Общее обслуженное предложение
Для 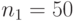
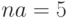 отн.ед.
отн.ед.
Для 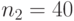
 отн. ед.
отн. ед.
Для 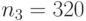
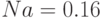 отн.ед.
отн.ед.
По таблице Эрланга Приложение 1
Определим число покупателей необходимое для обеспечения потерь 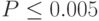 .
.
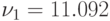

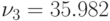
Полученные результаты показывают, что необоснованное применение модели с простейшим потоков даёт завышение числа покупателей (необходимого спрос). И тем больше, чем меньше число продавцов (чем меньше величина предложения).
Задача 2
В фирме по ремонту компьютеров работают 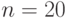 мастеров- ремонтников обслуживает
мастеров- ремонтников обслуживает 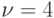 группы пользователей.
группы пользователей.
Рассмотрим три варианта величины поступления заявок от каждого пользователя
- 2.5 заявки в мес.
- 2.8 заявки в мес.
- 3 заявки в мес.
Если максимальное число заявок на обслуживание мастером от одного пользователя не может превышать в мес. 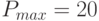 заявок в мес., то это составляет
заявок в мес., то это составляет
-
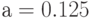 в мес.;
в мес.; -
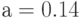 в мес.;
в мес.; -
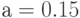 в мес.;
в мес.;
Длительность обслуживания одной заявки (длительность потребления) 1 час. Если необходимо большее время будем в расчете принимать как большее число заявок.
Определить, потери для примитивного потока
Будем рассматривать три вида потерь.
- Потери по заявкам
 , которые заключаются в том, что заявка на ремонт поступила в момент, когда заняты все n мастеров (число заявок больше
, которые заключаются в том, что заявка на ремонт поступила в момент, когда заняты все n мастеров (число заявок больше  ).
). - Потери по времени
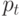 , которые заключаются в том, что в данный период времени все мастера заняты (время наибольшего потребления).
, которые заключаются в том, что в данный период времени все мастера заняты (время наибольшего потребления). - Потери по товарам
 , которые заключаются в том, что в данный период времени у мастеров нет достаточного запаса времени для облуживания данной заявки ( поступила заявка требующая 2 часа, есть свободные мастера, но ни у одного мастера нет такого запаса времени).
, которые заключаются в том, что в данный период времени у мастеров нет достаточного запаса времени для облуживания данной заявки ( поступила заявка требующая 2 часа, есть свободные мастера, но ни у одного мастера нет такого запаса времени).
Решение.
Определяем потери для примитивного потока.
По таблицам формулы Энгсета определяем значения потерь по заявкам 
 ;
; 
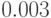
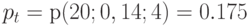 ;
; 
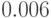
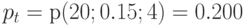 ;
; 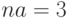
Определим потери товара 
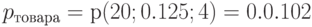
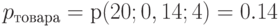
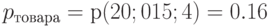 ;
;
Потери по заявкам 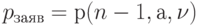 не приводятся в виду отсутствия таблиц для такого значения
не приводятся в виду отсутствия таблиц для такого значения  .
.
