|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Операторы управления
3.5.6 Ввод данных из диалогового окна в среде Lazarus
Окно ввода — это стандартное диалоговое окно, которое появляется на экране в результате вызова функции InputBox. В общем виде оператор ввода данных с использованием этой функции записывают так:
имя:= InputBox (заголовок_окна,подсказка,значение );
где
- заголовок_окна — строка, определяющая название окна;
- подсказка — текст поясняющего сообщения;
- значение — строка, которая будет находиться в поле ввода при появлении окна на экране;
- имя — переменная строкового типа, которой будет присвоено значение из поля ввода.
После выполнения фрагмента программы
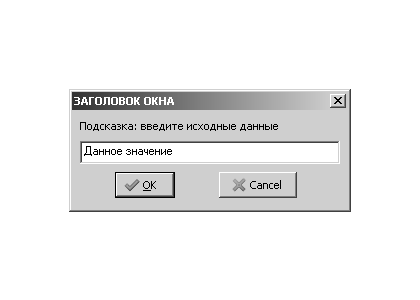
var S : string; begin S:= InputBox ( ’ЗАГОЛОВОК ОКНА ’, ’Подсказка : введите исходные данные ’, ’Данное значение ’ ); end;
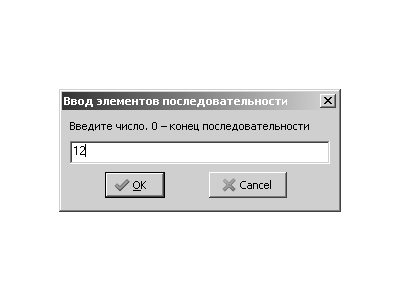
появится окно, представленное на рис. 3.37.
У пользователя есть возможность изменять текст в поле ввода. Щелчок по кнопке ОК приведёт к тому, что в переменную, указанную слева от оператора присваивания, будет занесена строка, находящаяся в поле ввода. В данном случае в переменную S будет записана строка ’Данное значение’. Щелчок по кнопке Cancel закроет окно ввода.
Учитывая, что функция InputBox возвращает строковое значение, при вводе числовых данных применяют функции преобразования типов:
var S : string; gradus, radian : real; begin S:= InputBox ( ’Ввод данных ’, ’Введите величину угла в радианах ’, ’ 0,000 ’ ); gradus := StrToFloat ( S ); radian := gradus * pi / 1 8 0; MessageDlg ( ’Величина угла в градусах ’ +FloatToStr ( radian ), MtInformation, [ mbOk ], 0 ); end;
Можно применять диалоговое окно при решении задач, обрабатывающих некоторые числовые последовательности. Рассмотрим несколько таких задач.
 вещественных чисел. Определить наибольший элемент последовательности.
вещественных чисел. Определить наибольший элемент последовательности.Входные данные: N — целое число; Х — вещественное число, определяет текущий элемент последовательности.
Выходные данные: Max — вещественное число, элемент последовательности с наибольшим значением.
Промежуточные переменные: i — параметр цикла, номер вводимого элемента последовательности.
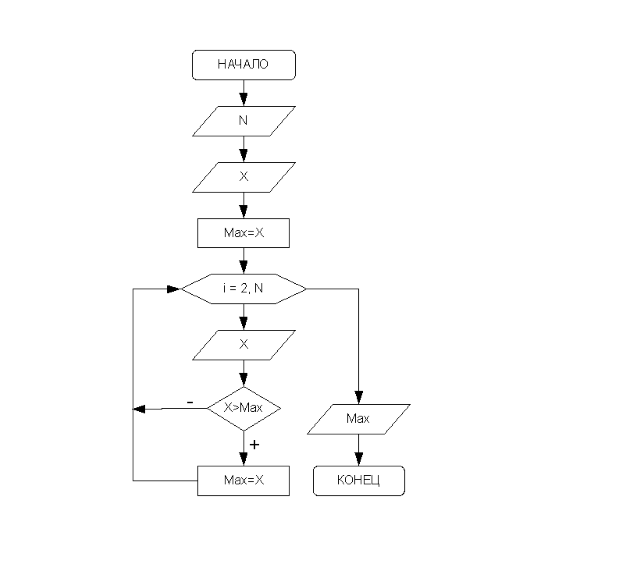
Алгоритм поиска наибольшего элемента в последовательности следующий (рис. 3.38).
В памяти компьютера отводится ячейка, например, с именем Max, в которой будет храниться наибольший элемент последовательности — максимум. Вводим количество элементов последовательности и первый элемент последовательности. Предполагаем, что первый элемент последовательности наибольший, и записываем его в Max. Затем вводится второй элемент последовательности и сравнивается с предполагаемым максимумом. Если окажется, что второй элемент больше, его записываем в ячейку Max. В противном случае никаких действий не предпринимаем. Потом переходим к вводу следующего элемента последовательности, и алгоритм повторяется с начала. В результате, в ячейке Max будет храниться элемент последовательности с наибольшим значением13Для поиска наименьшего элемента последовательности (минимума), предполагают, что первый элемент — наименьший, записывают его в ячейку Min, а затем среди элементов последовательности ищут число, значение которого будет меньше, чем предполагаемый минимум.
Разместим на форме объект типа надпись Label1 и кнопку Button1 (см. рисунок 3.39). Щелчок по кнопке приведёт к выполнению следующей процедуры:
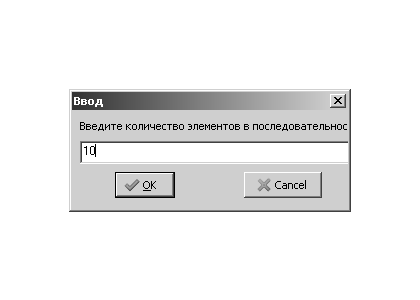
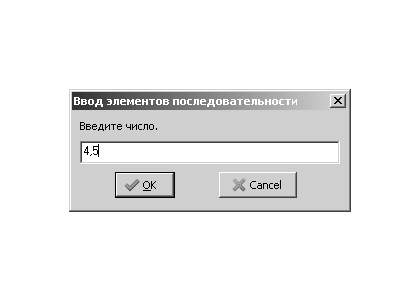
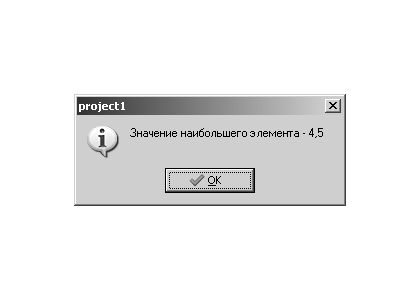
procedure TForm1. Button1Click ( Sender : TObject ); var i,N: integer; max,X: real; S : string; begin //Ввод количества элементов последовательности. S:= InputBox ( ’Ввод ’, ’Введите_количество элементов в последовательности. ’, ’ 0 ’ ); N:= StrToFloat ( S ); //Ввод первого элемента последовательности. S:= InputBox ( ’Ввод элементов последовательности ’, ’Введите число. ’, ’ 0 ’ ); X:= StrToFloat ( S ); //Предположим, что первый элемент максимальный — Max=X. max:=X; //Параметр цикла принимает стартовое значение i=2, //т.к. первый элемент уже введён. for i :=2 to N do begin //Ввод следующих элементов последовательности. S:= InputBox ( ’Ввод элементов последовательности ’, ’Введите число. ’, ’ 0 ’ ); X:= StrToInt ( S ); //Если найдётся элемент, превышающий максимум, //записать его в ячейку Max — //теперь он предполагаемый максимум. if X>max then max:=X; end; //Вывод наибольшего элемента последовательности. MessageDlg ( ’Значение наибольшего элемента - ’ +FloatToStr (max ), MtInformation, [ mbOk ], 0 ); end;
Результаты работы программы представлены на рис. 3.39,3.40,3.41,3.42.
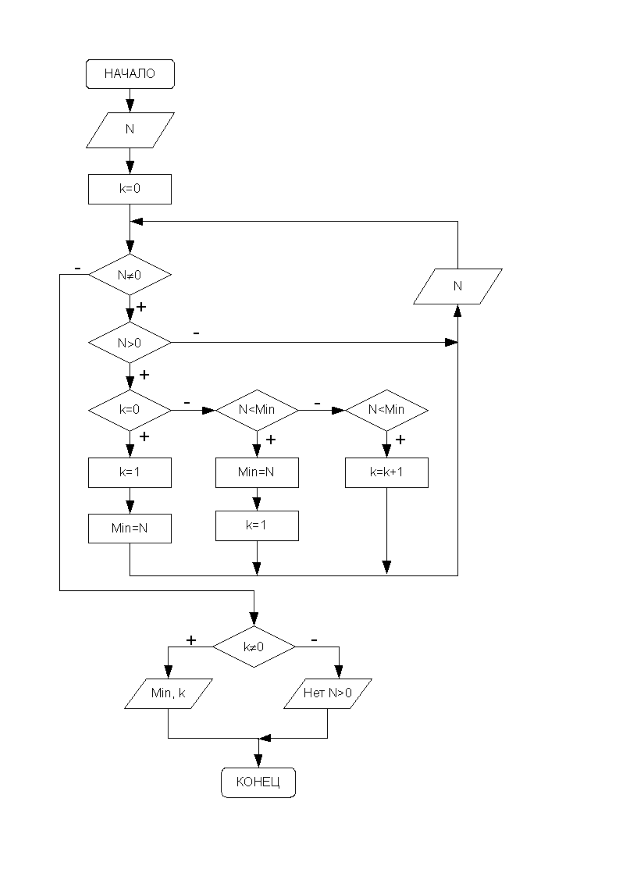
Блок-схема решения задачи приведена на рис. 3.43.
увеличить изображение
Рис. 3.43. Алгоритм поиска минимального положительного числа в последовательности
Далее приведён текст подпрограммы с подробными комментариями14Алгоритм поиска максимального (минимального) элементов последовательности подробно описан в задаче 3.18.. Подпрограмма выполняется при обращении к кнопке Button1, предварительно размещённой на форме.
procedure TForm1. Button1Click ( Sender : TObject ); var N, k, min : integer; S : string; begin //Ввод первого элемента последовательности. S:= InputBox ( ’Ввод элементов последовательности ’, ’введите_число. 0 - конец последовательности ’, ’ 0 ’ ); N:= StrToInt ( S ); //Предположим, что положительных чисел нет — K=0. В переменной //K будет храниться количество минимумов среди положительных //чисел. k : = 0; //Пока введённое число не равно нулю, выполнять тело цикла. while N<>0 do begin //Проверяем, является ли введённое число положительным. if N>0 then begin //Если N>0 и K=0, поступил 1-й положительный элемент, //предположим, что он минимальный Min=N, соответственно, //количество минимумов равно 1. if k=0 then begin k : = 1; min:=N; end //Если элемент не первый, сравниваем его //с предполагаемым минимумом; //если элемент меньше, записываем его //в Min и обнуляем счетчик. else if N<min then begin min:=N; k : = 1; end //Если элемент равен минимуму, //увеличиваем количество минимумов на 1. else if N=min then k:=k+1; end; //Ввод следующего элемента последовательности. S:= InputBox ( ’Ввод элементов последовательности ’, ’введите число. 0 - конец последовательности ’, ’ 0 ’ ); N:= StrToInt ( S ); end; //Конец цикла. if k<>0 then //Если значение счётчика не равно нулю, //выводим значение минимального элемента и //количество таких элементов, MessageDlg ( ’MIN = ’+IntToStr ( min)+ ’ K= ’+IntToStr ( k ), MtInformation, [ mbOk], 0 ) else //в противном случае сообщаем, //что положительных чисел нет. MessageDlg ( ’Положительных чисел нет ’, MtInformation, [ mbOk ], 0 ); end;
 произвольных чисел меняет знак.
произвольных чисел меняет знак.Чтобы решить задачу, нужно попарно перемножать элементы последовательности. Если результат произведения пары чисел — отрицательное число, значит, эти числа имеют разные знаки.
Пусть  — количество смен знака последовательности — равно 0.
— количество смен знака последовательности — равно 0.
Пусть в переменной А хранится текущий элемент последовательности, а в переменой В — предыдущий. Введём N — количество элементов последовательности. Организуем цикл (переменная i меняется от 1 до N). В цикле будем делать следующее: вводим очередной элемент последовательности (A); если это это первый элемент последовательности (i=1), то сравнивать его не с чем, и просто переписываем переменную A в переменную B (B:=A). Если это не первый последовательности ( ), то проверяем знак произведения
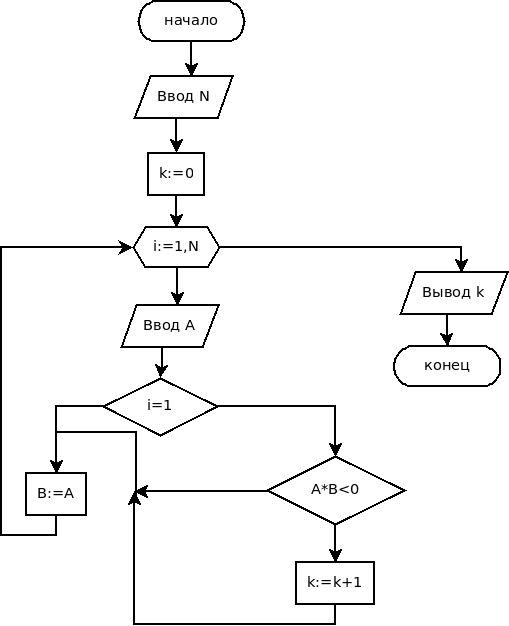
), то проверяем знак произведения  (текущего и предыдущего элемента последовательности). Если произведение отрицательно, то счётчик k увеличиваем на 1. После чего не забываем в переменную B записать A. Блок-схема алгоритма приведена на рис. 3.44.
(текущего и предыдущего элемента последовательности). Если произведение отрицательно, то счётчик k увеличиваем на 1. После чего не забываем в переменную B записать A. Блок-схема алгоритма приведена на рис. 3.44.
Разметим на форме два объекта типа надпись Label1 и Label2, объект поле ввода Edit1 и кнопку Button1 (рис. 3.45).
Текст подпрограммы, которая будет выполнена при обращении к кнопке, приведён далее.
procedure TForm1. Button1Click ( Sender : TObject ); var N, A, B, i, k : integer; S : string; begin N:= StrToInt ( Edit1. Text ); S:= InputBox ( ’Ввод элементов последовательности ’, ’Введите число. 0 - конец_последовательности ’, ’ 0 ’ ); A:= StrToInt ( S ); k : = 0; for i :=1 to N do begin S:= InputBox ( ’Ввод элементов последовательности ’, ’введите число. 0 - конец последовательности ’, ’ 0 ’ ); A:= StrToInt ( S ); if ( i <>1) then if A*B<0 then k:=k+1; B:=A; end; MessageDlg ( ’K = ’+IntToStr ( k ), MtInformation, [ mbOk ], 0 ); end;
Результаты работы программы представлены на рис. 3.46, 3.47.