|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Операторы управления
Рассмотрим использование оператора if на примерах3В задачах этой главы мы не будем уделять много внимания интерфейсу создаваемых программ, чтобы у читателя была возможность разобраться в алгоритмах и способах их записи на языке Free Pascal..
 . Для функции, график которой приведён на рис. 3.10, вычислить
. Для функции, график которой приведён на рис. 3.10, вычислить  .
.Аналитически функцию, представленную на рис. 3.10, можно записать так:
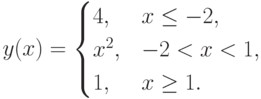
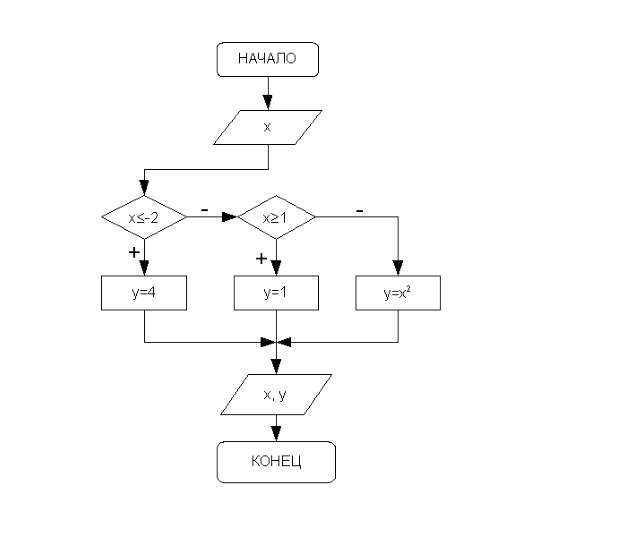
Составим словесный алгоритм решения этой задачи:
- Начало алгоритма.
- Ввод числа
 (аргумент функции).
(аргумент функции). - Если значение
 меньше либо равно -2, то переход к п. 4, иначе переход к п. 5.
меньше либо равно -2, то переход к п. 4, иначе переход к п. 5. - Вычисление значения функции:
 , переход к п. 8.
, переход к п. 8. - Если значение
 больше либо равно 1, то переход к п. 6, иначе переход к п. 7.
больше либо равно 1, то переход к п. 6, иначе переход к п. 7. - Вычисление значения функции:
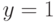 , переход к п. 8.
, переход к п. 8. - Вычисление значения функции:
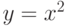 .
. - Вывод значений аргумента
 и функции
и функции  .
. - Конец алгоритма.
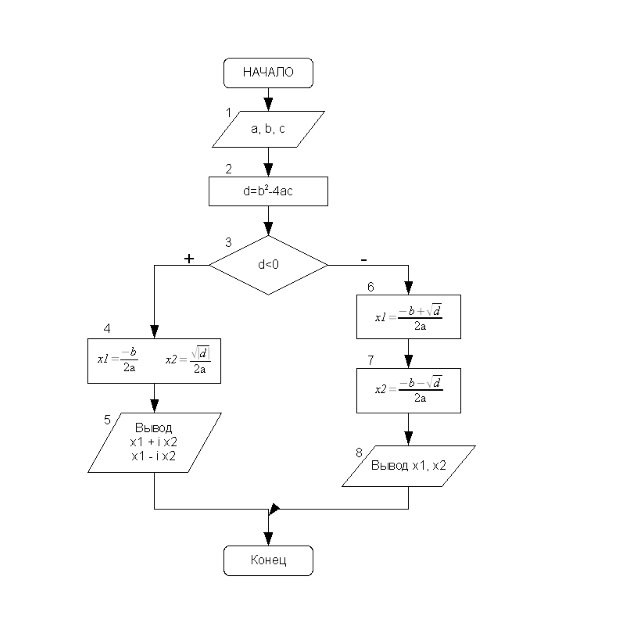
Блок-схема, соответствующая описанному алгоритму, представлена на рисунке 3.11. Как видно, блок-схема нагляднее и проще для восприятия, чем словесное описание алгоритма. В дальнейшем для описания алгоритма мы часто будем использовать именно блок-схемы.
Текст программы на языке Free Pascal будет иметь вид:
var x, y : real; begin write ( ’ x= ’ ); readln ( x ); if x<= -2 then y:=4 else if x>=1 then y:=1 else y:= sqr ( x ); writeln ( ’ x= ’, x : 5 : 2, ’ y= ’, y : 5 : 2 ); end.
Эту программу можно ввести в текстовом редакторе Geany (или в текстовом редакторе Free Pascal) и запустить на выполнение.
 и
и  . Определить, принадлежит ли точка с координатами
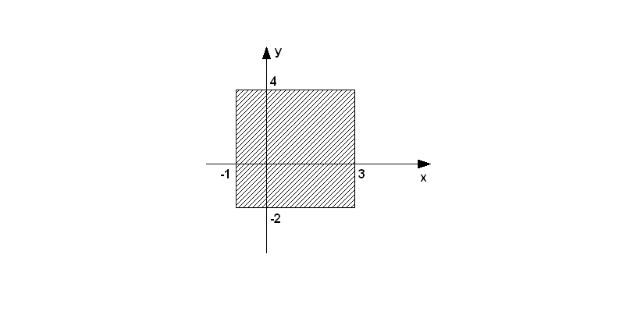
. Определить, принадлежит ли точка с координатами  заштрихованной части плоскости (рис. 3.12).
заштрихованной части плоскости (рис. 3.12).Как показано на рис. 3.12, область ограничена линиями  и
и  . Значит, точка с координатами
. Значит, точка с координатами  будет принадлежать этой области, если будут выполняться следующие условия:
будет принадлежать этой области, если будут выполняться следующие условия:  и
и 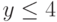 . Иначе точка лежит за пределами области.
. Иначе точка лежит за пределами области.
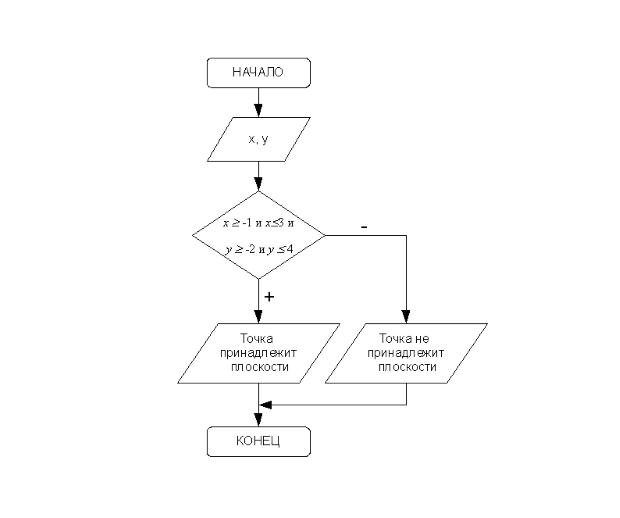
Блок-схема, описывающая алгоритм решения данной задачи, представлена на рис. 3.13.
Текст программы к задаче 3.2:
var x, y : real; begin write ( ’ x= ’ ); readln ( x ); write ( ’ y= ’ ); readln ( y ); if ( x>= -1) and ( x<=3) and ( y>= -2) and ( y<=4) then writeln ( ’Точка принадлежит области ’ ) else writeln ( ’Точка не принадлежит области ’ ); end.
Исходные данные: вещественные числа  и
и  — коэффициенты квадратного уравнения.
— коэффициенты квадратного уравнения.
Результаты работы программы: вещественные числа  и
и  — корни квадратного уравнения — либо сообщение о том, что корней нет.
— корни квадратного уравнения — либо сообщение о том, что корней нет.
Вспомогательные переменные: вещественная переменная  , в которой будет храниться дискриминант квадратного уравнения.
, в которой будет храниться дискриминант квадратного уравнения.
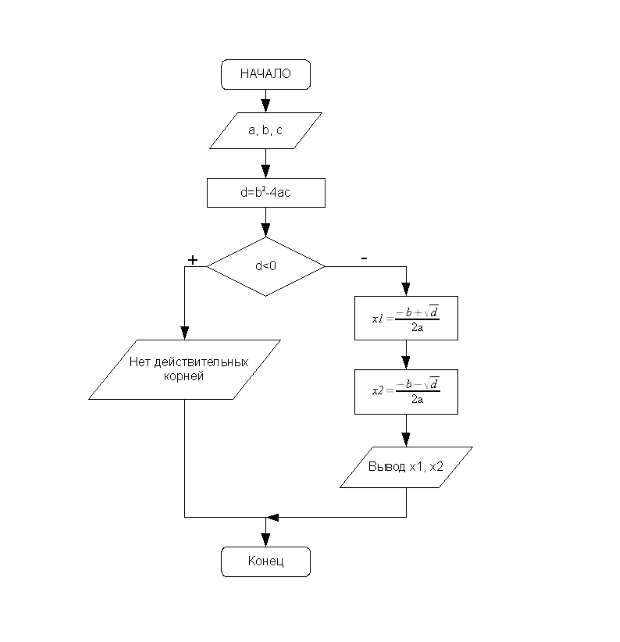
Составим словесный алгоритм решения этой задачи.
- Начало алгоритма.
- Ввод числовых значений переменных
 и
и  .
. - Вычисление значения дискриминанта
 по формуле
по формуле 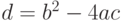 .
. - Если
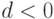 , то переход к п. 5, иначе переход к п. 6.
, то переход к п. 5, иначе переход к п. 6. - Вывод сообщения "Действительных корней нет" и переход к п. 8.
- Вычисление корней
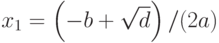 и
и 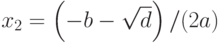 .
. - Вывод значений
 и
и  на экран.
на экран. - Конец алгоритма.
Блок-схема, соответствующая этому описанию, представлена на рис. 3.14.
Текст программы, которая реализует решение квадратного уравнения:
{Описание переменных.}
var a, b, c, d, x1, x2 : real;
begin
{Ввод значения коэффициентов квадратного уравнения.}
writeln ( ’Введите коэффициенты квадратного уравнения ’ );
readln ( a, b, c );
{Вычисление дискриминанта.}
d:=b * b-4*a*c;
{Если дискриминант отрицателен,}
if d<0 then
{то вывод сообщения, что корней нет,}
writeln ( ’Действительных корней нет ’ )
else
begin
{иначе вычисление корней x1, x2}
x1:=(-b+sqrt ( d ) ) / 2 / a;
x2:=(-b_sqrt ( d ) ) / ( 2 * a );
{и вывод их на экран.}
writeln ( ’X1= ’, x1 : 6 : 3, ’ -X2= ’, x2 : 6 : 3 )
end
end.
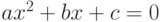 .
.Исходные данные: вещественные числа  и
и  — коэффициенты квадратного уравнения.
— коэффициенты квадратного уравнения.
Результаты работы программы: вещественные числа  и
и  — действительные корни квадратного уравнения — либо
— действительные корни квадратного уравнения — либо  и
и  — действительная и мнимая части комплексного числа.
— действительная и мнимая части комплексного числа.
Вспомогательные переменные: вещественная переменная  , в которой будет храниться дискриминант квадратного уравнения.
, в которой будет храниться дискриминант квадратного уравнения.
Можно выделить следующие этапы решения задачи:
- Ввод коэффициентов квадратного уравнения
 и
и  .
. - Вычисление дискриминанта
 по формуле
по формуле 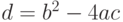 .
. - Проверка знака дискриминанта. Если
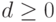 , то вычисление действительных корней:
, то вычисление действительных корней:
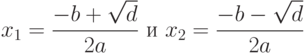
и вывод их на экран. При отрицательном дискриминанте выводится сообщение о том, что действительных корней нет, и вычисляются комплексные
корни4Комплексные числа записываются в виде 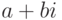 , где
, где  — действительная часть комплексного числа,
— действительная часть комплексного числа,  — мнимая часть комплексного числа,
— мнимая часть комплексного числа,  — мнимая единица
— мнимая единица 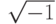 .
.
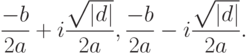
У обоих комплексных корней действительные части одинаковые, а мнимые отличаются знаком. Поэтому можно в переменной x1 хранить действительную часть числа 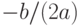 , в переменной x2 — модуль мнимой части
, в переменной x2 — модуль мнимой части 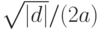 , а в качестве корней вывести x1+ix2 и x1-ix2.
, а в качестве корней вывести x1+ix2 и x1-ix2.
На рис. 3.15 изображена блок-схема решения задачи. Блок 1 предназначен для ввода коэффициентов квадратного уравнения. В блоке 2 осуществляется вычисление дискриминанта. Блок 3 осуществляет проверку знака дискриминанта; если дискриминант отрицателен, то корни комплексные, их расчёт происходит в блоке 4 (действительная часть корня записывается в переменную x1, модуль мнимой — в переменную x2), а вывод — в блоке 5 (первый корень x1+ix2, второй — x1-ix2). Если дискриминант положителен, то вычисляются действительные корни уравнения (блоки 6—7) и выводятся на экран (блок 8).
Текст программы, реализующей поставленную задачу:
var a, b, c, d, x1, x2 : real;
begin
writeln ( ’Введите_коэффициенты_квадратного_уравнения ’ );
readln ( a, b, c );
d:=b * b-4*a*c;
if d<0 then
begin
//Если дискриминант отрицателен, то вывод сообщения,
//что действительных корней нет, и вычисление комплексных корней.
writeln ( ’Действительных корней нет ’ );
{Вычисление действительной части комплексных корней.}
x1:=-b /(2 * a );
{Вычисление модуля мнимой части комплексных корней.}
x2:= sqrt ( abs ( d ) ) / ( 2 * a );
writeln ( ’Комплексные корни уравнения ’,
a : 1 : 2, ’ x^2+ ’, b : 1 : 2, ’ x+ ’, c : 1 : 2, ’=0 ’ );
{Вывод значений комплексных корней в виде 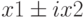 }
writeln ( x1 : 1 : 2, ’+i * ( ’, x2 : 1 : 2, ’ ) ’ );
writeln ( x1 : 1 : 2, ’- i * ( ’, x2 : 1 : 2, ’ ) ’ );
end
else
begin
{иначе вычисление действительных корней x1, x2}
x1:=(-b+sqrt ( d ) ) / 2 / a;
x2:=(-b_sqrt ( d ) ) / ( 2 * a );
{и вывод их на экран.}
writeln ( ’Действительные корни уравнения ’,
a : 1 : 2, ’ x^2+ ’, b : 1 : 2, ’ x+ ’, c : 1 : 2, ’=0 ’ );
writeln ( ’X1= ’, x1 : 1 : 2, ’ X2= ’, x2 : 1 : 2 )
end
end.
}
writeln ( x1 : 1 : 2, ’+i * ( ’, x2 : 1 : 2, ’ ) ’ );
writeln ( x1 : 1 : 2, ’- i * ( ’, x2 : 1 : 2, ’ ) ’ );
end
else
begin
{иначе вычисление действительных корней x1, x2}
x1:=(-b+sqrt ( d ) ) / 2 / a;
x2:=(-b_sqrt ( d ) ) / ( 2 * a );
{и вывод их на экран.}
writeln ( ’Действительные корни уравнения ’,
a : 1 : 2, ’ x^2+ ’, b : 1 : 2, ’ x+ ’, c : 1 : 2, ’=0 ’ );
writeln ( ’X1= ’, x1 : 1 : 2, ’ X2= ’, x2 : 1 : 2 )
end
end.
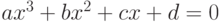 .
.Кубическое уравнение имеет вид
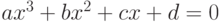 |
( 3.1) |
После деления на  уравнение (3.1) принимает канонический вид:
уравнение (3.1) принимает канонический вид:
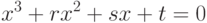 |
( 3.2) |
где 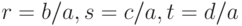 . В уравнении (3.2) сделаем замену
. В уравнении (3.2) сделаем замену  и получим приведённое уравнение:
и получим приведённое уравнение:
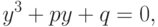 |
( 3.3) |
где
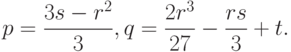
Число действительных корней приведённого уравнения (3.3) зависит от знака дискриминанта  приведённого кубического уравнения (табл. 3.1).
приведённого кубического уравнения (табл. 3.1).
| Дискриминант | Количество действительных корней | Количество комплексных корней |
|---|---|---|
| D > 0 | 1 | 2 |
| D < 0 | 3 | — |
Корни приведённого уравнения могут быть рассчитаны по формулам Кардано:
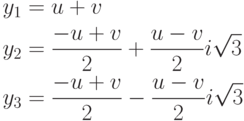 |
( 3.4) |
где
![u=\sqrt[{3}]{-q/2+\sqrt{D}},
v=\sqrt[{3}]{-q/2-\sqrt{D}}.](/sites/default/files/tex_cache/07c9f04959152de706cbe193863a3b52.png)
При отрицательном дискриминанте уравнение (3.1) имеет три действительных корня, но они будут вычисляться через вспомогательные комплексные величины. Чтобы избавиться от этого, можно воспользоваться формулами:
![\begin{aligned}
y_1&=2\sqrt[3]{\rho}\cos\left(\frac{\varphi}{3}\right),\\
y_2&=2\sqrt[3]{\rho}\cos\left(\frac{\varphi}{3}+\frac{2\pi}{3}\right),\\
y_3&=2\sqrt[3]{\rho}\cos\left(\frac{\varphi}{3}+\frac{4\pi}{3}\right),
\end{aligned}](/sites/default/files/tex_cache/b02aa659a0a5b0d307b5b416331d192b.png) |
( 3.5) |
где
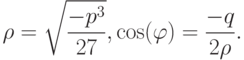
Таким образом, при положительном дискриминанте кубического уравнения (3.3) расчёт корней будем вести по формулам (3.4), а при отрицательном — по формулам (3.5).
После расчёта корней приведённого уравнения (3.3) по формулам (3.4) или (3.5) необходимо по формулам
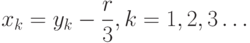
перейти к корням заданного кубического уравнения (3.1).
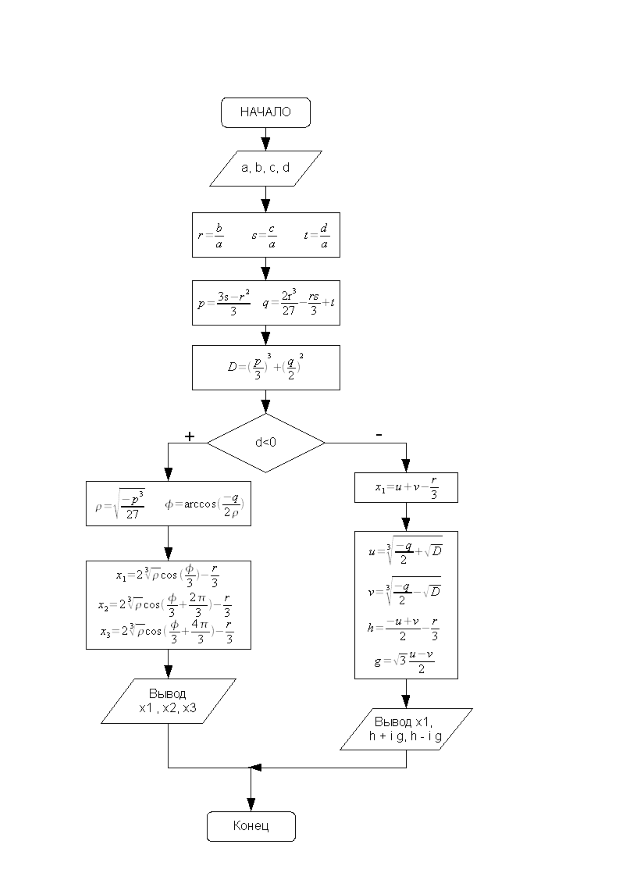
Блок-схема решения кубического уравнения представлена на рис. 3.16.
Описание блок-схемы. В блоке 1 вводятся коэффициенты кубического уравнения, в блоках 2—3 рассчитываются коэффициенты канонического и приведённого уравнений. Блок 4 предназначен для вычисления дискриминанта. В блоке 5 проверяется знак дискриминанта кубического уравнения. Если он отрицателен, то корни вычисляются по формулам (3.5) (блоки 6—7). При положительном значении дискриминанта расчёт идет по формулам (3.4) (блок 9, 10). Блоки 8 и 11 предназначены для вывода результатов на экран.
Текст программы с комментариями приведён
ниже55При расчёте величин  и
и  в программе предусмотрена проверка значения подкоренного выражения. Если
в программе предусмотрена проверка значения подкоренного выражения. Если  , то
, то ![u=\sqrt[3]{\frac{-q}{2}+ \sqrt{D}} > 0](/sites/default/files/tex_cache/d6adb68945a82eef5dc8b8e758a5b659.png) , а
, а ![v=\sqrt[3]{\frac{-q}{2}- \sqrt{D}} > 0](/sites/default/files/tex_cache/880c7c8fae4cbe4e1a2c07e744b96166.png) . Если
. Если
 , то
, то
![u=\sqrt[3]{\frac{-q}{2}+ \sqrt{D}} > 0](/sites/default/files/tex_cache/d6adb68945a82eef5dc8b8e758a5b659.png) , а
, а ![v=\sqrt[3]{\frac{-q}{2}- \sqrt{D}} > 0](/sites/default/files/tex_cache/880c7c8fae4cbe4e1a2c07e744b96166.png) . Соответственно, при нулевом значении подкоренного выражения
. Соответственно, при нулевом значении подкоренного выражения  и
и  обращаются в ноль..
обращаются в ноль..
var a, b, c, d, r, s, t, p, q, ro, f i, x1, x2, x3, u, v, h, g : real; begin //Ввод коэффициентов кубического уравнения. write ( ’ a= ’ ); readln ( a ); write ( ’ b= ’ ); readln ( b ); write ( ’ c= ’ ); readln ( c ); write ( ’ d= ’ ); readln ( d ); //Расчёт коэффициентов канонического уравнения по 3.2. r :=b/a; s := c /a; t :=d/a; //Вычисление коэффициентов приведённого уравнения 3.3. p :=(3 * s - r * r ) / 3; q:=2* r * r * r /27- r * s/3+ t; //Вычисление дискриминанта кубического уравнения. d :=( p /3) * sqr ( p/3)+ sqr ( q / 2 ); //Проверка знака дискриминанта, //ветка then реализует формулы (3.5), //ветка else — формулы 3.4 if d<0 then begin ro := sqrt (-p * p * p / 27 ); //Следующие два оператора реализуют расчёт угла fi, //сначала вычисляется величина косинуса угла, //затем вычисляется его арккосинус через арктангенс. fi :=-q /(2 * ro ); fi := pi /2-arctan ( fi / sqrt (1 - fi * fi ) ); //Вычисление действительных корней уравнения x1, x2 и x3 x1 :=2 * exp (1/3 * ln ( ro ) ) * cos ( fi /3) - r / 3; x2 :=2 * exp (1/3 * ln ( ro ) ) * cos ( fi /3+2 * pi /3) - r / 3; x3 :=2 * exp (1/3 * ln ( ro ) ) * cos ( fi /3+4 * pi /3) - r / 3; writeln ( ’ x1= ’, x1 : 1 : 3, ’ x2= ’, x2 : 1 : 3, ’ x3= ’, x3 : 1 : 3 ); end else begin //Вычисление u и v с проверкой знака // подкоренного выражения. if -q/2+ sqrt ( d)>0 then u:=exp (1/3 * ln (-q/2+ sqrt ( d ) ) ) else if -q/2+ sqrt ( d)<0 then u:=-exp (1/3 * ln ( abs(-q/2+ sqrt ( d ) ) ) ) else u : = 0; if -q/2- sqrt ( d)>0 then v:=exp (1/3 * ln (-q/2- sqrt ( d ) ) ) else if -q/2- sqrt ( d)<0 then v:=-exp (1/3 * ln ( abs(-q/2- sqrt ( d ) ) ) ) else v : = 0; //Вычисление действительного корня кубического уравнения. x1:=u+v-r / 3; //Вычисление действительной и // мнимой части комплексных корней. h:=-(u+v)/2 - r / 3; g :=(u - v )/2 * sqrt ( 3 ); writeln ( ’ x1= ’, x1 : 1 : 3, ’ x2= ’, h : 1 : 3, ’+i* ’, g : 1 : 3, ’ x3= ’, h : 1 : 3, ’ -i* ’, g : 1 : 3 ); end end.
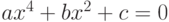 . Найти все его действительные корни.
. Найти все его действительные корни.Входные данные: a, b, c. Выходные данные: x1, x2, x3, x4.
Для решения биквадратного уравнения необходимо заменой 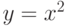 привести его к квадратному уравнению
привести его к квадратному уравнению 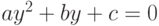 и решить это уравнение.
и решить это уравнение.
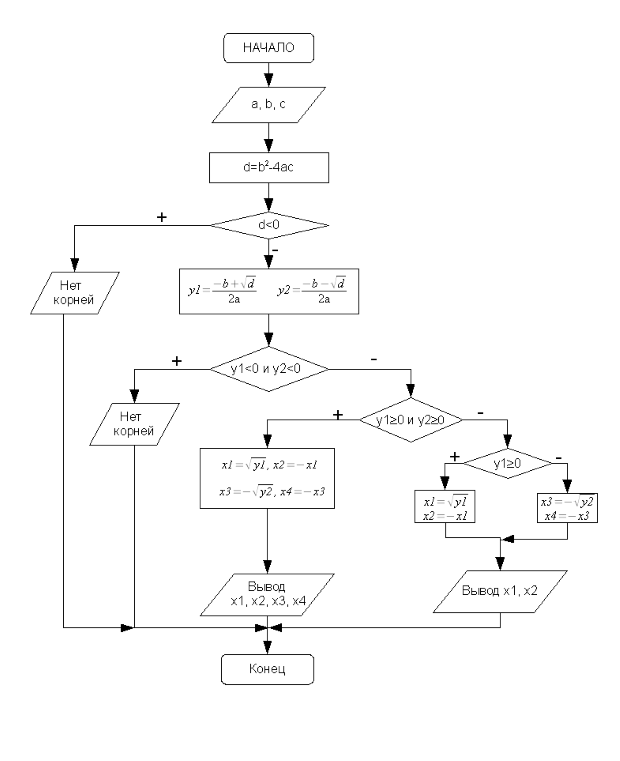
Опишем алгоритм решения этой задачи (рис. 3.17):
- Ввод коэффициентов биквадратного уравнения
 и
и  (блок 1).
(блок 1). - Вычисление дискриминанта уравнения
 (блок 2).
(блок 2). - Если
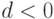 (блок 3), вывод сообщения, что корней нет (блок 4), а иначе определяются корни соответствующего квадратного уравнения
(блок 3), вывод сообщения, что корней нет (блок 4), а иначе определяются корни соответствующего квадратного уравнения 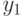 и
и 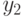 (блок 5).
(блок 5). - Если
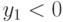 и
и 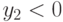 (блок 6), то вывод сообщения, что корней нет (блок 7).
(блок 6), то вывод сообщения, что корней нет (блок 7). - Если
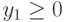 и
и 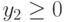 (блок 8), то вычисляются четыре корня по формулам
(блок 8), то вычисляются четыре корня по формулам 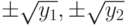 (блок 9) и выводятся значения корней (блок 10).
(блок 9) и выводятся значения корней (блок 10). - Если условия 4) и 5) не выполняются, то необходимо проверить знак
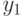 . Если
. Если 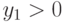 (блок 11), то вычисляются два корня по формуле
(блок 11), то вычисляются два корня по формуле 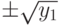 (блок 12), иначе (если
(блок 12), иначе (если 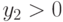 ) вычисляются два корня по формуле
) вычисляются два корня по формуле 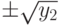 (блок 13).
(блок 13). - Вывод вычисленных значений корней (блок 14).
Текст программы на языке Free Pascal с комментариями:
//Описание переменных: //a,b,c - коэффициенты биквадратного уравнения, //d - дискриминант, //x1,x2,x3,x4 - корни биквадратного уравнения, //y1,y2 - корни квадратного уравнения ay^2+by+c=0. var a, b, c, d, x1, x2, x3, x4, y1, y2 : real; begin //Ввод коэффициентов уравнения. writeln ( ’Введите коэффициенты биквадратного уравнения ’ ); readln ( a, b, c ); //Вычисление дискриминанта. d:=b * b-4*a*c; //Если он отрицателен, if d<0 then //вывод сообщения "Корней нет" writeln ( ’Корней нет ’ ) //Если дискриминант >= 0, else begin //вычисление корней квадратного уравнения. y1:=(-b+sqrt ( d ) ) / 2 / a; y2:=(-b-sqrt ( d ) ) / ( 2 * a ); //Если оба корня квадратного уравнения < 0, if ( y1 <0) and ( y2 <0) then //вывод сообщения "Корней нет". writeln ( ’Корней нет ’ ) //Если оба корня квадратного уравнения >= 0, else if ( y1>=0) and ( y2>=0) then begin //вычисление четырех корней биквадратного уравнения. x1:= sqrt ( y1 ); x2:=-x1; x3:= sqrt ( y2 ); x4:=-sqrt ( y2 ); //Вывод корней биквадратного уравнения на экран. writeln ( ’X1= ’, x1 : 6 : 3, ’ X2= ’, x2 : 6 : 3 ); writeln ( ’X3= ’, x3 : 6 : 3, ’ X4= ’, x4 : 6 : 3 ); end //Если не выполнились оба условия // 1. y1<0 И y2<0 // 2. y1>=0 И y2>=0, //то проверяем условие y1>=0 else if ( y1>=0) then //Если оно истинно begin x1:= sqrt ( y1 ); x2:=-x1; writeln ( ’X1= ’, x1 : 6 : 3, ’ X2= ’, x2 : 6 : 3 ); end else //Если условие y1>=0 ложно, то begin x1:= sqrt ( y2 ); x2:=-x1; writeln ( ’X1= ’, x1 : 6 : 3, ’ X2= ’, x2 : 6 : 3 ); end end end.