Обрамление Maxima
5.3 Интегрированная среда Sage
Sage (англ. "Мудрец") — система компьютерной алгебры покрывающая много областей математики, включая алгебру, комбинаторику, вычислительную математику и матанализ. Первая версия Sage была выпущена 24 февраля 2005 года в виде свободного программного обеспечения с лицензией GNU GPL. Первоначальной целью проекта было "создание открытого программного обеспечения альтернативного системам Magma, Maple, Mathematica, и MATLAB". Разработчиком Sage является Уильям Стейн — математик Университета Вашингтона (Официальный сайт: http://sagemath.org).
Многочисленные возможности Sage включают:
- Интерфейс notebook для просмотра и повторного использования введённых команд и полученных результатов, включая графики и текстовые аннотации, доступный из большинства современных веб-браузеров. Доступно защищённое соединение через протокол HTTPS, когда конфиденциальность имеет значение. Так же Sage может выполняться как локально, так и удалённо.
- Интерфейс ввода на основе командной строки, с использованием мультипарадигменного языка IPython.
- Поддержка параллельных вычислений с использованием как многоядерных процессоров, так и многопроцессорных систем и систем распределённых вычислений.
- Внутренняя инфраструктура на python, поддерживающая взаимодействие с математическими пакетами на python: SymPy, SciPy и NumPy.
- Различные статистические библиотеки функций, использующие функциональность R и SciPy.
- Возможность построения плоских и трёхмерных графиков для функций и данных.
- Средства работы с матрицами и массивами данных с поддержкой разрежённых массивов.
- Набор инструментов для добавления собственного пользовательского интерфейса к вычислениям и приложениям.
- Сетевые инструменты для соединения с базами данных SQL, поддержка сетевых протоколов, включая HTTP, NNTP, IMAP, SSH, IRC, FTP.
Sage — сам по себе мощное средство благодаря многочисленным объектно-ориентированным возможностям и большому объёму возможностей, реализованному на python для решения всевозможных задач. Однако следует учитывать, что основная идея Sage — интеграция всевозможных математических пакетов, как открытых, так и проприетарных. Наряду с функцией интеграции, Sage включает достаточно развитые собственные возможности — многочисленные функции и структуры данных. Преобразование результатов, полученных, например, в Maxima, к структурам Sage может оказаться достаточно сложной задачей.
5.4 Построение графических иллюстраций: пакет draw
В Maxima имеется несколько альтернативных библиотек для отображения графиков функций, наборов точек, трехмерных тел, градиентов и т.д. По умолчанию используется библиотека Plot, но для решения некоторых задач может оказаться удобнее библиотека Draw.
Варианты использования команды plot2d рассмотрены выше, поэтому ниже иллюстрируются возможности draw. Библиотека draw построена на интерфейсе Maxima-gnuplot. Библиотека включает три основные функции, доступные на уровне Maxima: draw2d, draw3d,draw. Перед использованием draw необходимо загрузить командой load("draw").
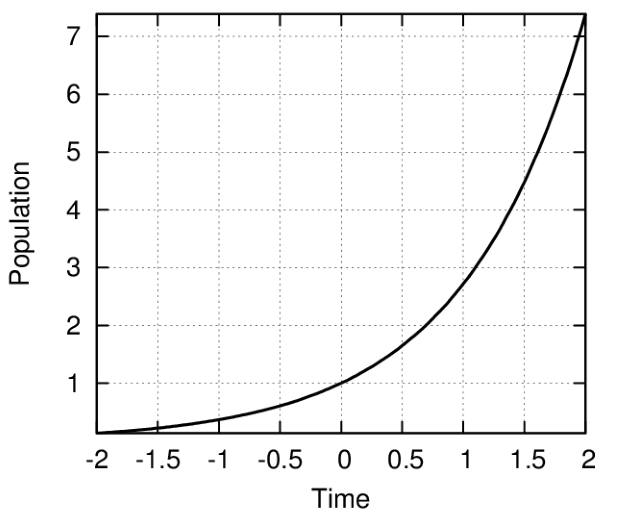
Рассмотрим несложный пример. На графике (рис. 5.15) показана кривая 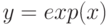 . График построен с использованием функции
. График построен с использованием функции  . Функции, заданные явно, указываются командой
. Функции, заданные явно, указываются командой 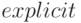 . Для каждой функции указывается имя переменной и пределы изменения абсциссы. Пределы ординаты выбираются автоматически. Команда построения графика:
. Для каждой функции указывается имя переменной и пределы изменения абсциссы. Пределы ординаты выбираются автоматически. Команда построения графика:
(%i4) draw2d(grid=true,xlabel = "Time", ylabel = "Population", explicit(exp(u),u,-2,2))$
На графике показана сетка (grid=true), а также метки осей (xlabel и ylabel).
Вывод графика на печать организуется при помощи указания типа терминала. Возможные варианты — screen (экран по умолчанию), png, jpg, eps, eps_color, gif, animated_gif, wxt, aquaterm.
Команда для вывода графика на печать имеет вид (указан терминал eps — encapsulated postscript):
(%i6) draw2d(terminal=eps,grid=true,xlabel = "Time", ylabel = "Population", explicit(exp(u),u,-2,2))$
По умолчанию рисунок сохраняется в файл maxima_out.eps; указание имени файла для вывода осуществляется командой file_name ="имя файла".
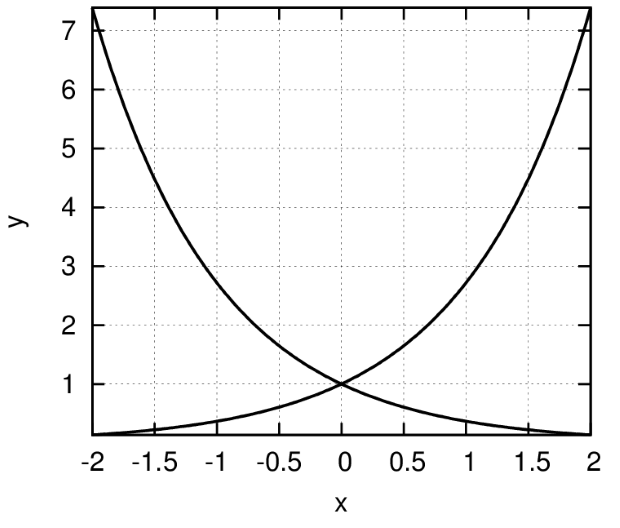
Построим аналогичный график (рис. 5.16), но с выводом кривых  и
и 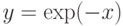 в одних осях c сохранением графика в файл draw_2.eps. Необходимая команда:
в одних осях c сохранением графика в файл draw_2.eps. Необходимая команда:
(%i7) draw2d(terminal=eps, file_name="draw_2",grid=true, xlabel = "x",ylabel = "y",explicit(exp(u),u,-2,2), explicit(exp(-u),u,-2,2))$
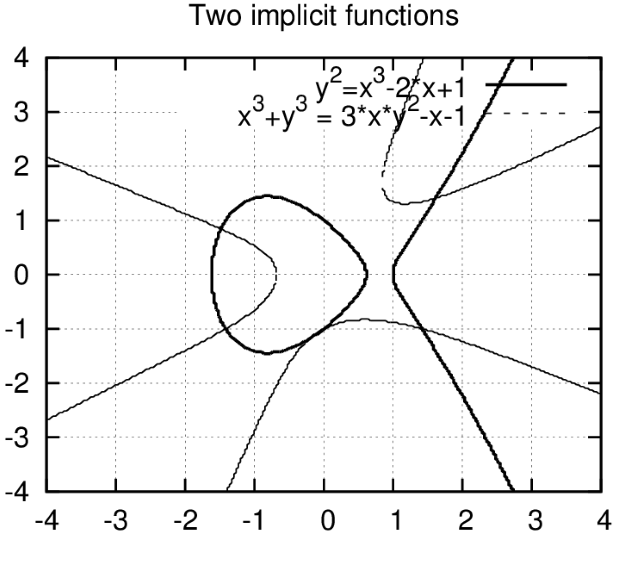
С помощью пакета draw можно строить и графики функций, заданных неявно. В этом случае функция задаётся командой implicit, например (результат построения — на рис. 5.17):
(%i1) load(draw)$ (%i2) draw2d(grid = true, title = "Two implicit functions", line_type = solid, key = "y^2=x^3-2*x+1", implicit(y^2=x^3-2*x+1, x, -4,4, y, -4,4), line_type = dots, key = "x^3+y^3 = 3*x*y^2-x-1", implicit(x^3+y^3 = 3*x*y^2-x-1, x,-4,4, y,-4,4))$
На графике хорошо видно, что кривые проведены разными линиями (одна сплошная, другая точечная). Для указания типа линии использована опция line_type=тип линии (возможные значения — solid и dots).
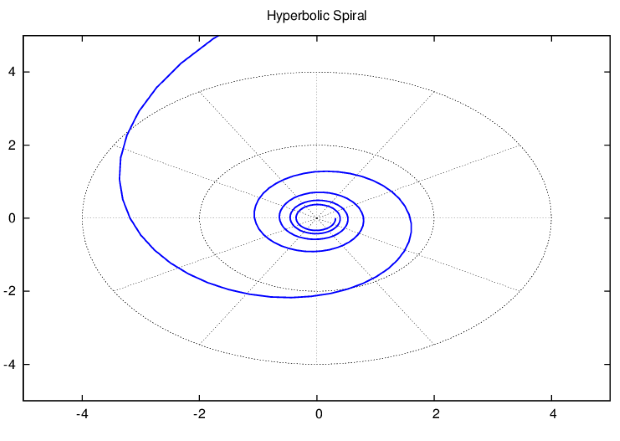
Помимо графиков неявных функций, при помощи draw могут быть построены и графики параметрических функций или функций, заданных в полярных координатах. В этих случаях вместо команд explicit или implicit используются команды parametric и polar соответственно. Пример графика функции в полярных координатах — на рис. 5.18. Соответствующая команда:
draw2d(user_preamble = "set grid polar", nticks = 200, xrange = [-5,5], yrange = [-5,5], color = blue, line_width = 3, title = "Hyperbolic Spiral", polar(10/theta,theta,1,10*%pi))$
В последнем примере указаны параметры построения графика: интервалы изменения  и
и  , равные xrange и yrange, толщина линии line_width и её цвет color. Кроме того, важным параметром является опция user_preamble. Эта опция указывает команды gnuplot, определённые пользователем и выполняющиеся перед построением данного графика.
, равные xrange и yrange, толщина линии line_width и её цвет color. Кроме того, важным параметром является опция user_preamble. Эта опция указывает команды gnuplot, определённые пользователем и выполняющиеся перед построением данного графика.
Для использования меток осей и заголовков на русском языке необходимо в user_preamble или в специальном файле .gnuplot (этот файл содержит команды gnuplot, выполняющиеся при старте программы) указать русскую кодировку командой set encoding koi8r или украинскую кодировку set encoding koi8u. Кроме того, часто оказывается необходимым указать и шрифт для вывода заголовка или меток.
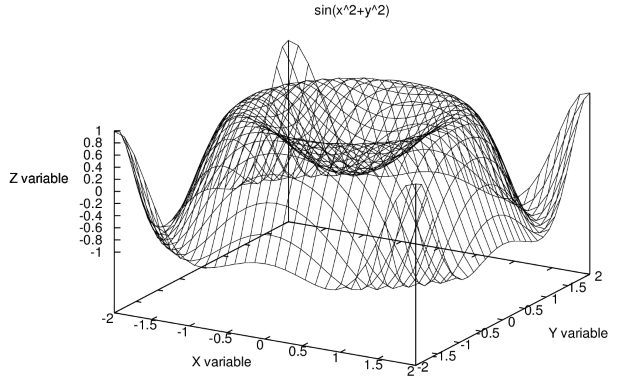
Функция  позволяет строить трёхмерные графики. При- мер:
позволяет строить трёхмерные графики. При- мер:
(%i8) draw3d(zlabel = "Z variable",ylabel = "Y variable", explicit(sin(x^2+y^2),x,-2,2,y,-2,2), xlabel="X variable")$
Метка оси  указывается командой zlabel=имя. Вывод графика на печать аналогичен указанному выше. Пример (с указанием, помимо меток осей, и названия графика командой title=имя) приведен на рис. 5.19.
указывается командой zlabel=имя. Вывод графика на печать аналогичен указанному выше. Пример (с указанием, помимо меток осей, и названия графика командой title=имя) приведен на рис. 5.19.
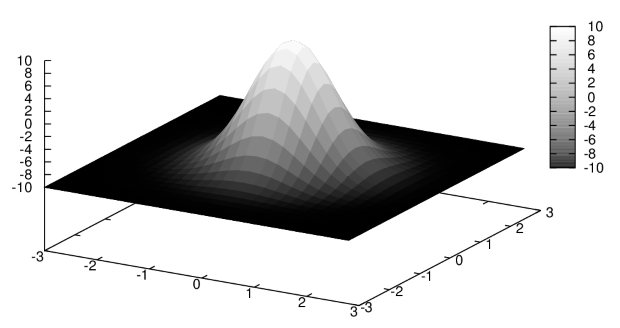
Очевидно, что при помощи функции  , можно строить и окрашенные поверхности (либо полутоновые). Для этого в качестве аргумента функции
, можно строить и окрашенные поверхности (либо полутоновые). Для этого в качестве аргумента функции  указывается опции
указывается опции 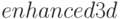 (указывает на построение трёхмерной окрашенной поверхность) и
(указывает на построение трёхмерной окрашенной поверхность) и  (palette=color — цветная поверхность, palette=gray — оттенки серого). Пример поверхности, окрашенной оттенками серого — на рис. 5.20. Необходимая команда:
(palette=color — цветная поверхность, palette=gray — оттенки серого). Пример поверхности, окрашенной оттенками серого — на рис. 5.20. Необходимая команда:
(%i12) draw3d(terminal=eps,surface_hide = true, enhanced3d = true, palette=gray, explicit(20*exp(-x^2-y^2)-10,x,-3,3,y,-3,3))$
Пакет draw позволяет и строить несколько графиков на одном рисунке, а также предоставляет ряд других полезных возможностей, но для их использования необходимо ознакомиться с документацией, поставляемой с пакетом Maxima.