Цифровая модуляция

Отображение сверточного кода (решетчатая диаграмма)

Рассмотрим теперь кодер изображенный на рис 4.16б. Он содержит три накопителя (триггера), которые определяют вид кода на выходе. При этом первый триггер содержит входной сигнал. Попробуем отобразить переходы в такой схеме от одного состояния к другому, при поступлении следующего входного двоичного сигнала (значения 0 или 1) с помощью двоичного дерева. При этом можно использовать показанные выше результаты преобразования входной выходную последовательность.

Решетчатой диаграммой XE "Решетчатой диаграммой" называется ориентированный граф с периодически повторяющейся структурой "ячеек". Каждая ячейка содержит колонки из одинакового числа вершин (узлов), соединенных ребрами. Между процедурой кодирования сверточным кодом и решеткой имеется взаимно однозначное соответствие, которое задается следующими правилами:

1. Исходное положение диаграммы.
   • слева перечисляются все возможные комбинации из 3 символов;
   • ниже (в квадратных скобках) приведен результат обработки это комбинации в соответствии с заданным алгоритмом;
   • комбинация их двух символов, которая может быть добавлена следующим символом исходной последовательности, при смещении влево.

Построение дерева ( рис. 4.19а).

увеличить изображение
Рис. 4.20. Диаграмма (решетка) согласно алгоритму по рис.4.18б

После установки исходных данных строится дерево (решетка). Она строится по ступеням.

• Из каждой вершины исходных данных рисуется граф с двумя ветвями – ветвь, исходящая из каждой вершины, соответствует одному из возможных символов источника (для двоичного источника из каждой вершины выходит два ребра – верхнее для 0 и нижнее для 1);
• каждая вершина (узел) соответствует внутреннему состоянию кодера (двум символам остающимися без изменений);
• над каждым ребром отмечены значения символов (в данном случае двоичных 0 или 1), поступающих от источника,
• далее над ребром написан получаемая комбинация, а под ней в квадратных скобках результат обработки этой комбинации.

Используя рис. 4.19и получаемую исходную последовательность можно определить последовательности кодов, передаваемых в линию. На этом рисунке жирным шрифтом показаны значения, получаемые при приеме исходной последовательности, приведенной на рис.4.18б. Ниже приводится пример использования решетчатых кодов совместно с ФМ –модуляцией [ 2 ] , [ 69 ]

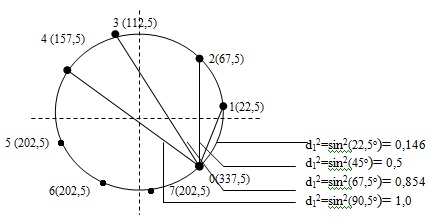
На рис.4.20 показаны сигнальные точки и запасы помехоустойчивости. Предполгается, что запас гарантируется при сдвиге фазы не более чем наполовину расстояния от данной нулевой точки Это значение 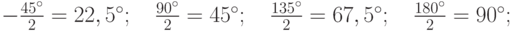. Запас по мощности пропорционален этим расстояниям.

В решетке между двумя точками может быть выбран один из двух переходов. Каждый из переходов кодируется двумя символами (см свертончый код). Сигналы передаются в течении трех интервалов (состояний).

Рис. 4.21. Сигнальные точки и запасы помехоустойчивости из четырех состояний для модуляции 8-ФМ

Рис. 4.22. Решетка с четырьмя состояниями для модуляции методом 8-ФМ

Обычно при реализации метода используется избыточное число сигнальных точек. При этом накладываются ограничения на последовательность их следования. Разрешенный порядок следования показан с помощью решетки. Поэтому применяется термин модуляция с решетчатым кодированием XE "модуляция с решетчатым кодированием" (Trellis Coded Modulation - TCM).

Алгоритм детектирования определяет наиболее вероятную последовательность состояний передаваемых кодов. В качестве примера рассмотрим расширение модуляции 4 –ФМ до 8-ФМ, как это показано на рис 4.20 . Несмотря на то, что в сигнально-точечном представлении 8-ФМ есть 8 точек в каждом интервале, но могут свободно выбираться только четыре из них. Какие именно точки будут выбраны, зависит от точек, выбранных в предыдущем интервале. При получении сигнала приемником (демодулятором) перед принятием решения о закодированных данных определяется, какая из допустимых последовательностей сигналов наиболее близка к принятой последовательности (см. пример).

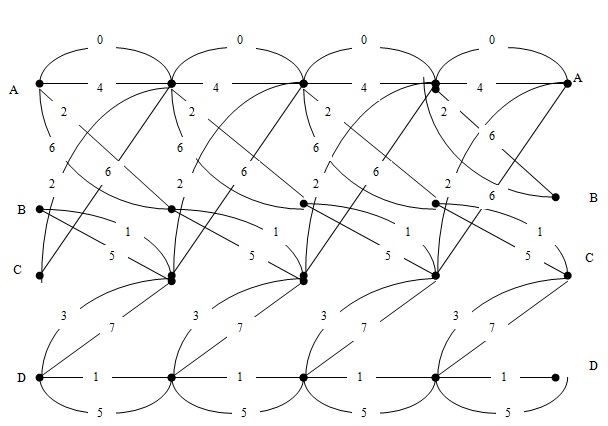
На рисунке также показан предел помехоустойчивости, (порог чувствительности, определяемый уровнем собственных шумов приемника в отсутствии полезного сигнала). Решетка XE "Решетка" переходов , изображенна на рис.4.21 .

Важно отметить, что на рисунке приведены не сигналы, а переходы из одного состояния в другое.Переходы кодируются двумя битами . Еще раз подчеркнем, что из предложенных 8-ми точек выбираются четыре. Основные принципы декодирования состоят в следующем.

• Разрешенный переход осуществляться для любых двух сигналов любыми сигналами даже если их последовательность не позволяет их распознование. Однако, эти два сигнала выбираются так, чтобы получить максимальное разделение (запас по шуму равен 1), поэтому введение избыточности становится ненужной.
• Переходы, начинающиеся в разных состояниях и заканчивающиеся в некотором одном конкретном состоянии, кодируются сигналами, имеющими предел помехоустойчивости по шуму равный или больший 0,5.
• Все последовательности, которые начинаются и заканчиваются в одних и тех же состояниях, имеют длительность как минимум три интервала с минимальным запасом помехоустойчивости по шуму равным или больше 0,5; 0,146; 0,5 Таким образом общая помехоустойчивость по шуму между двумя любыми последовательностями минималной длины равен 1,146.

Упражнение. 4.1. Приемник в системе TCM ( рис. 4.20) обнаружил последовательность фаз Определить допустимую последовательность трех сигналов, расстояние которых до принятой последовательности было минимальным. Принять за начальную точку .

Решение.

Вначале мы можем определить ближайшие фазы кодированного сигнала, которые соответствуют сигнальным точках 1,5 и 1. Анализ рис.4.21 показывает, что такая последовательность недопустима, так как сигнал 5 не может следовать за сигналом 1. Если бы принятие решений проходило символ за символом, то наверняка была бы сделана ошибка. Просматривая решетку, начиная с точки , получим набор разрешенных последовательностей, приведенный табл.4.4 . Для каждого перехода показа наиболе вероятный сигнал, который может образовать переход. В таблице также указаны отклонения каждого сигнала от принятого (в градусах), а также суммарная ошибка последовательности. Как видно, наиболее подходящая последовательность . (последовательность сигналов 1,6,0).

Переход

Суммарная ошибка при этом равна

Таблица показывает, что можно выбрать другие последовательности (141 и 162), также близкие к максимально правдподобной последовательности сигналов. Отметим, что конечные состояния этих последовательностей ( и ) отличаются от конечного состояния выбранной последовательности. Так как состояния и , не имеют общих разрешенных сигналов, следующий символ позволит вновь вернуться к выбору между последовательностями 160 и 162. Ближайший сигнал не поможет выбору между 160 и 141, а следующий за ним сигнал позволит принять решение.

Для строгого определения наиболее подходящей последовательности передаваемых сигналов необходимо рассматривать другие начальные состояния ( а не только как в упражнении состояние ).