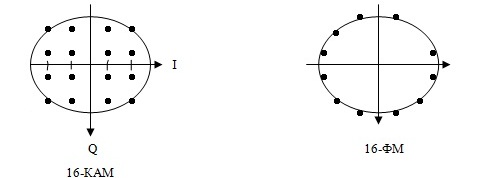
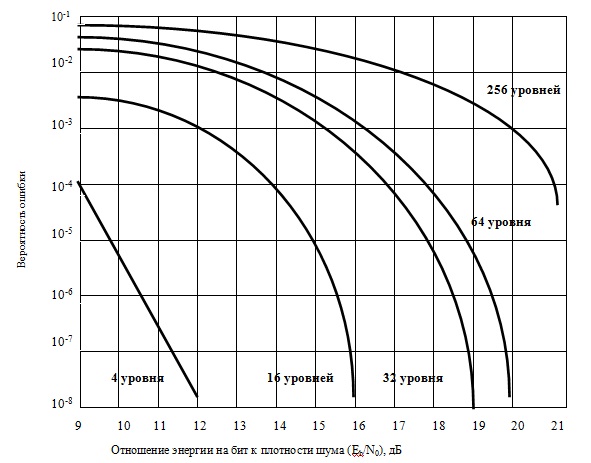
Цифровая модуляция

Восстановление на приемном конце опорных колебаний и тактовой частоты.

Как мы видели на примерах, реализации демодуляторов требуется наличие местного опорного колебания синхронизированного с передатчиком. Более того, для многоуровневых систем требуется, как правило, и дополнительное опорное колебание в квадратуре к первому. В данном случае восстановление любого опорного колебания осложняется тем, что ФМ в отличие от других видов модуляции в спектре, передаваемого сигнала, не имеет канала, по которому можно передать несущую частоту передатчика. Отсутствие несущей может быть преодолено с помощью методов нелинейного преобразования [ 75 ]

Спектр сигналов ФМ и характеристики ошибок

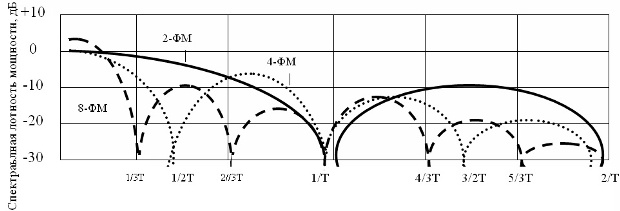
На рис.4.8 приведены для сравнения спектры сигналов для систем 2-ФМ, 4-ФМ, 8-ФМ, рассчитанных на одинаковые скорости передачи данных.

Напомним, что для системы ИКМ 90% мощности содержится в полосе спектра ( –длительность символа исходного сигнала). Высокий процент мощности внутри этой полосы означает, что сигнал может быть заключен в полосе до , и давать хорошую аппроксимацию идеальной формы сигнала.

увеличить изображение
Рис. 4.9. Спектр нефильтрованных сигналов с ФМ на одинаковой скорости передачи

На рис.4.8 видно, что более многоуровневые системы работают при более узком спектре (при более низких скоростях передачи символов, но не битов исходных данных). Так система 8-ФМ передает один символ, содержащий 3 – бита (см. рис. 4.1 ), но имеет спектр в 3 раза меньше чем ИКМ ().

Теоретически для удобного восстановления требуется сохранить характеристики в середине каждого интервала. Поэтому требуемая ширина полосы частот равна 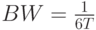. Или скорость передачи информации в данной полосе частот равна

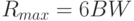
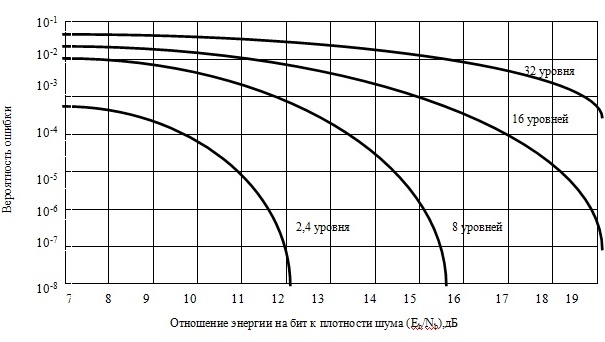
Характеристика ошибок приведена на рис.4.9 .

Чем больше уровней в системе тем, больше нужно иметь отношение энергии на бит к плотности шума (коэффициент сигнал-шум) при равной вероятности ошибки. Например, для получения одной и той же вероятности ошибки для систем 4-ФМ и 8- ФМ требуется для 8-ФМ повысить коэффициент сигнал-шум на 3 дБ.

Рис. 4.10. Вероятности ошибок в системе с ФМ

Базовое выражение, определяющее расстояние между соседними точкам в многоуровневой системе с ФМ, имеет вид:

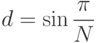( 4.6)

Квадратурно–амплитудная модуляция

Как видно из предыдущих разделов, использование квадратурных сигналов удобно для представления фазовой модуляции с четырьмя и более фазами. В случае 4 ФМ квадратурные сигналы соответствуют отдельным каналам из-за того, что для каждого квадратурного канала первичный сигнал может рассматриваться независимо. В многоуровневых системах с ФМ уровень исходного сигнала для канала I не является независимым от уровня канала Q (см. рис.4.4 и табл. 4.2 ). После приема первичного сигнала, однако, процессы модуляции и демодуляции могут рассматриваться как независимые для всех систем с ФМ.

Квадратурно-амплитудная модуляция - КАМ (QAM – Quadrature Amplitude Modulation) может рассматриваться как расширенная многоуровневая ФМ, в которой два исходных сигнала генерируются независимо. Таким образом, здесь имеют место два полностью независимых квадратурных канала, включающие процессы кодирования и детектирования в основной полосе.

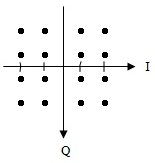
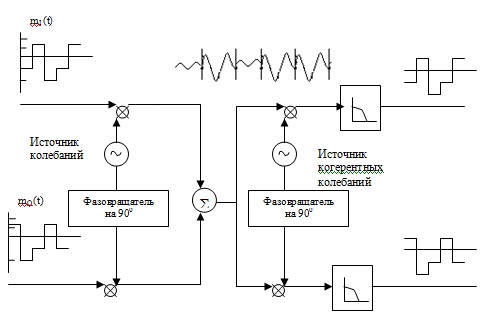
На рис.4.11 показано сигнально - точеное пространство для системы с 16-КАМ и четырмя уровнями в каждом квадратурном канале. Точки представляют составной сигнал, а штрихи на осях отмечают уровни амплитуды в каждом квадратурном канале. Основная схема модулятор – демодулятора 16-КАМ представлена на рис.4.12 .

Рис. 4.11. Сигнально-точечное пространство модуляции для 16-ФМ

Отметим, что в отличие от ФМ сигналов сигналы КАМ, показанные на рис.4.12 не содержат постоянной огибающей. Наличие постоянной огибающей в ФМ объясняется поддержанием отношения уровней в квадратурных каналах. В КАМ такие ограничения не вводятся ввиду того, что в каждом канале уровни независимы. Отсюда следует, что КАМ не может использоваться с усилителями, которые могут иметь насыщения в пределах возможных мощностей.

Рис. 4.12. Схема модулятора- демодулятора КАМ

Спектр системы с КАМ определяется спектром исходных сигналов, поступающих в квадратурные каналы. Поскольку эти сигналы в своей основе имеют ту же структуру, что и исходные ФМ сигналы, спектр 16-КАМ и 64- ФМ совпадают при равном числе сигнальных точек на фазовой диаграмме.

Хотя спектры ФМ и КАМ совпадают, характеристики ошибок этих систем сильно отличаются. При достаточно большом числе сигнальных точек системы КАМ имеют, как правило, лучшие характеристики, чем системы с ФМ. Основная причина состоит в том, что расстояние между сигнальными точками на диаграмме для системы с КАМ больше, чем для соответствующей системы с ФМ. На рис.4.13 произведено сравнение систем 16-ФМ и 16-КАМ, работающих на одинаковой пиковой мощности, по расстоянию между точками.

Рис. 4.13. Сигнально-точечное пространство модуляции для 16-ФМ

Расстояние между соседними точками в системе КАМ с нормированной к единице пиковой амплитудой и числом уровней L может быть представлено в виде:

( 4.7)

n-КАМ имеет преимущество над системой n-ФМ при той же пиковой мощности.

В настоящее время для передачи пользуются системами 256- КАМ. Надо отметить, что надежное функционирование высокоплотных форматов модуляции, таких как 256-КАМ требует строгой линейности усилителей, для возможности обработки широкого диапазона амплитуд сигналов. Соотношения для характеристик ошибок методов 4-,16-,64- и 256 - КАМ в зависимости от отношения функции 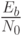приведены на рис.4.14

Рис. 4.14. Вероятности ошибки в системах с КАМ