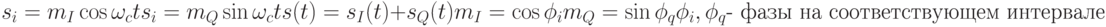Цифровая модуляция

Реализация модулятора

Возможные методы многоуровневой модуляции следующие:

1. Синтез требуемой формы сигнала с использованием цифровой обработки.
2. Формирование множества сигналов основанных на применении одной несущей, но имеющих разные фазы, и выбор сигнала в зависимости от значения данных.
3. Использование контролируемых задержек несущей.
4. Генерация сигналов, как линейной комбинации квадратурных сигналов.

Из этих методов наибольшее распространение получил последний –четвертый, так реализация сдвигов фаз или непосредственное вычисление синусоидального сигнала на основании формулы (4.1) сложно реализуема.

Прямая модуляция исходного многоуровнего сигнала возможна, если использовать так называемое, квадратурное представление сигнала.

Это представление основано на разложении синусоидального колебания в виде линейной комбинации косинусоидального и синусоидального колебания с нулевыми начальными фазами, которое определяется известным тригонометрическим тождеством.

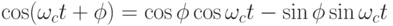
В этой формуле 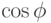и постоянны в пределах тактового интервала и представляют коэффициенты в линейной комбинации и с нулевой начальной фазой. Разность фаз между сигналами и составляет , поэтому они ортогональны на фазовой диаграмме, и тогда говорят, что сигналы находятся "в квадратуре".

В сущности, и представляют собой базисные векторы в двумерном пространстве фазовой диаграммы. Косинусоидальный сигнал часто называют синфазным или I – сигналом, а синусоидальный- сдвинутым по фазе или Q- сигналом.

В табл.4.1 приведен пример значения квадратурных коэффициентов (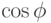 и ) при переменных и для квадратурного представления сигнала 4-ФМ.

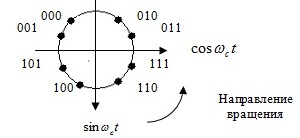
В табл.4.2 дано соответствующее представление для системы 8-ФМ и фазами сигналов, изображенными на рис. 4.3 . В фазовых диаграммах предполагается обход по часовой стрелке, и, следовательно, косинусоидальное колебание опережает синусоидальное на

Рис. 4.3. Фазовая диаграмма для сигнала 8 - ФМ

Таблица 4.1. Коэффициенты при квадратурном представлении сигнала XE "квадратурном представлении сигнала" для модуляции 4-ФМ

Значение данных	Квадратурные коэффициенты при		Составной сигнал
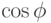01	0,707	- 0,707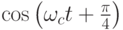
00	- 0,707	- 0,707
10	- 0,707	0,707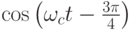
11	0,707	0,707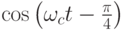

Таблица 4.2. Коэффициенты при квадратурном представлении сигнала XE "квадратурном представлении сигнала" для модуляции 8-ФМ

Значение данных	Квадратурные коэффициенты при		Составной сигнал
011	0,924	- 0,383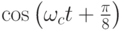
010	0,383	- 0,924
000	- 0,383	- 0,924
001	- 0,924	- 0,383
101	- 0,924	0,383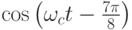
100	- 0,383	0,924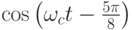
110	0,383	0,924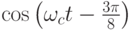
111	0,924	0,383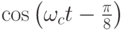

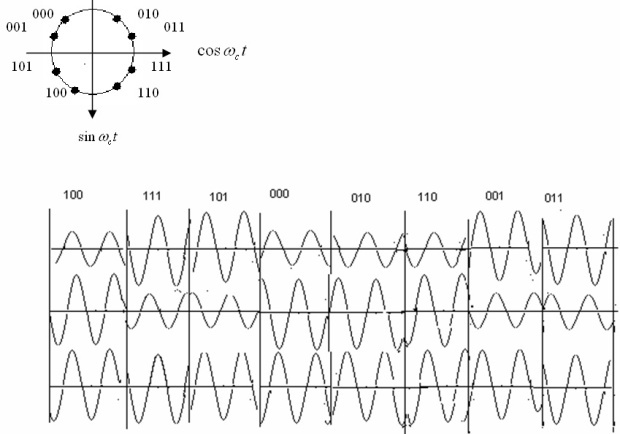
С помощью квадратурного представления возможна прямая модуляция Для этого необходимы два многоуровневых модулирующих сигнала: синфазный (I) и со сдвигом фазы (Q).Они обозначаются, как 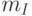и 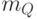соответственно. Уровни этих двух сигналов подбираются так, чтобы соответствовали коэффициентам необходимым для предоставления ФМ сигнала в виде линейной комбинации сигналов I и Q. В качестве примера на рис.4.4 показано, каким образом сигнал 8-ФМ, может быть получен сложением двух амплитудно-модулированных квадратурных сигналов.

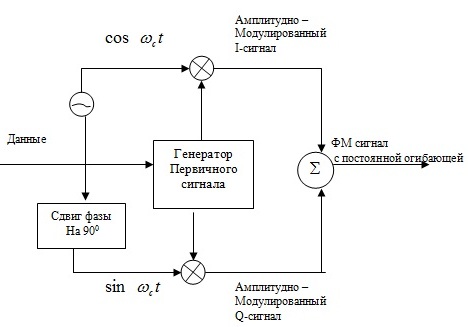
Обобщенная схема модулятора ФМ показана на рис.4.5 . Подобная форма модулятора выбрана как иллюстрация важных концепций модуляции, и она может быть полезна при анализе требований к спектру ФМ сигналов.

Рис. 4.4. Получение сигнала 8-ФМ, сложением двух амплитудно-модулированных квадратурных сигналов

Рис. 4.5. Обобщенная схема модулятора с ФМ