Методы автоматизированного проектирования конструкции и технологического процесса различного уровня иерархии
12.3. Функциональные и структурные модели
Основные признаки классификации и типы ММ, применяемые в САПР, приведены в следующей таблице 12.1 [38]:
| Признак классификации | Математические модели |
|---|---|
| Характер отображаемых свойств объекта | Структурные, функциональные |
| Принадлежность к иерархическому уровню | Микроуровень, макроуровень, метауровень |
| Степень детализации описания внутри одного уровня | Полные, макромодели |
| Способ представления свойств объекта | Аналитические, алгоритмические, имитационные |
| Способ получения | Теоретические, эмпирические |
По характеру отображаемых свойств объекта ММ делятся на структурные и функциональные.
Структурные ММ предназначены для отображения структурных свойств объекта. В свою очередь, структурные ММ делятся на топологические и геометрические.
Описание математических соотношений на уровнях структурных, логических и количественных свойств принимает конкретные формы в условиях определенного объекта.
Функциональные ММ предназначены для отображения физических или информационных процессов, протекающих в технологических системах при их функционировании.
Обычно функциональные ММ представляются системой уравнений, описывающих фазовые переменные, внутренние, внешние и выходные параметры.
В проектных процедурах, связанных с функциональным аспектом проектирования, как правило, используются ММ, отражающие закономерности процессов функционирования объектов, т.е. функциональные модели. Типичная функциональная модель представляет собой систему уравнений, описывающих либо электрические, тепловые, механические процессы, либо процессы преобразования информации.
В то же время в процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование математических моделей, отражающих только структурные свойства объекта, например его геометрическую форму, размеры, взаимное расположение элементов в пространстве, т. е. структурные модели. Структурные модели чаще всего представляются в виде графов, матриц инциденций и смежности, списков и т. п. [38].
Как правило, функциональные модели более сложные, поскольку в них отражаются также сведения о структуре объектов. Однако при решении многих задач конструирования использование сложных функциональных моделей неоправданно, так как нужные результаты могут быть получены на основе более простых структурных моделей. Функциональные модели применяют преимущественно на завершающих этапах верификации описаний объектов, предварительно синтезированных с помощью структурных моделей.
Проектирование технологического процесса изготовления изделия также характеризуется различными иерархическими уровнями: самый высокий уровень — разработка принципиальной схемы технологического процесса, который включает отдельные этапы, причем этап может содержать несколько или одну операцию. В данном случае оператором будет являться этап технологического процесса. Моделирование технологических процессов разного уровня происходит с помощью различных моделей и алгоритмов.
Иерархические уровни ММ делятся на микроуровни, макроуровни и метауровни. Особенностью ММ на микроуровне является отображение физических процессов в непрерывном пространстве и времени. С помощью дифференциальных уравнений в частных производных рассчитываются поля механических напряжений и деформаций.
На макроуровне используют укрупненную дискретизацию пространства по функциональному признаку, что приводит к представлению ММ на этом уровне в виде обыкновенных дифференциальных уравнений. В этих моделях имеются две группы переменных — независимых (время) и зависимых (фазовых). ММ на метауровне описывают укрупненно рассматриваемые объекты (технологические системы и т. п.). В качестве математического аппарата используют обыкновенные дифференциальные уравнения, теорию массового обслуживания, элементы дискретной математики (сети Петри и т. д.).
Теоретические модели строят на основании изучения закономерностей. В отличие от формальных моделей (например, эмпирических) они в большинстве случаев более универсальны и справедливы для широких диапазонов изменения технологических параметров. Теоретические модели могут быть линейными и нелинейными, а в зависимости от мощности множества значений переменных модели делят на непрерывные и дискретные. При технологическом проектировании наиболее распространены дискретные модели, переменные которых представляют собой дискретные величины, а множество решений — счетно. Различают также модели динамические и статические. В большинстве случаев проектирования технологических процессов используют статические модели, уравнения которых не учитывают инерционность процессов в объекте.
В полной ММ учитываются связи всех элементов проектируемого объекта, например маршрутная технология. Макро-ММ отображают значительно меньшее число межэлементных связей. Аналитические ММ представляют собой функциональные модели (теоретические или эмпирические) и, как правило, используются при параметрической оптимизации технологических процессов. Алгоритмическая ММ представляется в виде алгоритма. Имитационная модель является алгоритмической, отражающей поведение исследуемого объекта во времени при заданных внешних воздействиях на объект (например, процесс подготовки управляющих программ для роботизированной сборки).
Выбор типа математического моделирования, наиболее эффективного в условиях конкретной задачи, определяется его технологической сущностью, формой представления исходной технологической информации, общей целью исследования. Функциональная ММ может быть представлена в общем виде:
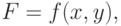 |
( 12.3) |
Ограничения, входящие в модель, имеют вид
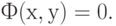 |
( 12.4) |
В зависимости от сложности задачи используются различные принципы построения моделей. Зачастую возникает необходимость разработки менее точной модели, но тем не менее более полезной для практики.
Возникают две задачи: с одной стороны, нужно разработать модель, на которой проще всего получить численное решение, а с другой — обеспечить максимально возможную точность модели. С целью упрощения модели используются такие приемы, как исключение переменных, изменение характера переменных, изменение функциональных соотношений между переменными (например, линейная аппроксимация), изменение ограничений (их модификация, постепенный ввод ограничений в условие задачи). Модели, являясь эффективным средством при исследовании структуры задачи, позволяют обнаружить принципиально новые стратегии.
12.4. Методика получения математических моделей элементов
Получение математических моделей элементов включает в себя следующие операции:
- Выбор свойств объекта, которые подлежат отражению в модели. Выбор основан на анализе возможных применений модели и определяет степень универсальности ММ.
- Сбор исходной информации о выбранных свойствах объекта. Источниками сведений могут быть: опыт и знания инженера, разрабатывающего модель; научно-техническая литература, прежде всего справочная; описания прототипов — имеющихся ММ для элементов, близких по своим свойствам к исследуемому объекту; результаты экспериментального измерения параметров и т. п.
- Синтез структуры ММ. Структура ММ — общий вид математических соотношений модели без конкретизации числовых значений фигурирующих в них параметров. Структура модели может быть представлена также в графической форме, например в виде эквивалентной схемы или графа. Синтез структуры — наиболее ответственная и наиболее трудно поддающаяся формализации операция.
- Расчет числовых значений параметров ММ. Эта задача ставится как задача минимизации погрешности модели заданной структуры.
- Оценка точности и адекватности ММ. Для оценки точности должны использоваться значения, которые не фигурировали при решении задачи.
Реализация функциональных ММ на ЭВМ подразумевает выбор численного метода решения уравнений и преобразование уравнений в соответствии с особенностями выбранного метода. Конечная цель преобразований — получение рабочей программы анализа в виде последовательности элементарных действий (арифметических и логических операций), реализуемых командами ЭВМ. Указанные преобразования исходной ММ в последовательности элементарных действий ЭВМ выполняет автоматически по специальным программам, создаваемым инженером — разработчиком САПР. Инженер-пользователь САПР должен лишь указать, какие программы из имеющихся он хочет использовать. Процесс преобразований ММ, относящихся к различным иерархическим уровням, иллюстрирует рис. 12.1.
Инженер-пользователь задает исходную информацию об анализируемом объекте и о проектных процедурах, подлежащих выполнению, на удобном для него проблемно-ориентированном языке программного комплекса. Ветви 1 на рис. 12.1 соответствует постановка задачи, относящейся к микроуровню, как краевой, чаще всего в виде ДУЧП. Численные методы решения ДУЧП основаны на дискретизации переменных и алгебраизации задачи.
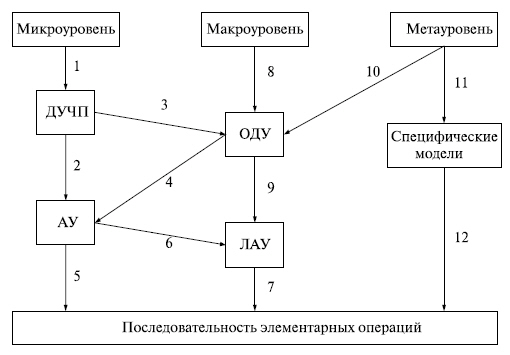
Рис. 12.1. Процесс преобразования ММ. ДУЧП — дифференциальные уравнения с частными производными; ОДУ — обыкновенные дифференциальные уравнения; АУ — алгебраические уравнения; ЛАУ — линейные алгебраические уравнения; 1...12 — взаимно направленные пути дискретизации переменных в ММ
Дискретизация заключается в замене непрерывных переменных конечным множеством их значений в заданных для исследования пространственном и временном интервалах; алгебраизация — в замене производных алгебраическими соотношениями.
Контрольные вопросы и упражнения
- Какую роль выполняют математические модели в проектировании РЭС?
- В чем суть блочно-иерархического подхода к проектированию?
- Поясните основные уровни проектирования РЭС. Приведите примеры.
- Как вводится функционально-логический уровень?
- Что называется стратой (аспектом описания)?
- Что называется математической моделью?
- Какие требования предъявляются к математическим моделям?
- Что называют адекватностью математической модели?
- Что называют областью адекватности ММ?
- Что называют структурными ММ? Приведите примеры.
- Что называют функциональной ММ? Приведите примеры.
- На какие части делятся структурные модели?
- Какие ММ используются для описания технологических процессов?
- Чем определяется выбор ММ?
- Изложите методику получения ММ элементов.
