Математические модели объектов проектирования РЭС
14.1. Общие сведения о математических моделях РЭС
Проектирование радиоэлектронных средств с применением ЭВМ требует описания этого объекта на языке математики в виде, удобном для его алгоритмической реализации.
Математическое описание проектируемого объекта называют математической моделью. Математическая модель — это совокупность математических элементов (чисел, переменных, векторов, множеств) и отношений между ними, которые с требуемой для проектирования точностью описывают свойства проектируемого объекта. На каждом этапе проектирования используется свое математическое описание проектируемого объекта, сложность которого должна быть согласована с возможностями анализа на ЭВМ, что приводит к необходимости иметь для одного объекта несколько моделей различного уровня сложности [38, 33, 55, 94].
В общей теории математического моделирования математическую модель любого объекта характеризуют внутренними, внешними, выходными параметрами и фазовыми переменными. Внутренние параметры модели определяются характеристиками компонентов, входящих в проектируемый объект, например номиналы элементов принципиальной схемы. Если проектируемый объект содержит п элементарных компонентов, то и его математическая модель будет определяться параметрами, которые образуют вектор внутренних параметров W = |w1...wn|T. Каждый из параметров wi, в свою очередь, может быть функцией, вектором или еще более сложным математическим функционалом в зависимости от объекта проектирования.
Выходные параметры модели — это показатели, характеризующие функциональные, эксплуатационные, конструкторско-технологические, экономические и другие характеристики проектируемого объекта. К таким показателям могут относиться коэффициенты передачи, масса и габариты проектируемого объекта, надежность, стоимость и т.п. Понятия внутренних и выходных параметров инвариантны, при моделировании на более сложном уровне выходные параметры могут стать внутренними и наоборот. Например, сопротивление резистора является внутренним параметром при моделировании усилительного устройства, компонентом которого он является, но это же сопротивление будет выходным параметром при моделировании самого резистора, что требуется при пленочном его исполнении. Вектор выходных параметров модели будем обозначать
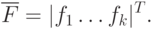
Внешние параметры модели — это характеристики внешней по отношению к проектируемому объекту среды, а также рабочие управляющие воздействия. Вектор внешних параметров в общем случае содержит множество самых различных составляющих. К его составляющим с полным правом можно отнести все, что говорилось ранее о составляющих вектора внутренних параметров. Будем обозначать его
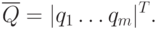
Уравнения математической модели могут связывать некоторые физические характеристики компонентов, которые полностью характеризуют состояние объекта, но не являются выходными или внутренними параметрами модели (например, токи и напряжения в радиоэлектронных устройствах, внутренними параметрами которых являются номиналы элементов электрических схем, а выходными параметрами — выходная мощность, коэффициент передачи). Такие характеристики называют фазовыми переменными. Минимальный по размерности вектор фазовых переменных v = |v1...vr|T, полностью характеризующий работу объекта проектирования, называют базисным вектором. Например, при составлении уравнений математической модели радиоэлектронных устройств в качестве базисного вектора V можно использовать вектор узловых потенциалов либо вектор напряжений на конденсаторах и токов в индуктивностях — переменные состояния. Использование вектора фазовых переменных позволяет упростить алгоритмическую реализацию программ, составляющих уравнения математической модели устройства.
В общем случае выходные параметры F представляются операторами от векторов V,W,Q и могут быть определены из решения системы уравнений математической модели устройства. С учетом вышесказанного математическая модель любого радиотехнического объекта может быть представлена в виде следующих систем уравнений:
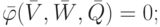 |
( 14.1) |
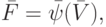 |
( 14.2) |
где 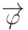 и
и 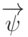 — операторы, определяющие вид систем уравнений модели.
— операторы, определяющие вид систем уравнений модели.
Система уравнений (14.1) может представлять собой систему линейных алгебраических уравнений, нелинейных уравнений различного вида, дифференциальных в полных или частных производных, и является собственно математической моделью проектируемого объекта. В результате решения системы (14.1) определяются действующие в устройстве фазовые переменные V. Система уравнений (14.2) определяет зависимость выходных параметров объекта от фазовых переменных V.
В частных случаях составляющие вектора V могут являться внутренними или выходными параметрами объекта, и тогда системы уравнений (14.1) и (14.2) упрощаются.
Часто моделированием называют лишь составление системы (14.1). Решение уравнений (14.1) и отыскание вектора F с помощью уравнения (14.2) называют анализом математической модели.
На каждом уровне моделирования различают математические модели проектируемого радиотехнического объекта и компонентов, из которых состоит объект. Математические модели компонентов представляют собой системы уравнений, которые устанавливают связь между фазовыми переменными, внутренними и внешними параметрами, относящимися к данному компоненту. Эти уравнения называют компонентными, а соответствующую модель — компонентной.
Математическую модель объекта проектирования, представляющего объединение компонентов, получают на основе математических моделей компонентов, входящих в объект. Объединение компонентных уравнений в математическую модель объекта осуществляется на основе фундаментальных физических законов, выражающих условия непрерывности и равновесия фазовых переменных, например законов Кирхгофа. Уравнения, описывающие эти законы, называют топологическими ; они отражают связи между компонентами в устройстве. Совокупность компонентных и топологических уравнений для проектируемого объекта и образует систему (14.1), являющуюся математической моделью объекта.
Исходя из задач конкретного этапа проектирования, математическая модель проектируемого объекта должна отвечать самым различным требованиям:
- отражать с требуемой точностью зависимость выходных параметров объекта от его внутренних и внешних параметров в широком диапазоне их изменения;
- иметь однозначное соответствие физическим процессам в объекте;
- включать необходимые аппроксимации и упрощения, которые позволяют реализовать ее программно на ЭВМ с различными возможностями;
- иметь большую универсальность, т. е. быть применимой к моделированию многочисленной группы однотипных устройств;
- быть экономичной с точки зрения затрат машинных ресурсов и т. п.
Эти требования в своем большинстве являются противоречивыми, и удачное компромиссное удовлетворение этих требований в одних задачах может оказаться далеким от оптимальности в других. По этой причине для одного и того же компонента или устройства часто приходится иметь не одну, а несколько моделей. В связи с этим классификация моделей должна выполняться по множеству признаков, чтобы описать все возможные случаи.
По уровню сложности различают полные модели и макромодели. Полные модели объекта проектирования получаются путем непосредственного объединения компонентных моделей в общую систему уравнений. Макромодели представляют собой упрощенные математические модели, аппроксимирующие полные.
В свою очередь, макромодели делят на две группы: факторные и фазовые модели.
Факторные модели предназначены для использования на последующих этапах проектирования.
Фазовые макромодели предназначены для использования на том же этапе проектирования, на котором их получают, для сокращения размерности решаемой задачи.
По способу получения математические модели радиотехнических объектов делят на физические и формальные. Физические модели получают на основе изучения физических закономерностей функционирования проектируемого объекта, так что структура уравнений и параметры модели имеют ясное физическое толкование.
Формальные модели получают на основе измерения и установления связи между основными параметрами объекта в тех случаях, когда физика работы его известна недостаточно полно. Как правило, формальные модели требуют большого числа измерений и по своей природе являются локальными, справедливыми вблизи тех режимов, в которых производились измерения. Такие модели называют моделями "черного ящика".
В современных системах автоматизированного проектирования формирование системы уравнений математической модели проектируемого объекта выполняется автоматически с помощью ЭВМ. В зависимости от того, что положено в основу алгоритма формирования системы уравнений, модели радиоэлектронных объектов можно разделить на электрические, физико-топологические и технологические.
Понятие электрической модели включает либо систему уравнений, связывающих напряжения и токи в электрической схеме, являющейся моделью объекта, либо саму электрическую схему, составленную из базовых элементов (резисторов, конденсаторов), на основе которой можно в ЭВМ получить систему уравнений, связывающих напряжения и токи в модели объекта.
В физико-топологических моделях исходными параметрами являются геометрические размеры определяющих областей проектируемого объекта и электрофизические характеристики материала, из которых они состоят. В результате решения системы уравнений этой модели поля находятся внутри и на внешних выводах устройства. Такие модели применяются при разработке полупроводниковых приборов, СВЧ-устройств и в ряде других случаев.
Технологические модели основываются на параметрах технологических процессов изготовления проектируемого объекта (температура и время диффузии, концентрация диффузанта). Выходные параметры такой модели — совокупность физико-топологических либо технологических параметров.
По способу задания внутренних и внешних параметров математические модели делят на дискретные и непрерывные.
Различают модели статические и динамические в зависимости от того, учитывают ли уравнения модели инерционности процессов в проектируемом объекте или нет. Статические модели отражают состояние объекта проектирования при неизменных внешних параметрах и не учитывают его переходные характеристики. Динамические модели дополнительно отражают переходные процессы в объекте, происходящие при изменении во времени внешних параметров.
Существуют и другие варианты классификации математических моделей элементов и узлов радиоустройств.
Программа моделирования радиотехнических и других объектов должна автоматически формировать систему уравнений математической модели из базового набора элементарных схемных элементов, компонентные уравнения для которых хранятся в библиотеке программы. Для синтеза адекватных реальному объекту моделей большинства радиотехнических устройств базовый набор должен содержать по крайней мере пять типов сосредоточенных схемных элементов, перечисленных в таблице 14.1. В таблице приведены и компонентные уравнения для каждого из элементов базового набора.
