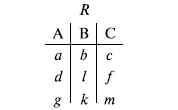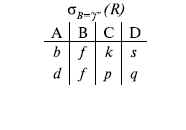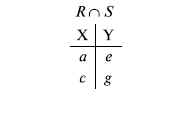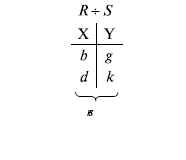Информационное обеспечение САПР (окончание)
11.1. Реляционная модель баз данных
Реляционная база данных, разработанная Э.Ф. Коддом (Е. F. Codd) в 1970 г., – это конечный набор конечных отношений (таблиц) вида рис. 10.3,б. Над отношениями можно осуществлять различные алгебраические операции. Тем самым теория реляционных баз данных становится областью приложения математической логики и современной алгебры и опирается на точный математический формализм.
Каждое отношение имеет свое имя; столбцы отношения соответствуют тому или иному атрибуту, имеющему имя и значения. Элементы отношения, соответствующие одной строке, составляют кортеж отношения ( рис. 10.3, б). Арность кортежа – число значений атрибутов в кортеже, т.е. число атрибутов в отношении [7,13, 31].
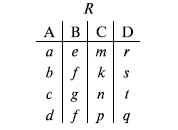
Схема отношения – список имен атрибутов вместе с именем отношения; так, для рис. 10.3,а схема отношения – ТРАНЗИСТОРЫ ( p, Iк max, Pк, Cк ), для рис. 10.3, б – ИМЯ ОТНОШЕНИЯ ( A, B, С, D ).
Домен – множество значений атрибутов (в том числе и только одного атрибута – один столбец). Вообще столбцы не обязательно являются поименованными, а порядок следования элементов в кортежах также несущественен.
Существует три подхода к анализу реляционных БД и формированию запросов в них: реляционная алгебра, реляционное исчисление на переменных-кортежах и реляционное исчисление на переменных- доменах.
В реляционных базах данных основные операции – включение, удаление, модификация и запрос данных – применяются к кортежам и доменам.
Для осуществления операции включения данных задаются новый кортеж и отношение, в которое он должен быть включен. Тогда значения нового кортежа образуют ключ файла включения данных.
При удалении данных должны быть заданы отношение и значения атрибутов, образующих ключ удаляемых кортежей.
При модификации данных задаются отношение, значения атрибутов ключа и новые значения для применяемых атрибутов. Преобразуются ключевые значения в значения полей. К файлу применяется процедура модификации.
Запрос в реляционных базах данных может быть сформулирован к одному или нескольким отношениям (таблицам). Например имеется запрос: указать типы всех транзисторов и их Pк, для которых Ск > 15 пФ. Тогда значение атрибута Ск = 15 пФ. Затем на печать выдается новый файл-отношение 
. Могут быть более сложные запросы: например, определить мощности рассеивания транзисторов, для которых 
, Iк max > 2а, Ск < 150 пФ и т. д. Тогда эти значения составляют ключ, и по ним составляется новое отношение Рк.
Все эти запросы реализуются с помощью специальных языков манипулирования данными, ряд из которых основан на реляционной алгебре.
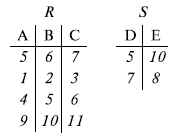
Основные операции реляционной алгебры приведены в табл. 11.1. В ней даны исходные отношения, результаты операций, а также в ряде случаев теоретико-множественное представление операций. Первые пять операций являются основными, остальные – дополнительные, которые могут быть выражены через пять основных.
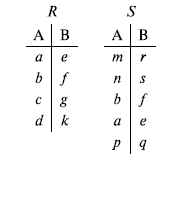
Объединение отношений 
– это множество кортежей (отношений), принадлежащих отношениям R, S или им обоим; отношения R и S должны иметь одинаковую арность.
Разность отношений R – S – множество кортежей, принадлежащих R, но не принадлежащих S. Отношения R и S также должны иметь одинаковую арность.
Декартово произведение отношений R x S – одна из основных операций по затратам машинного времени при формировании запросов к реляционной БД. При умножении отношений к каждому кортежу первого отношения ( R ) присоединяется каждый кортеж второго отношения ( S ) – конкатенация кортежей; при этом отношения R и S могут иметь одинаковую или различную арность. При декартовом умножении арности исходных отношений складываются, а количества кортежей – перемножаются.
Проекция отношения ![R[\pi _{X,Y} (R)]](/sites/default/files/tex_cache/b71dd33777df2a8d4022759d6e6aa96b.png)
– операции выборки по столбцам (атрибутам), приведенным в обозначении проекции.
Например, 
— отношение, составленное из атрибутов С и А отношения 
— отношение, составленное из 2-го и 3-го атрибутов отношения R, при этом арность проекции равна числу имен в ее обозначении.
Селекция отношения ![R [\sigma _{F} (R)]](/sites/default/files/tex_cache/f434d3ea46018ca9a1b203786c6abe8a.png)
— операция выборки по строкам (кортежам), удовлетворяющим формуле F. В формулу входят операнды, являющиеся константами или номерами (именами) атрибутов, арифметические операторы сравнения: 
и логические операторы 
.
Например, 
обозначает множество кортежей, в которых компоненты атрибута В равны f, или 
обозначает множество кортежей, в которых компоненты 2-го атрибута больше компонентов 3-го атрибута и одновременно равны компоненты атрибутов А и D ).
Пересечение отношений 
есть краткая запись для отношения R – (R – S) и обозначает множество кортежей, принадлежащих одновременно R и S.
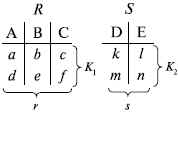
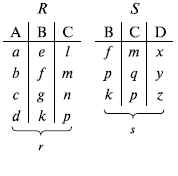
Частное отношений 
— множество кортежей, содержащих r – s первых компонентов кортежей отношения R, в которых остальные (s) компонентов принадлежат отношению S.
Соединение ( 
-соединение) отношений 
— это селекция (с формулой ) декартова произведения отношений R и S:
В частности, 
означает, что сначала надо выполнить декартово произведение отношений R и S, а затем в новом отношении выполнить селекцию по формуле А < D.
Эквисоединение отношений 
— это -соединение, если в формуле используются только равенства (см. таблицу 11.1, строку 9).
Естественное соединение 
— это эквисоединение, которое выполняется для атрибутов отношений R и S с одинаковыми именами (см таблицу 11.1, строку 10). Так как для указанных атрибутов имена и значения полностью совпадают, то один из них в каждой паре в результирующем отношении устраняют. Естественное соединение — одна из основных операций при формировании запросов к реляционной БД.
Композиция отношений — это проекция -соединения или проекции селекции декартова произведения. По сути, естественное соединение — тоже частный случай композиции. Декомпозиция отношений — это операция, обратная композиции, т. е. восстановление двух отношений из одного, естественное соединение которых образует исходное отношение.
В терминах реляционной алгебры легко записываются запросы к реляционной базе данных. Если задано несколько отношений, то запрос выражается в виде операции композиции к этим отношениям. Однако формальное применение композиции — последовательное применение декартова произведения всех отношений, селекции и проекции — приводит к неоправданным затратам машинного времени. Поскольку арность и число кортежей в исходных отношениях могут быть велики (десятки, сотни), нецелесообразно формировать сначала все декартово произведение, а только затем применять селекцию и проекцию. Так, если два отношения имеют по n кортежей и время доступа к каждой записи — t0, то общее время доступа к памяти для формирования полного декартова произведения Tдоступа = n2t0. Если n = 104, t0 = 10 мс, то Tдоступа = 106 11,5 сут. Поэтому с
- выполнять селекции и проекции как можно раньше до декартова умножения (с целью сокращения арности и количества кортежей);
- собирать в каскады селекции и проекции, чтобы выполнять их за один просмотр файла;
- обрабатывать (сортировать, индексировать) файлы перед выполнением соединения;
- комбинировать проекции с предшествующими или последующими двуместными операциями.
Для осуществления этой стратегии применяются эквивалентные выражения реляционной алгебры, приведенные в табл. 11.2. Законы коммутативности и ассоциативности означают произвольный выбор в очередности соединений и умножений. При перестановках проекции или селекции с декартовым произведением следует обращать внимание на принадлежность тех или иных имен атрибутов к исходным отношениям.
