Структуры данных и алгоритмы

Длиной списка называется число его элементов.

Первый аргумент h терма cons(h, t) обозначает элемент - голову списка, второй аргумент t обозначает список, который является хвостом исходного списка. Пустой список обозначается nil.

В данной лекции не будут использоваться встроенные операции над списками, которые имеются в языке Wolfram. Все операции над списками, представленными в виде описанных выше термов, моделируются в виде функций, которые определяются с помощью правил вида Elhs := rhs.

Определим следующие операции над списками: возвращение головы и хвоста списка, вычисление длины списка, возвращение элемента по индексу и индекса элемента, вставка элемента и соединение списков.

Пусть Z - множество, которому принадлежат элементы списка, и L - множество списков с элементами из Z. Операции возвращения головы списка и его хвоста определяются в виде функций head: L -> Z и tail: L -> L следующим образом:

head(cons(h, t)) = h;
tail(cons(h, t)) = t,

где . Областью определения обеих функций является множество непустых списков.

Пример 1. Пусть x = cons(1, cons(2, cons(3, nil))). Тогда

head(x) = 1; 
tail(x) = cons(2, cons(3, nil)).

На языке Wolfram определение этих операций имеет вид:

In[3]:=head[cons[h_, _]] := h
tail[cons[_, t_]] := t
head[x]
tail[x]
 Out[5]=1
 Out[6]= cons[2, cons[3, nil]]

Пусть 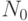- множество неотрицательных целых чисел.

Функцию вычисления длины списка можно определить с помощью следующего рекурсивного правила: длина пустого списка равна 0, а длина непустого списка на единицу больше длины его хвоста. Определение функции len имеет вид:

len(nil) = 0;
len(cons(h, t)) = 1 + len(t),

где . Но практическая реализация функции len в декларативных языках программирования приводит к большому расходу памяти. Поэтому для определения операции вычисления длины списка обычно используют две функции - основную функцию length: и вспомогательную . Они определяются следующим образом:

length(p) = auxlength(p, 0);
auxlength(nil, n) = n; 
auxlength(cons(h, t), n) = auxlength(t, n + 1),

где . Реализация таких функций в декларативных языках соответствует итерации в императивных языках.

Пример 2. Для списка x = cons(1, cons(2, cons(3, nil))) имеем:

length(x) = auxlength(x, 0) = auxlength(cons(2, cons(3, nil)), 1) = = auxlength(cons(3, nil), 2) = auxlength(nil, 3) = 3.

На языке Wolfram код выглядит следующим образом:

In[7]:=len[nil] := 0 
len[cons[_, t_]] := 1 + len[t] 
len[x]
 Out[9]= 3

 In[10]:= length[p_] := auxlength[p, 0]
auxlength[nil, n_] := n
auxlength[cons[_, t_], n_] := auxlength[t, n + 1]
length[x]
 Out[13]= 3

В дальнейшем для определения операций над структурами данных с помощью правил будет сразу использоваться код на языке Wolfram.

Функцию возвращения элемента по индексу nth можно определить следующим образом:

In[14]:= nth[cons[h_, _], 0] := h
nth[cons[_, t_], n_] := nth[t, n - 1]
nth[x, 2]
 Out[16]= 3

Если элемента в списке не существует, то возвращается выражение:

In[17]:= {nth[x, 4], nth[x, -1]}
 Out[17]= {nth[nil, 1], nth[nil, -4]} 

Для определения функции index возвращения индекса элемента в списке используем вспомогательную функцию auxind:

In[18]:= index[p_, a_] := auxind[p, a, 0]
auxind[cons[h_, _], h_, n_] := n
auxind[cons[_, t_], a_, n_] := auxind[t, a, n + 1]
index[x, 3]
index[x, 5]
 Out[21]= 2
 Out[22]= auxind[nil, 5, 3] 

Следующие две функции соответствуют операциям вставки элемента в список на заданную позицию n. Функция setnth заменяет элемент списка с индексом n новым элементом, функция insert "сдвигает" последующие элементы:

In[23]:= setnth[cons[_, t_], a_, 0] := cons[a, t]
setnth[cons[h_,t_],a_,n_]:=cons[h,setnth[t,a,n-1]]
setnth[x, 5, 2]
 Out[25]= cons[1, cons[2, cons[5, nil]]]

 In[26]:= insert[p_, a_, 0] := cons[a, p]
insert[cons[h_,t_],a_,n_]:=cons[h,insert[t,a,n-1]]
insert[x, 5, 2]
 Out[28]= cons[1, cons[2, cons[5, cons[3, nil]]]] 

Определение данных функций отличается первым правилом: если элемент вставляется на позицию 0, то он становится головой нового списка, а его хвостом в первом случае становится хвост старого списка, а во втором случае - сам исходный список.

Наконец, определим операцию соединения двух списков. Соединением пустого списка со вторым списком является второй список. Соединением непустого списка со вторым списком является список, голова которого совпадает с головой первого списка, а хвост является соединением хвоста первого списка со вторым списком.

Определение функции append соединения списков имеет вид:

In[29]:= 	append[nil, p_] := p
append[cons[h_, p_], q_] := cons[h, append[p, q]]
y = cons[3, cons[6, cons[5, cons[4, nil]]]];
append[x, y]
 Out[32]= cons[1, cons[2, cons[3, cons[3, cons[6, cons[5, cons[4, nil]]]]]]] 

Стек

Стек (англ. stack) - это тип данных, в котором элементы организованы по принципу "последний вошел - первый вышел" (англ. LIFO - last in - first out). В нем имеются операции добавления верхнего элемента в стек, возвращения верхнего элемента стека и удаления верхнего элемента из стека.

Иллюстрацией стека является стопка тарелок ( рис. 6.3), на которую можно положить еще одну тарелку или можно убрать верхнюю тарелку; посмотреть можно также только на верхнюю тарелку.

Рис. 6.3. Стопка тарелок как иллюстрация стека

Если стек имеет вид [1, 2, 3], то в результате добавления в него элемента 5 получится стек [1, 2, 3, 5]. Если удалить из него верхний элемент, т. е. элемент 5, то опять получится стек [1, 2, 3].

Ниже определяются функция push добавления элемента в стек, функция top, которая возвращает верхний элемент стека, и функция pop возращения стека без верхнего элемента:

In[33]:= push[nil, a_] := cons[a, nil]
push[cons[h_, t_], a_] := cons[h, push[t, a]]
push[x, 5]
 Out[35]= cons[1, cons[2, cons[3, cons[5, nil]]]]

 In[36]:= top[cons[h_, nil]] := h
top[cons[_, t_]] := top[t]
top[x]
 Out[38]= 3

 In[39]:= pop[cons[_, nil]] := nil
pop[cons[h_, t_]] := cons[h, pop[t]]
pop[x]
 Out[41]= cons[1, cons[2, nil]]