Нейронные сети и ...

Нейронные сети и статистическая физика

Данная тема заслуживает не одной книги и ей действительно посвящена обширнейшая литература. В настоящем курсе лекций мы не можем хоть сколько-нибудь подробно остановится на ней. Рассмотрим кратко лишь применение соответствующих идей к анализу сети Хопфилда. Демонстрация тесной аналогии, существующей между спиновыми стеклами и нейронными сетями, определила массированное и плодотворное вторжение методов статистической физики в теорию нейронных сетей в начале восьмидесятых годов. Сеть Хопфилда со стохастическими нейронами и явилась главной моделью, в которой применение этих методов оказалось наиболее значительным. Это чрезвычайно плодотворное обобщение модели, в некотором смысле эквивалентное переходу к сетям с градуальными нейронами. В нем нейроны являются стохастическими элементами и это обстоятельство открывает путь использованию методов статистической физики для анализа свойств ассоциативной памяти.

Стохастические нейроны

Стохастический нейрон, как и в оригинальной модели Хопфилда, является бинарным - его состояние принимает значения . Однако то, в какое состояние перейдет нейрон, связано со значением потенциала не однозначно, а случайным образом. Именно, вероятность перехода нейрона в состояния: , , , 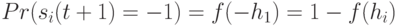или иначе

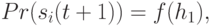
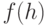где - распределение Ферми: , удовлетворяющее необходимым условиям 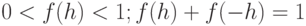, и - обратная температура. В низкотемпературном пределе распределение Ферми переходит в пороговую функцию, и поведение сети из стохастических нейронов становится аналогичным поведению сети Хопфилда, составленной из обычных бинарных нейронов.

Приближение среднего поля

Поскольку динамика состояний стохастических нейронов является вероятностной, можно интересоваться только средней активностью, или же ожидаемыми значениями их состояний

В силу нелинейности функции Ферми усреднение ее затруднительно, но в приближении среднего поля можно получить следующую замкнутую систему уравнений.

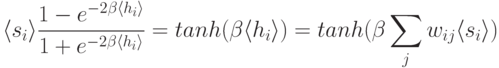
Фазовые переходы

На простом примере можно убедиться, что свойства сети критическим образом зависят от температуры 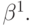Действительно, если величины всех синаптических связей положительны и равны между собой: (такая система эквивалентна ферромагнетику), то все уравнения системы сводятся к одному

Решение этого уравнения зависит от крутизны наклона функции гиперболического тангенса в начале координат (см. рисунок 11.5). При высокой температуре 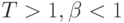уравнение имеет только тривиальное решение . Это означает, что состояния всех нейронов беспорядочно флуктуируют, принимая с равной вероятностью значения .

Однако, при снижении температуры ниже точки Кюри 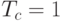в системе происходит фазовый переход, при котором тривиальное решение становится неустойчивым, а у уравнения среднего поля появляется еще два устойчивых нетривиальных решения .

Такое поведение характерно и для общего случая. Мы увидим далее, что в модели Хопфилда свойства ассоциативного запоминания и вызова образов проявляются в некоторой области температуры и дополнительного параметра - степени загрузки памяти. Вне этой области система переходит в неупорядоченное состояние.

Сеть Хопфилда с Хеббовскими связями

Рассмотрим интересующий нас случай сети, в которой связи вычислены по Хеббовскому правилу, исходя из вида запоминаемых векторов. В этом случае уравнения среднего поля принимают вид

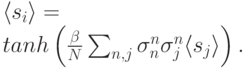
Если сеть работает как ассоциативная память, то разумно предположить, что каждому запоминаемому вектору 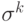должно соответствовать некоторое решение системы, совпадающего с ним с точностью до постоянного множителя

Подставляя это выражение в уравнения среднего поля и используя предположение, что все векторы памяти не коррелированы и значения их компонент с равной вероятностью принимают значения, получим:

В пределе 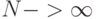, получаем знакомое уравнение для множителя m:

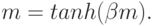
Вновь при высокой температуре 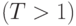это уравнение имеет только тривиальное решение и усредненная по времени конфигурация состояний нейронов не имеет ничего общего с запоминаемыми образами. При 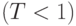уравнение имеет два решения , для которых средняя конфигурация активностей указывает на одно из запоминаемых состояний 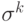, или на его "зеркального двойника" - 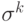. Из этих состояний однозначно восстанавливаются образы памяти. Однако, если сделать моментальный снимок состояния сети, то в силу флуктуаций она практически никогда не находится ни в одном из состояний памяти, всегда воспроизводя их с некоторой ошибкой. Теоретически было показано, что загрузка памяти, 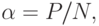оказывает на поведение системы такое же влияние, как температурный параметр в распределении Ферми. Когда этот параметр мал, каждому из запоминаемых некоррелированных образов соответствует стационарное состояние сети. Однако, при приближении его к критической емкости 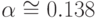, сеть внезапно теряет все свойства памяти. В плоскости координат области памяти и неупорядоченного поведения сети разделены границей, при пересечении которой происходит соответствующий фазовый переход. Более детальный анализ выявляет на фазовой диаграмме следующие 4 области: парамагнитную (P) фазу, в которой любой порядок разрушается высокой температурой; фазу спинового стекла (SG), в которой состояние сети не может эволюционировать к запомненным образам; смешанную (F+SG) - в ней запомненные образы метастабильны; и ферромагнитную (F) - в ней всем запоминаемым образам соответствуют глобальные минимумы энергии.

Наличие тепловых флуктуаций снижает вероятность попадания сети в состояние ложных минимумов. Критическая температура, при которых множество таких минимумов становится неустойчивыми, равна . Таким образом тепловой шум улучшает свойства памяти и наиболее благоприятным температурным интервалом работы сети является 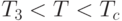.