Извлечение знаний с помощью нейронных сетей
Понимание закономерностей временных последовательностей
Исправление данных является важной компонентой подхода, позволяющего извлекать из нейронных сетей знания, касающиеся воспроизводимых ими временных закономерностей. Если, например, нейронная сеть обучена и используется для предсказания курса рубля по отношению к доллару, то естественно попытаться осмыслить связь большего или меньшего падения этого курса с теми или иными параметрами, подаваемыми на вход нейронной сети.
Кравен и Шавлик (Craven & Shavlik, 1996) разработали алгоритм TREPAN, порождающий дерево решений, аппроксимирующее поведение обученной нейронной сети. Важным достоинством алгоритма является то, что он не предъявляет никаких требований к архитектуре сети, числу ее элементов и связей (вспомним как важно было упростить структуру сети при использовании правила NeuroRule). Для него вполне достаточно того, что нейронная сеть является черным ящиком или Оракулом, которому можно задавать вопросы и получать от него ответы. Точность предсказания, даваемое сгенерированным деревом решений, близка к точности нейросетевого предсказания.
Приведем формальную схему алгоритма TREPAN Исходные данные обученная нейронная сеть (Оракул); обучающая выборка - S; множество признаков - F, min_sample - минимальное множество вопросов для каждого узла дерева, baem_width - число ветвей.
Инициализируем корень дерева R в виде листа. <Выборка векторов признаков> Используем все обучающее множество примеров S для конструирования модели распределения входных векторов, достигающих узла R.

 множество из
множество из  примеров, генерируемых моделью
примеров, генерируемых моделью 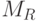 . <Используем нейронную сеть для классификации всех векторов признаков>
Для каждого вектора признаков
. <Используем нейронную сеть для классификации всех векторов признаков>
Для каждого вектора признаков  узнаем у Оракула принадлежность
узнаем у Оракула принадлежность  тому или иному классу - ставим метку класса
тому или иному классу - ставим метку класса 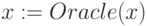 <Осуществляем наилучшее первое расширение дерева>
Инициализируем очередь
<Осуществляем наилучшее первое расширение дерева>
Инициализируем очередь  , составленную из наборов
, составленную из наборов  До тех пор пока очередь
До тех пор пока очередь  не пуста и глобальный критерий остановки не выполнен <создаем узел в начале очереди>
удаляем
не пуста и глобальный критерий остановки не выполнен <создаем узел в начале очереди>
удаляем  из начала очереди
из начала очереди  .
Используем
.
Используем  и beam_width для конструирования в узле
и beam_width для конструирования в узле  разветвления
разветвления  . lt;создаем узлы следующего поколения>
Для каждого ответвления t разветвления
. lt;создаем узлы следующего поколения>
Для каждого ответвления t разветвления  создаем
создаем  - новый дочерний узел
- новый дочерний узел 

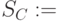 члены
члены 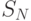 с ответвлением t.
Конструируем модель
с ответвлением t.
Конструируем модель  распределения примеров, покрываемых узлом
распределения примеров, покрываемых узлом 

 множество из
множество из  примеров, сгенерированных моделью
примеров, сгенерированных моделью  и ограничением
и ограничением  Для каждого вектора признаков
Для каждого вектора признаков 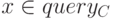 ставим метку класса
ставим метку класса 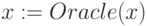 <временно принимаем, что узел С является листом>
Используем
<временно принимаем, что узел С является листом>
Используем 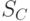 и
и  для определения метки класса для С. <Определяем должен ли узел С расширяться>
если локальный критерий остановки не удовлетворен то
поместить <
для определения метки класса для С. <Определяем должен ли узел С расширяться>
если локальный критерий остановки не удовлетворен то
поместить <  > в очередь
> в очередь  .
Вернуть дерево с корнем
.
Вернуть дерево с корнем  .
.TREPAN поддерживает очередь листьев, которые раскрываются и порождают поддеревья. В каждом узле очереди TREPAN сохраняет: (i) подмножество примеров, (ii) еще одно множество векторов, который называется набором вопросов (query) и (iii) набор ограничений ( ). Подмножество примеров включает просто те векторы обучающего набора, которые достигают данного узла дерева. Дополнительный набор вопросов Оракулу используется для выбора теста на разветвление в узле и определения класса примеров, если узел является листом. Алгоритм всегда требует, чтобы число примеров, на основе которых оценивается узел, было бы не меньше заданного (min_sample). Если же до данного узла доходит меньшее число примеров, TREPAN генерирует новые искусственные примеры, используя набор ограничений в данном узле. Множество ограничений определяет условия, которым должны удовлетворять примеры, чтобы достичь данного узла - эта информация используется при формировании набора вопросов для создаваемого нового узла. Для завершения процедуры построения дерева TREPAN использует локальный критерий - он оценивает состояние данного узла и решает, превратить ли его в лист, и глобальные критерии - максимальный размер дерева и общую оценку качества классификации примеров деревом.
Возникает естественный вопрос: "А зачем вообще нужна нейронная сеть для данного алгоритма?" Ведь он может просто использовать
обучающую выборку - известно же, какому классу принадлежит каждый пример. Более того, как бы хорошо ни была обучена сеть, она все
равно будет делать ошибки, неправильно классифицируя некоторые примеры. Дело в том, что именно использование нейросетей в качестве
Оракула дает возможность получать деревья решений, имеющих более простую структуру, чем у деревьев, обученных на исходных примерах.
Это является следствием как хорошего обобщения информации нейронными сетями, так и использования при их обучении операции
исправления данных ( CLEARNING ). Кроме того, алгоритмы построения деревьев, исходя из тренировочного набора данных, действительно
разработаны и с их помощью такие деревья строятся путем рекурсивного разбиения пространства признаков. Каждый внутренний узел
подобных деревьев представляет критерий расщепления некоторой части этого пространства, а каждый лист дерева - соответствует
классу векторов признаков. Но в отличие от них TREPAN конструирует дерево признаков методом первого наилучшего расширения.
При этом вводится понятие наилучшего узла, рост которого оказывает набольшее влияние на точность классификации генерируемым деревом.
Функция, оценивающая узел  , имеет вид
, имеет вид 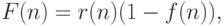 где
где 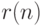 - вероятность достижения узла
- вероятность достижения узла  примером, а
примером, а 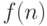 - оценка правильности обработки этих
примеров деревом. TREPAN очень интересно осуществляет разделение примеров, достигающих данный внутренний узел дерева, а именно,
использует так называемый
- оценка правильности обработки этих
примеров деревом. TREPAN очень интересно осуществляет разделение примеров, достигающих данный внутренний узел дерева, а именно,
использует так называемый  тест. Такой тест считается выполненным, когда выполняются по меньшей мере одно из условий. Если,
например, имеется 3 булевых переменных
тест. Такой тест считается выполненным, когда выполняются по меньшей мере одно из условий. Если,
например, имеется 3 булевых переменных 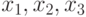 , то использование выражения
, то использование выражения  будет
эквивалентно использованию логической функции
будет
эквивалентно использованию логической функции 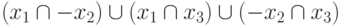 .
Подобная формулировка правил делает деревья вывода более компактными и четкими. Приведем пример дерева решений, полученного
алгоритмом TREPAN, Оракулом в которой являлась нейронная сеть, обученная предсказывать курс обмена немецкой марки на доллар
(Weigend et al., 1996). Заметим, что для обучения сети использовался рекомендуемый для финансовых приложений метод CLEARNING, с
которым мы уже познакомились. Сеть обучалась на данных, охватывающих период с 1985 по 1994 гг. и предсказывала рост или падение
курса обмена на следующий день в течение всего 1995 г.
.
Подобная формулировка правил делает деревья вывода более компактными и четкими. Приведем пример дерева решений, полученного
алгоритмом TREPAN, Оракулом в которой являлась нейронная сеть, обученная предсказывать курс обмена немецкой марки на доллар
(Weigend et al., 1996). Заметим, что для обучения сети использовался рекомендуемый для финансовых приложений метод CLEARNING, с
которым мы уже познакомились. Сеть обучалась на данных, охватывающих период с 1985 по 1994 гг. и предсказывала рост или падение
курса обмена на следующий день в течение всего 1995 г.
Таким образом, нейронные сети могут эффективно использоваться в практически важных задачах извлечения хорошо сформулированных знаний не только в случае, если их структура достаточно проста, но и в общем случае.
