Извлечение знаний с помощью нейронных сетей
Извлечение правил из нейронных сетей
Рассмотрим один из методов извлечения правил из нейронных сетей, обученных решению задачи классификации (Lu, Setiono and Liu, 1995).
Этот метод носит название NeuroRule.
Задача состоит в классификации некоторого набора данных с помощью многослойного персептрона и последующего анализа полученной сети с
целью нахождения классифицирующих правил, описывающих каждый из классов.
Пусть A обозначает набор из N свойств A1,A2...AN, а {a} - множество возможных значений, которое
может принимать свойство Ai. Обозначим через С множество классов c1,c2...cN. Для обучающей
выборки известны ассоциированные пары векторов входных и выходных значений (a1...am,ck), где ck 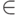 C.
Алгоритм извлечения классифицирующих правил включает три этапа:
C.
Алгоритм извлечения классифицирующих правил включает три этапа:
- Обучение нейронной сети. На этом первом шаге двухслойный персептрон тренируется на обучающем наборе вплоть до получения достаточной точности классификации.
- Прореживание (pruning) нейронной сети. Обученная нейронная сеть содержит все возможные связи между входными нейронами и нейронами скрытого слоя, а также между последними и выходными нейронами. Полное число этих связей обычно столь велико, что из анализа их значений невозможно извлечь обозримые для пользователя классифицирующие правила. Прореживание заключается в удалении излишних связей и нейронов, не приводящем к увеличению ошибки классификации сетью. Результирующая сеть обычно содержит немного нейронов и связей между ними и ее функционирование поддается исследованию.
-
Извлечение правил. На этом этапе из прореженной нейронной сети извлекаются правила, имеющие форму
если ( a1
 q1 ) и ( a2
q1 ) и ( a2  q2 ) и ... и ( an
q2 ) и ... и ( an  qn ), то cj, где qj -
константы,
qn ), то cj, где qj -
константы,  - оператор отношения (
- оператор отношения (  ). Предполагается, что эти правила
достаточно очевидны при проверке и легко применяются к большим базам данных.
). Предполагается, что эти правила
достаточно очевидны при проверке и легко применяются к большим базам данных.
Рассмотрим все эти шаги более подробно.
Обучение нейронной сети
Предположим, что обучающий набор данных необходимо расклассифицировать на два класса A и B. В этом случае сеть должна содержать N входных и 2 выходных нейрона. Каждому из классов будут соответствовать следующие активности выходных нейронов (1,0) и (0,1). Подходящее количество нейронов в промежуточном слое, вообще говоря, невозможно определить заранее - слишком большое их число ведет к переобучению, в то время как малое не обеспечивает достаточной точности обучения. Тем не менее, как уже отмечалось ранее, все методы адаптивного поиска числа нейронов в промежуточном слое делятся на два класса, в соответствии с тем, с малого или большого числа промежуточных нейронов стартует алгоритм. В первом случае по мере обучения в сеть добавляются дополнительные нейроны, в противоположном - после обучения происходит уничтожение излишних нейронов и связей. NeuroRule использует последний подход, так что число промежуточных нейронов выбирается достаточно большим. Заметим, что NeuroRule уничтожает также и избыточные входные нейроны, влияние которых на классификацию мало.
В качестве функции активации промежуточных нейронов используется гиперболический тангенс, так что их состояния изменяются в
интервале ![[-1,1]](/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) . В то же время, функцией активации выходных нейронов является функция Ферми (состояния в интервале
. В то же время, функцией активации выходных нейронов является функция Ферми (состояния в интервале ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) ).
Обозначим через
).
Обозначим через  - состояния выходных нейронов при предъявлении на вход сети вектора признаков
- состояния выходных нейронов при предъявлении на вход сети вектора признаков  -го объекта
-го объекта 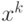 . Будем считать, что этот объект правильно классифицирован сетью, если
. Будем считать, что этот объект правильно классифицирован сетью, если
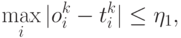
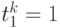 если
если  и
и  если
если  , а
, а  . В остальных случаях
. В остальных случаях 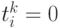 .
.Минимизируемая функция ошибки должна не только направлять процесс обучения в сторону правильной классификации всех объектов обучающей выборки, но и делать малыми значения многих связей в сети, чтобы облегчить процесс их прореживания. Подобную технологию - путем добавления к функции ошибки специально подобранных штрафных членов - мы уже разбирали в "Обучение с учителем: Распознавание образов" . В методе NeuroRule функция ошибка включает два слагаемых


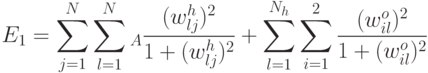
Здесь 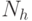 - число нейронов в скрытом слое,
- число нейронов в скрытом слое, 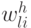 - величина связи, между
- величина связи, между  -м входным и
-м входным и  -м скрытым нейронами
-м скрытым нейронами 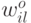 - вес связи между
- вес связи между  -м скрытым и
-м скрытым и  -м выходным нейронами.
-м выходным нейронами.
Использование регуляризирующего члена  приводит к дифференциации весов по величинам, уменьшая большинство, но сохраняя
значения некоторых из них. Обучение сети производится методом обратного распространения ошибки.
приводит к дифференциации весов по величинам, уменьшая большинство, но сохраняя
значения некоторых из них. Обучение сети производится методом обратного распространения ошибки.
Прореживание нейронной сети
Полное число связей в обученной сети составляет 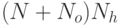 . Можно показать, что связь между входным и промежуточным
нейроном
. Можно показать, что связь между входным и промежуточным
нейроном 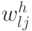 можно удалить без снижения точности классификации сетью при выполнении условий
можно удалить без снижения точности классификации сетью при выполнении условий  и
и  . Аналогичным образом, удаление связи
. Аналогичным образом, удаление связи 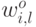 не влияет на качество классификации если
не влияет на качество классификации если 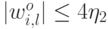 .
.
