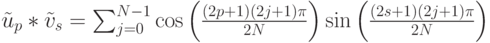НОУ ИНТУИТ | Квантовые вычисления. Лекция 16: Дискретное преобразование Фурье

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 03.06.2019 | Доступ: платный | Студентов: 55 / 14 | Длительность: 09:11:00

Темы: Программирование, Математика, Физика, Суперкомпьютерные технологии

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Преобразование Фурье - это математический инструмент для изучения периодических или почти периодических функций. Хорошим примером почти периодических функций является звуковая волна, порождаемая звучанием музыкального инструмента. Давайте рассмотрим простейшее музыкальное устройство - вибрирующую струну Если "щипнуть" натянутую струну, то она начнет вибрировать и ее колебания порождают колебания воздуха вокруг струны.

В результате возникает звуковая волна, периодически распространяющаяся область высокого давления воздуха, сменяющаяся областью низкого давления. Эти волны распространяются в пространстве, удаляясь от источника звука. Для записи звука используется микрофон, имеющий внутри гибкую мембрану Сразу же как звуковая волна достигает микрофона, область высокого давления заставляет мембрану сжиматься, а низкого давления - тянет мембрану в обратном направлении. Микрофон преобразует колебания мембраны в электрический сигнал, который следует движениям мембраны. В аналоговой записи звука электрический сигнал может использоваться для намагничивания ленты, так что интенсивность магнитного поля ленты воспроизводит профиль звукового сигнала. В цифровой записи звука электрический сигнал, создаваемый микрофоном, измеряется. Измерения, проводимые с заданным временным интервалом, могут сохраняться в памяти компьютера. Например, для системы записи СD (компакт дисков) измерения проводятся с частотой 44100 Герц, что означает запись 44100 измерений в секунду Величина сигнала обычно масштабируется в интервале от-1 до 1.

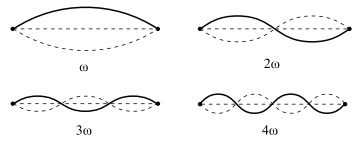
Давайте вернемся к обсуждению колеблющейся струны. Колеблющаяся струна издает звук с некоторой частотой, которая называется базовой частотой $\omega$ . Оказывается, что струна может колебаться более сложным способом. Она может иметь состояния высокой вибрации с частотой $2\omega,\; 3\omega,\; 4\omega$ и так далее. На практике, колебание струны включает колебания высокой вибрации в дополнение к колебаниям с базовой частотой. В музыке,

состояния высокой вибрации, производимые музыкальным инструментом, называются обертонами. Распределение интенсивности обертонов - это то, что отличает один инструмент от другого, играющего одну и ту же ноту.

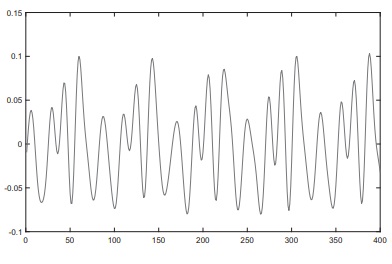
Ниже на рисунке представлена диаграмма звучания флейты, соответствующая примерно 0,01 секунды записи. Заметьте, что профиль почти периодический, - на диаграмме можно выделить 5 периодов.

Следующая диаграмма показывает спектр частот этой звуковой волны.

Поскольку это звук музыкального инструмента, играющего одну ноту, то диаграмма представляет пики, соответствующие базовой частоте (587 Нz; нота D второй октавы) и обертонам базовой частоты. Заметьте, для этого инструмента в частотном спектре отсутствует второй обертон.

Анализ частотного спектра сигнала, представленного выше, выполнен с использованием дискретного преобразования Фурье (ДПФ), которое мы намереваемся далее обсудить.

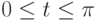Давайте рассмотрим функцию f(t) , определенную на интервале $0 \le t \le\pi$ . Мы хотим измерить f(t) в N равноудаленных точках 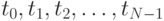$t_0, t_1, t_2, \dots, t_{N-1}$ с расстоянием между точками равным $\frac{\pi}{N}$ . Первую точку выберем не в 0, а в середине первого интервала - в точке $t_0=\frac{\pi}{2N}$ . Тогда $t_1=t_0+\frac{\pi}{N}=\frac{3\pi}{2N},\; t_2=t_1=\frac{\pi}{N}=\frac{5\pi}{2N}$ , и так далее с общей формулой:

$t_j=\frac{(2j+1)\pi}{2N}$

Последняя точка будет закрывать правый конец интервала:

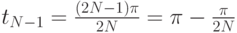
$t_{N-1}=\frac{(2N-1)\pi}{2N}=\pi-\frac{\pi}{2N}$

Измеряя f(t) в этих точках получим N-компонентный вектор

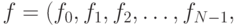
$f=(f_0, f_1, f_2, \dots, f_{N-1},$

где 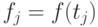f_j = f (t_j) .

Далее будем полагать, что N четно, N = 2М.

Волны будем моделировать периодическими функциями cos(t) и sin(t). С этого момента будем полагать, что аргументы тригонометрических функций измеряются в радианах. Давайте рассмотрим семейство функций:

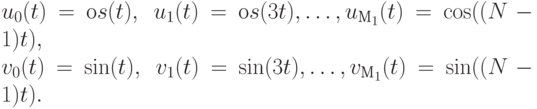
$u_0(t) = \соs(t),\; u_1(t) = \соs(3t), \dots , u_{М_1}(t) = \cos((N - 1)t),\\ v_0(t) = \sin(t),\; v_1(t) = \sin(3t), \dots , v_{М_1}(t) = \sin((N - 1)t).$

Мы можем записать их в более общей форме:

$u_р(t) = \cos((2р + 1)t),\; u_p(t) = \sin((2р + 1)t),\; р = 0,1, \dots ,М - 1.$

Используя измерения в ряде точек, можно перейти от непрерывных функций к их дискретным аналогам, создавая для каждой функции N-компонентный вектор:

$\tilde u_0=(\cos(t_0), \cos(t_1), \cos(t_2),\dots, \cos(t_{N-1)),\\ \tilde u_1=(\cos(3t_0), \cos(3t_1), \cos(3t_2),\dots, \cos(3t_{N-1)),\\ \tilde u_2=(\cos(5t_0), \cos(5t_1), \cos(5t_2),\dots, \cos(5t_{N-1)),$

Аналогично, выполним эти действия и для функции v_p(t) .

Подставляя значения для точек 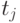t_j , получим:

$\tilde u_p=\left (\cos \left( \frac{(2p+1)\pi}{2N} \right), \cos \left (\frac{(2p+1)3\pi}{2N} \right ), \dots, \cos \left (\frac{(2p+1)(2N-1)\pi}{2N} \right ) \right)\\ \tilde v_p=\left (\sin \left( \frac{(2p+1)\pi}{2N} \right), \sin \left (\frac{(2p+1)3\pi}{2N} \right ), \dots, \sin \left (\frac{(2p+1)(2N-1)\pi}{2N} \right ) \right)$

Здесь р принимает значения р = 0,1,..., М - 1.

В результате мы получили семейство из N векторов в 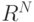R^N . Давайте изучим их свойства.

Теорема. Вектора $\{\tilde u_0, \tilde u_1, \dots, \tilde u_{M-1}, \tilde v_0, \tilde v_1, \dots, \tilde v_{M-1}/}$ ортогональны друг другу и формируют базис в R^N

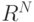
Прежде чем доказывать теорему, вспомним некоторые тригонометрические тождества.

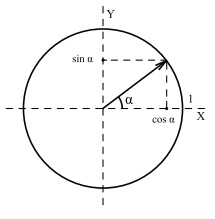
При рассмотрении свойств тригонометрических функций важно все время помнить, что 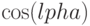$\cos(\аlpha)$ - это Х-координата точки единичного круга, соответствующая углу $\alpha$ , в то время как $\sin(\аlpha)$ - это Y-координата той же точки. Из этого определения непосредственно следуют следующие свойства:

$\cos(-\аlpha) = \соs \аlpha, \; \sin(-\alpha) = - \sin \аlpha.$

Только две тригонометрические формулы следует непосредственно держать в памяти:

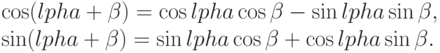
$\cos(\аlpha + \beta) = \cos \аlpha \cos \beta - \sin \аlpha \sin \beta,\\ \sin(\аlpha + \beta) = \sin \аlpha \cos \beta + \cos \аlpha \sin \beta.$

Все остальные тождества непосредственно выводимы. Изменяя знак $\beta$ в предыдущих формулах, получим:

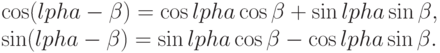
$\cos(\аlpha - \beta) = \cos \аlpha \cos \beta + \sin \аlpha \sin \beta,\\ \sin(\аlpha - \beta) = \sin \аlpha \cos \beta - \cos \аlpha \sin \beta.$

Комбинируя формулы, мы получим:

$\cos(\аlpha + \beta) + \cos(\аlpha - \beta) = 2 \cos \аlpha \cos \beta,\\ \cos(\аlpha - \beta)- \cos(\аlpha + \beta) = 2 \sin \аlpha \sin \beta,\\ \sin(\аlpha + \beta) + \sin(\аlpha -\beta) = 2 \sin \аlpha \cos \beta.$

Нам понадобится следующее

Утверждение. Предположим 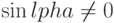$\sin \аlpha \ne 0$ . Тогда

$\cos(\аlpha) + \cos(3\аlpha) + \cos(5\аlpha) + \dots + \соs((2N - 1)\аlpha) =\frac{\sin(2N\alpha)}{2 \sin \аlpha},\\ \sin(\аlpha) + \sin(3\аlpha) + \sin(5\аlpha) + \dots + \sin((2N -1)\аlpha) =\frac{1 - \cos(2N\alpha)}{2 \sin \аlpha}$

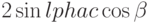
Для доказательства первого тождества нашего утверждения умножим его слева на $2 \sin \аlpha$ и применим формулу для $2 \sin \аlphac \cos \beta$

$2 \sin \аlpha \cos(\аlpha) + 2 \sin \аlpha \соs (3\аlpha) + 2 \sin \аlpha \cos (5\аlpha)+\dots + 2 \sin \alpha \cos((2N -1)\аlpha)\\ = (\sin(2\аlpha) - \sin(0)) + (\sin(4\аlpha) - \sin(2\аlpha)) + (\sin(6\аlpha) - \sin(4\аlpha))+\dots+ (\sin(2N\alpha)-\sin((2N-2)\аlpha)).$

Большинство слагаемых в формуле будут взаимно уничтожаться, останется только 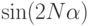$\sin(2N\alpha)$ . Разделив обе стороны на $2 \sin \аlpha$ , получим первое тождество.

Доказательство второго тождества остается в качестве упражнения.

Доказательство теоремы. Для доказательства нам нужно вычислить скалярное произведение векторов нашего семейства:

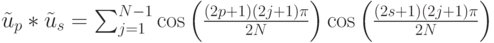
$\tilde u_p*\tilde u_s=\sum_{j=1}^{N-1}\cos \left (\frac{(2p+1)(2j+1)\pi}{2N}\right ) \cos\left ( \frac{(2s+1)(2j+1)\pi}{2N} \right )$

Применяя формулу для произведения косинусов, получим:

$\frac12\sum_{j=0}^{N-1}\cos \left ( \frac{(2p+2s+2)(2j+1)\pi}{2N} \right )+\cos \left ( \frac{(2p-2s)(2j+1)\pi}{2N} \right )$

Далее, используя предыдущее утверждение вычислим сумму:

$\frac12 \sum_{j=0}^{N-1}\cos\left ( \frac{(p+s+1)(2j+1)\pi}{N}\right) =\frac{\sin\left (\frac{(p+s+1)\pi}{N}\right )}{4\sin \left (\frac{(p+s+1)\pi}{N}\right )}$

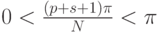Эти вычисления справедливы при условии, что синус в знаменателе не равен нулю. Это так, поскольку $0\le p,s \le M-1$ , откуда следует, что $0 <\frac{(p+s+1)\pi}{N} < \pi$ , следовательно, sin в знаменателе не равен нулю.

Вычисляя вторую сумму, получим:

$\frac 12 \sum_{j=0}^{N-1} \cos \left(\frac{(p-s)(2j+1)\pi}{N}\right )=\frac{\sin\left ( \frac{(p-s)2N\pi}{N}\right )}{4\sin\left (\frac{(p-s)\pi}{N}\right)}$

Эти вычисления также справедливы при условии, что синус в знаменателе не равен нулю. Здесь знаменатель превращается в ноль только тогда, когда р = s. Заметьте, что оба числителя в этом случае также равны нулю. Следовательно, когда $р \ne s$ скалярное произведение $\tilde u_p*\tilde v_s$ равно нулю. Если р = s, то первая сумма по-прежнему равна нулю, а во второй все косинусы равны 1, так что скалярное произведение векторов равно N/2. Давайте теперь вычислим скалярное произведение $\tilde u_p*\tilde v_s$

$\tilde u_p*\tilde v_s=\sum_{j=0}^{N-1}\cos \left(\frac{(2p+1)(2j+1)\pi}{2N}\right )\sin \left (\frac{(2s+1)(2j+1)\pi}{2N}\right )$

Дальше >>

Авторизоваться

Квантовые вычисления

Дискретное преобразование Фурье

Вопросы и ответы