Лекция 10: Арифметические операции над числами с плавающей запятой
Формат числа с плавающей запятой
Число с плавающей запятой представляется в виде мантиссы (М) и порядка (П).
Например, число А = 123 может быть представлено в виде числа с мантиссой 12,3 и порядком +1, то есть 12,3 *10+1. Другие представления этого самого же числа могут выглядеть так: 123 = 123*100 = 1230 10-1 = 0,123*10+3 = 0, 0123 * 10+4 = ...
Для того чтобы число с плавающей запятой представлялось единственным образом, его мантисса должна быть нормализована, то есть на нее накладывается следующее ограничение.
Нормализованная мантисса должна удовлетворять условию:
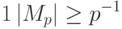 |
( 10.1) |
где р – основание системы счисления, то есть мантисса представляет собой правильную дробь, у модуля которой старшая цифра отлична от нуля.
Из приведенного выше примера этому условию удовлетворяет лишь запись
А = 0,123*10+3
Как мантисса, так и порядок могут быть как положительными, так и отрицательными числами. Поэтому в общем виде число с плавающей запятой имеет следующий формат (Рис. 10.1). В дальнейшем мы рассмотрим, как форма кодирования чисел в ЭВМ сказывается на этом формате. В этой лекции будем исходить именно из такой формы представления числа с плавающей запятой, так как она позволяет выявить все особенности обработки таких чисел.
Порядок представляет собой число с фиксированной точкой, мантисса – число с фиксированной запятой. Поэтому:
Ммакс = 0,1 ... 1 = 1-2-n
Ммин = 2-1 (напомним, что мантисса должна быть нормализована).
Пмакс = 0,1 ... 1 = 2m-1
-Пмакс = -(2m-1)
Мы пока ведем речь только о естественном, а не машинном представлении числа, где, например, в так называемом дополнительном коде можно представить на одну комбинацию отрицательных чисел больше, чем положительных.
В данном случае достаточно просто определить диапазон представляемых чисел
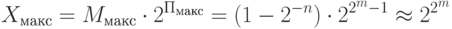

Абсолютная погрешность представления числа с плавающей запятой ЭВМ составит:

Относительная погрешность представления в ЭВМ числа с плавающей запятой будет равна:
![\delta \left[Х\right]_{мин} = \triangle\left[Х\right]/ (М_{макс}\cdot 2^{П{_x }})= (2^{-1} \cdot2^{-m})\cdot 2^{П{_x}} / ((1 - 2^{-m})\cdot 2^{П{_x }} ) \approx 2^{-1}\cdot 2^{-m}](/sites/default/files/tex_cache/fac8191969e4853662f5cefcebc2a387.png)
![\delta \left[Х\right]_{макс} = \triangle\left[Х\right]/ (М_{мин}\cdot 2^{П{_x }})= (2^{-1} \cdot2^{-m})\cdot 2^{П{_x}} / (2^{-1}\cdot 2^{П{_x }} ) = 2^{-m}](/sites/default/files/tex_cache/e10c98cac88d139066650bee20eae0a2.png)
Таким образом, мы видим, что для чисел с плавающей запятой диапазон их представления весьма широк и определяется в основном, количеством разрядов, отводимых под порядок числа, а относительная погрешность меняется гораздо меньше, чем для чисел с фиксированной точкой (всего в 2 раза) и определяется количеством разрядов, отводимых под запись мантиссы числа.
Умножение чисел с плавающей запятой
Сначала рассмотрим случай перемножения двух чисел с плавающей запятой в десятичной системе счисления.
(0,3*103) * (0,2*102) = (0,3 * 0,2) *103+2 = 0,06 * 105 = 0,6* 104
Последний шаг выполнен для нормализации мантиссы результата.
Таким образом, если представить операнды в двоичной системе счисления как
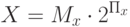
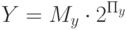
а произведение мы хотим тоже получить в виде числа с плавающей запятой, то есть
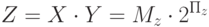
то умножение сводится к двум простейшим действиям, рассмотренным ранее: сложению порядков сомножителей как целых чисел и перемножению мантисс как операндов с фиксированной запятой. При необходимости к ним добавляется еще нормализация мантиссы результата:
Пz = Пx + Пy
Mz = Mx * My
Интерес здесь представляют особые случаи, которые могут возникнуть на различных этапах обработки числа. Так при сложении чисел с фиксированной точкой (речь идёт о порядках) может возникнуть переполнение, которое сделает невозможным дальнейшую работу с этим числом, либо при перемножении мантисс сомножителей мы получим денормализованную мантиссу результата, что потребует ее коррекции с одновременной коррекцией полученного ранее порядка произведения. Все эти и некоторые другие обстоятельства необходимо учитывать при проведении данной операции.
Ряд этих случаев будем рассмотрен нами при обсуждении ГОСТа IEEE 754 на представление чисел с плавающей запятой [ ...]. В то же время иногда подобные ситуации возникают в процессе выполнения самой операции, а окончательный результат оказывается допустимым числом. Рассмотрим все эти случаи.
Особые случаи при умножении чисел с плавающей запятой
Главное обстоятельство, на которое следует обратить внимание при умножении чисел с плавающей запятой, это диапазон мантисс, которые получаются при выполнении операции.
Так как мы исходим из того, что мантиссы обоих операндов нормализованы, то есть удовлетворяют условию
1 > |Mx,y| ? 2-1,
то 1 > |Mz| = |Mx| * |My| ? 2-2.
Таким образом, нормализация мантиссы если и потребуется, то только путем сдвига на один разряд влево. При этом порядок, естественно, следует уменьшить на 1. Отсюда вытекает следующая последовательность действий.
- Пz = Пx + Пy
- Если Пz = - ?, то Z=0 .
- Если Пz = + ?, то продолжить умножение, так как последующая операция над мантиссами может привести к коррекции порядка результата в сторону его уменьшения и, тем самым, обеспечит нормальное представление числа в целом.
- Mz = Mx * My
Т.к. |Mx| ? 2-1, |My| ? 2-1, то |Mz| ? 2-2
Возможная область ненормализованной мантиссы:
2-1 > |Mz| ? 2-2
Если |Mz| < 2-1, то выполнить нормализацию мантиссы с одновременной коррекцией порядка:
|Mz| = |Mz| * 2+1
Пz = Пz -1
Если в результате получим Пz = - ?, то Z=0.
Если в ходе перемножения мантисс получим |Mz| ? 2-1 , но ранее при обработке порядков получили Пz = + ? (см п.1.2), то Z = ?
При Z=0 выполнение программы в ЭВМ продолжается.
При Z = ? устанавливается флаг прерывания, и ЭВМ приостанавливает обработку данных чисел.

