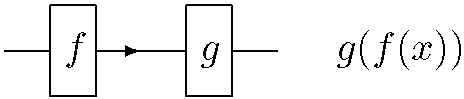
Схемы из функциональных элементов
Формулы представляют собой способ записи композиции функций.
Например, если мы сначала применяем функцию  , а потом
функцию
, а потом
функцию  , это можно записать формулой
, это можно записать формулой 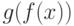 . Но
есть и другой способ: можно изобразить каждую функцию в виде
прямоугольника с "входом"и "выходом"и соединить
выход функции
. Но
есть и другой способ: можно изобразить каждую функцию в виде
прямоугольника с "входом"и "выходом"и соединить
выход функции  со входом функции
со входом функции  (рис. 2.1).
(рис. 2.1).
Такое представление отнюдь не является чисто теоретическим. В течении нескольких десятков лет электронная промышленность выпускает микросхемы, которые выполняют логические операции. Такая микросхема имеет электрические контакты, напряжение на которых кодирует логические значения И и Л. Конкретное напряжение зависит от типа схемы, но обычно это несколько вольт, и высокий потенциал (относительно заземления) считается единицей, а низкий нулем.
Одной из типичных схем является схема И-НЕ, она имеет два входа
и один выход. Сигнал на выходе является отрицанием конъюнкции
сигналов на входе. Другими словами, на выходе появляется высокий
потенциал (сигнал  ) тогда и только тогда, когда на одном из
входов потенциал низкий (
) тогда и только тогда, когда на одном из
входов потенциал низкий (  ). Из такой схемы легко получить
схему НЕ (изменяющую уровень сигнала на противоположный),
соединив проводом два входа. При этом на оба входа поступает
один и тот же сигнал, и операция И его не меняет (
). Из такой схемы легко получить
схему НЕ (изменяющую уровень сигнала на противоположный),
соединив проводом два входа. При этом на оба входа поступает
один и тот же сигнал, и операция И его не меняет ( 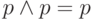 ),
а НЕ меняет на противоположный. Взяв два элемента И-НЕ и используя
второй из них в качестве элемента НЕ, инвертирующего сигнал с выхода
первого элемента, получаем схему, которая реализует функцию И. А
если поставить два элемента НЕ перед каждым из входов элемента
И-НЕ, получим схему, реализующую функцию ИЛИ:
),
а НЕ меняет на противоположный. Взяв два элемента И-НЕ и используя
второй из них в качестве элемента НЕ, инвертирующего сигнал с выхода
первого элемента, получаем схему, которая реализует функцию И. А
если поставить два элемента НЕ перед каждым из входов элемента
И-НЕ, получим схему, реализующую функцию ИЛИ: 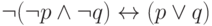 .
.
Теорема 3 о полноте системы связок теперь гарантирует, что любую булеву
функцию можно реализовать в виде схемы. Надо иметь в
виду, однако, что предлагаемая в ее доказательстве
конструкция (дизъюнктивная нормальная форма) имеет
скорее теоретический интерес, поскольку приводит к
схемам очень большого размера даже для простых
функций (если число аргументов велико). Например,
схема, сравнивающая два 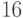 -битных числа, должна
иметь
-битных числа, должна
иметь 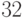 входа и поэтому в ее реализации с помощью
дизъюнктивной нормальной формы будет порядка
входа и поэтому в ее реализации с помощью
дизъюнктивной нормальной формы будет порядка  элементов — что мало реально. (Между тем такую схему
можно построить гораздо проще, из нескольких сотен элементов.)
элементов — что мало реально. (Между тем такую схему
можно построить гораздо проще, из нескольких сотен элементов.)
Поэтому вопрос о том, сколько элементов нужно для реализации той или иной функции, представляет большой интерес — как практический, так и философский. (Одна из центральных проблем математики и информатики, так называемая "проблема перебора", может быть сформулирована в этих терминах.)
Мы сейчас дадим более формальное определение схемы и реализуемой ей булевой функции. Но прежде всего ответим на такой вопрос — почему мы вообще говорим о схемах? Ведь можно записать композицию булевых функций в виде формулы, не будет ли это то же самое?
Оказывается, не совсем, и разницу легко увидеть на примере (рис. 2.2).
Здесь один и тот же элемент схемы (  ) приходится
указывать в формуле дважды, поскольку его выход
используется в качестве входа двух других
элементов. Схемы, в которых такого ветвления нет
(на практике ветвление вполне возможно, хотя и ограничено
"нагрузочной способностью выхода", как говорят
инженеры), как раз и соответствуют формулам. Но
в общем случае полученная из данной схемы
формула может быть длинной, даже
если схема содержит небольшое число элементов, поскольку
число копий может расти экспоненциально с ростом
глубины схемы.
) приходится
указывать в формуле дважды, поскольку его выход
используется в качестве входа двух других
элементов. Схемы, в которых такого ветвления нет
(на практике ветвление вполне возможно, хотя и ограничено
"нагрузочной способностью выхода", как говорят
инженеры), как раз и соответствуют формулам. Но
в общем случае полученная из данной схемы
формула может быть длинной, даже
если схема содержит небольшое число элементов, поскольку
число копий может расти экспоненциально с ростом
глубины схемы.
Хотя идея образования схемы из функциональных
элементов, реализующих булевы функции, достаточно
наглядна, дадим более формальное определение.
Фиксируем некоторый набор булевых функций  .
Пусть имеется
.
Пусть имеется  булевых (принимающих значения
булевых (принимающих значения  и
и  ) переменных
) переменных 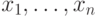 ,
называемых входами. Пусть также имеется некоторое число булевых
переменных
,
называемых входами. Пусть также имеется некоторое число булевых
переменных 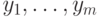 , называемых проводниками.
Пусть для каждого проводника схемы задана булева функция из
, называемых проводниками.
Пусть для каждого проводника схемы задана булева функция из  , выражающая его значение через другие проводники
и входы. При этом требуется, чтобы не было циклов
(цикл образуется, когда
, выражающая его значение через другие проводники
и входы. При этом требуется, чтобы не было циклов
(цикл образуется, когда  зависит от
зависит от 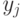 , которое зависит от
, которое зависит от  , которое зависит от
, которое зависит от  ). Пусть, кроме того,
среди проводников выделен один, называемый выходом.
В таком случае говорят, что задана
схема из функциональных элементов в базисе
). Пусть, кроме того,
среди проводников выделен один, называемый выходом.
В таком случае говорят, что задана
схема из функциональных элементов в базисе  с
с  входами. Число
входами. Число  называют размером схемы.
(С точки зрения инженера размер — это число использованных элементов, а базис
называют размером схемы.
(С точки зрения инженера размер — это число использованных элементов, а базис  — это ассортимент доступных ему элементов.)
— это ассортимент доступных ему элементов.)
Отсутствие циклов гарантирует, что есть проводник, зависящий только от входов (иначе можно было бы найти цикл: возьмем какой-то проводник, затем возьмем тот проводник, от которого он зависит и т. д.). Значение этого проводника, таким образом, однозначно определяется сигналами на входах. Среди оставшихся проводников также нет цикла, поэтому можно найти один из них, зависящий только от уже известных, и определить его значение. Перенумеровав проводники в таком порядке, мы можем записать последовательность присваиваний

 ,
примененные ко входам и уже найденным значениям. При
этом можно считать, что результат схемы есть
,
примененные ко входам и уже найденным значениям. При
этом можно считать, что результат схемы есть 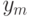 (все последующие присваивания уже не нужны).
Такая программа определяет
(все последующие присваивания уже не нужны).
Такая программа определяет 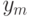 при известных
значениях входов, и тем самым вычисляет некоторую булеву функцию.
при известных
значениях входов, и тем самым вычисляет некоторую булеву функцию.Теперь набор булевых функций  можно назвать полным,
если любая булева функция может быть задана схемой из
можно назвать полным,
если любая булева функция может быть задана схемой из  -элементов (существует программа, ее
вычисляющая, при этом в правых частях присваиваний
стоят функции из
-элементов (существует программа, ее
вычисляющая, при этом в правых частях присваиваний
стоят функции из  ). Ясно, что это определение полноты
равносильно прежнему, то есть возможности записать булеву функцию в виде формулы со
связками из
). Ясно, что это определение полноты
равносильно прежнему, то есть возможности записать булеву функцию в виде формулы со
связками из  (как мы говорили, разница
только в том, что один и тот же элемент будет фигурировать в формуле многократно).
(как мы говорили, разница
только в том, что один и тот же элемент будет фигурировать в формуле многократно).
Сложностью булевой функции  относительно
относительно  называют минимальный размер схемы из
называют минимальный размер схемы из  -
элементов, вычисляющей функцию
-
элементов, вычисляющей функцию  . Его обозначают
. Его обозначают  .
.