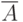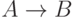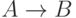Логика высказываний
Высказывания и операции
"Если число  рационально, то
рационально, то  —
алгебраическое число. Но оно не алгебраическое. Значит,
—
алгебраическое число. Но оно не алгебраическое. Значит,  не рационально."
Мы не обязаны знать, что такое число
не рационально."
Мы не обязаны знать, что такое число  , какие числа называют
рациональными и какие алгебраическими, чтобы признать, что это
рассуждение правильно — в том смысле, что из двух
сформулированных посылок действительно вытекает заключение.
Такого рода ситуации — когда некоторое утверждение верно
независимо от смысла входящих в него высказываний — составляют
предмет логики высказываний.
, какие числа называют
рациональными и какие алгебраическими, чтобы признать, что это
рассуждение правильно — в том смысле, что из двух
сформулированных посылок действительно вытекает заключение.
Такого рода ситуации — когда некоторое утверждение верно
независимо от смысла входящих в него высказываний — составляют
предмет логики высказываний.
Такое начало (особенно если учесть, что курс логики входил в программу философского факультета, где также изучалась "диалектическая логика") настораживает, но на самом деле наши рассмотрения будут иметь вполне точный математический характер, хотя мы начнем с неформальных мотивировок.
Высказывания могут быть истинными и ложными. Например, " 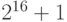 —
простое число "— истинное высказывание, а "
—
простое число "— истинное высказывание, а " 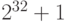 — простое число"—
ложное (это число делится на
— простое число"—
ложное (это число делится на 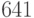 ). Про высказывание "
существует бесконечно много простых
). Про высказывание "
существует бесконечно много простых  , для которых
, для которых  — также простое "никто не берется сказать наверняка, истинно
оно или ложно. Заметим, что "
— также простое "никто не берется сказать наверняка, истинно
оно или ложно. Заметим, что "  делится на
делится на  " в
этом смысле не является высказыванием, пока не сказано, чему
равно
" в
этом смысле не является высказыванием, пока не сказано, чему
равно  ; при разных
; при разных  получаются разные
высказывания, одни истинные (при четном
получаются разные
высказывания, одни истинные (при четном  ), другие— ложные (при
нечетном
), другие— ложные (при
нечетном  ).
).
Высказывания можно соединять друг с другом с помощью "
логических связок". Эти связки имеют довольно странные, но
традиционные названия и обозначения (табл. 1.1).
Отметим также, что в импликации  высказывание
высказывание  называют посылкой, или антецедентом импликации,
а
называют посылкой, или антецедентом импликации,
а  — заключением, или консеквентом.
— заключением, или консеквентом.
| связка | обозначение | название |
|---|---|---|
 и и 
|
|
конъюнкция |
 или или 
|
|
дизъюнкция |
|
не
|
not |
отрицание |
|
из если
|
|
следование |
Говорят также, что высказывание имеет истинностное значение И (истина), если оно истинно, или Л (ложь),
если оно ложно. Иногда вместо И употребляется буква T
(true) или число  , а вместо Л — буква F
(false) или число
, а вместо Л — буква F
(false) или число  . (С первого взгляда идея произвольным
образом выбрать числа
. (С первого взгляда идея произвольным
образом выбрать числа  и
и  кажется дикой —
какая бы польза могла быть от, скажем, сложения истинностных значений?
Удивительным образом в последние годы обнаружилось, что такая польза есть,
и если оперировать с истиной и ложью как элементами конечного поля, можно получить
много неожиданных результатов. Но это выходит за рамки нашей книги.)
кажется дикой —
какая бы польза могла быть от, скажем, сложения истинностных значений?
Удивительным образом в последние годы обнаружилось, что такая польза есть,
и если оперировать с истиной и ложью как элементами конечного поля, можно получить
много неожиданных результатов. Но это выходит за рамки нашей книги.)
Логические связки позволяют составлять сложные высказывания из простых. При этом истинность составного высказывания определяется истинностью его частей в соответствии с таблицей 1.2.
Те же правила можно изложить словесно. Высказывание  истинно, если оба высказывания
истинно, если оба высказывания  и
и  истинны.
Высказывание
истинны.
Высказывание 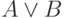 истинно, если хотя бы одно из высказываний
истинно, если хотя бы одно из высказываний  и
и  истинно. Высказывание
истинно. Высказывание 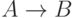 ложно
в единственном случае: если
ложно
в единственном случае: если  истинно, а
истинно, а  ложно.
Наконец,
ложно.
Наконец, 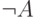 истинно в том и только том случае, когда
истинно в том и только том случае, когда  ложно.
ложно.
Из всех связок больше всего вопросов вызывает импликация. В
самом деле, не очень понятно, почему надо считать, скажем,
высказывания "если 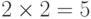 , то
, то 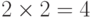 "и "если
"и "если 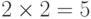 , то
, то 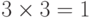 "
истинными. (Именно так говорят наши таблицы:
"
истинными. (Именно так говорят наши таблицы: 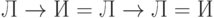 .)
Следующий пример показывает, что в таком определении есть смысл.
.)
Следующий пример показывает, что в таком определении есть смысл.
Общепризнано, что если число  делится на
делится на  , то
оно делится на
, то
оно делится на  . Это означает, что высказывание
. Это означает, что высказывание
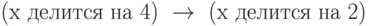
 . Подставим сюда
. Подставим сюда  : обе части
ложны, а утверждение в целом истинно. При
: обе части
ложны, а утверждение в целом истинно. При 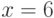 посылка импликации ложна, а
заключение истинно, и вся импликация истинна. Наконец, при
посылка импликации ложна, а
заключение истинно, и вся импликация истинна. Наконец, при 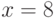 посылка и заключение истинны и импликация в целом истинна. С другой
стороны, обратное утверждение (если
посылка и заключение истинны и импликация в целом истинна. С другой
стороны, обратное утверждение (если  делится на
делится на  ,
то
,
то  делится на
делится на  ) неверно, и число
) неверно, и число  является
контрпримером. При этом посылка импликации истинна, заключение ложно, и сама
импликация ложна. Таким образом, если считать, что истинность
импликации определяется истинностью ее частей (а не наличием
между ними каких-то причинно-следственных связей), то все
строки таблицы истинности обоснованы. Чтобы подчеркнуть такое
узко-формальное понимание импликации, философски настроенные
логики называют ее "материальной импликацией".
является
контрпримером. При этом посылка импликации истинна, заключение ложно, и сама
импликация ложна. Таким образом, если считать, что истинность
импликации определяется истинностью ее частей (а не наличием
между ними каких-то причинно-следственных связей), то все
строки таблицы истинности обоснованы. Чтобы подчеркнуть такое
узко-формальное понимание импликации, философски настроенные
логики называют ее "материальной импликацией".Теперь от неформальных разговоров перейдем к определениям. Элементарные высказывания (из которых составляются более сложные) мы будем обозначать маленькими латинскими буквами и называть пропозициональными переменными. Из них строятся пропозициональные формулы по таким правилам:
- Всякая пропозициональная переменная есть формула.
- Если
 — пропозициональная формула, то
— пропозициональная формула, то 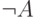 — пропозициональная формула.
— пропозициональная формула. - Если
 и
и  — пропозициональные формулы, то
— пропозициональные формулы, то  ,
, 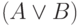 и
и  — пропозициональные формулы.
— пропозициональные формулы.
Можно еще сказать так: формулы образуют минимальное множество, обладающее указанными свойствами (слово "минимальное" здесь существенно: ведь если бы мы объявили любую последовательность переменных, скобок и связок формулой, то эти три свойства были бы тоже выполнены).
Пусть формула  содержит
содержит  пропозициональных
переменных
пропозициональных
переменных 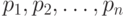 . Если подставить вместо этих
переменных истинностные значения ( И или Л ), то по таблицам
можно вычислить истинностное значение формулы в целом. Таким
образом, формула задает некоторую функцию от
. Если подставить вместо этих
переменных истинностные значения ( И или Л ), то по таблицам
можно вычислить истинностное значение формулы в целом. Таким
образом, формула задает некоторую функцию от  аргументов,
каждый из которых может принимать значения Л и И. Значения
функции также лежат в множестве
аргументов,
каждый из которых может принимать значения Л и И. Значения
функции также лежат в множестве 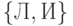 , которое мы будем
обозначать
, которое мы будем
обозначать 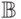 . Мы будем следовать уже упоминавшейся
традиции и отождествлять И с единицей, а Л — с нулем, тем
самым
. Мы будем следовать уже упоминавшейся
традиции и отождествлять И с единицей, а Л — с нулем, тем
самым 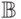 есть
есть  . Формула
. Формула  задает отображение типа
задает отображение типа  . Такие отображения называют
также булевыми функциями
. Такие отображения называют
также булевыми функциями  аргументов.
аргументов.