Оптимальные эксперименты с линейными автоматами
При исследовании различных видов экспериментов с автоматами в классической теории чаще всего рассматриваются задачи построения минимальных по длине входных последовательностей. Других критериев, кроме длины, для сравнения различных экспериментов в этой теории не используется. Это обстоятельство объясняется тем, что по умолчанию предполагаются равными затраты на подачу различных входных символов, из которых составлена соответствующая входная последовательность, подаваемая в процессе проведения эксперимента.
Вместе с тем упомянутые затраты в действительности могут быть различны, и при подаче двух последовательностей одинаковой длины, отличных по составу входных символов, суммарные затраты могут существенно отличаться. Это, в частности, происходит в том случае, когда моделью автомата описывается некоторый технологический процесс, включающий в качестве входных воздействий разного рода механические действия. Последние могут потребовать выполнения значительной работы, измеряемой, к примеру, в эргах, или затрат мощности, измеряемой в ваттах, и т. п.
В силу сказанного возникает проблема оптимального управления экспериментом по критериям минимизации общих затрат. Заметим, что некоторые эксперименты с автоматами, в частности, эксперименты по распознаванию состояний, можно рассматривать как процессы управления. Например, синхронизацию автомата можно трактовать как процесс управления автоматом путем подачи входной последовательности, устанавливающей автомат в известное заключительное состояние независимо от того, в каком начальном состоянии он находился.
В теории оптимального управления как непрерывными [38], [40], [41], так и дискретными системами [14] [42], входные воздействия, обеспечивающие достижения цели управления, оцениваются по различным содержательным критериям.
Вообще говоря, подобного рода критерии могут быть использованы и при построении теории экспериментов с автоматами.
Хотя линейный автомат и является дискретной системой, однако его задание над конечным полем 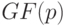 исключает возможность использования результатов упомянутой теории оптимального управления, поскольку последняя развита для случая вещественного и комплексного полей.
исключает возможность использования результатов упомянутой теории оптимального управления, поскольку последняя развита для случая вещественного и комплексного полей.
Оптимальные синхронизирующие эксперименты
В этом разделе рассматриваются ЛА, фазовые пространства которых состоят из обобщенных состояний (ОС), определенных в
"Обобщенные автоматы без потери информации"
. Условимся считать, что в вектор-столбце, представляющем ОС, неопределенными являются последние  его координат.
его координат.
Напомним, что ЛА, для которого существует обобщенная синхронизирующая последовательность (ОСП), называется обобщенно синхронизируемым. Состояние, в котором рассматриваемый ЛА оказывается после подачи ОСП, называется обобщенным синхросостоянием.
Поскольку перевод ЛА в одно и то же обобщенное синхросостояние может осуществляться несколькими ОСП, то введем критерий, по которому будем сравнивать различные ОСП.
Каждому входному символу 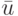 ЛА поставим в соответствие действительное число
ЛА поставим в соответствие действительное число 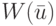 , называемое весом символа. Весом входной последовательности
, называемое весом символа. Весом входной последовательности 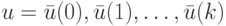 назовем величину
назовем величину

Содержательно вес входной последовательности  можно интерпретировать как суммарные затраты на ее подачу.
можно интерпретировать как суммарные затраты на ее подачу.
Рассмотрим следующую задачу. Пусть задан обобщенно синхронизируемый ЛА и некоторые обобщенное синхросостояние  . Требуется найти ОСП минимального веса, переводящую ЛА из произвольного начального состояния в ОС
. Требуется найти ОСП минимального веса, переводящую ЛА из произвольного начального состояния в ОС  . При этом предполагается, что множество допустимых начальных состояний ЛА совпадает со всем множеством его состояний.
. При этом предполагается, что множество допустимых начальных состояний ЛА совпадает со всем множеством его состояний.
Прежде чем перейти к решению этой задачи, исследуем некоторые свойства множества всех синхросостояний ЛА и его ОСП.
Условимся ОСП наименьшей длины для ЛА называть далее минимальной ОСП и обозначать ее длину через  .
.
Теорема 18.1. Если ЛА является обобщенно синхронизируемым, то для любого  множество синхросостояний, порождаемых всеми ОСП длины
множество синхросостояний, порождаемых всеми ОСП длины  , совпадает с множеством синхросостояний, порождаемых всеми ОСП длины
, совпадает с множеством синхросостояний, порождаемых всеми ОСП длины  .
.
Доказательство. Предположим, что ОСП  длины
длины  переводит ЛА в обобщенное синхросостояние
переводит ЛА в обобщенное синхросостояние  . Это означает, что
. Это означает, что
![[A^k}_{\mu}\bar s(0)+[A^{k-1}]_{\mu}\bar u(0)+ \dots +[B]_{\mu}\bar u(k-1)=[\bar s]_{\mu}](/sites/default/files/tex_cache/0fb74c76eb9edd4ada52f757b9e2326b.png) |
( 18.1) |
Поскольку  есть ОСП, то по теореме 1.18
есть ОСП, то по теореме 1.18 ![[A^k]_{\mu}=[0]](/sites/default/files/tex_cache/ed06628d567d48e19352af74d795017d.png) и тогда (18.1) примет вид
и тогда (18.1) примет вид
![[A^{k-1}B]_{\mu}\bar u(0)+\dots + [B]_{\mu}\bar u(k-1)=[\bar s]_{\mu}](/sites/default/files/tex_cache/736d9e8396998ef747d46a201725b2e0.png) |
( 18.2) |
или
![Q(k)u=[\bar s]_{\mu}](/sites/default/files/tex_cache/7384ab7e8edafab01fbdc449f5f17813.png) |
( 18.2) |
где
![Q(k)=[A^{k-1}B, \dots, B]_{\mu}, u=[\bar u(0), \dots, \bar u(k-1)]'](/sites/default/files/tex_cache/540fd351d970ef14744bcace885cef4b.png)
Далее (18.2) будем интерпретировать как СЛАУ относительно неизвестных, являющихся координатами вектора  Как известно из алгебры [33], необходимым и достаточным условием разрешимости СЛАУ является представление столбца свободных членов
Как известно из алгебры [33], необходимым и достаточным условием разрешимости СЛАУ является представление столбца свободных членов ![[\bar s]_{\mu}](/sites/default/files/tex_cache/072740c1875cc18d8ed6bde1fe82e92b.png) в виде линейной комбинации линейно независимых столбцов матрицы
в виде линейной комбинации линейно независимых столбцов матрицы 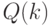 системы (18.2).
системы (18.2).
Поскольку для любого 
![[A^k}_{\mu}=[A^{k_{min}}A^{k-k_{min}}]_{\mu}=[A^{k_{min}}]_{\mu} A^{k-k_{min}}=[0]](/sites/default/files/tex_cache/1ce4cacb58268001ae69dfb2a2efe5b2.png)
то
![Q(k)=[[0], \dots, [0], A^{k_{min}-1}B, \dots, B]_{\mu}](/sites/default/files/tex_cache/f0f1e0be2e7b87d876c71908bc27cdd6.png) |
( 18.3) |
Таким образом, вектор ![[\bar s]_{\mu}](/sites/default/files/tex_cache/072740c1875cc18d8ed6bde1fe82e92b.png) является линейной комбинацией линейно независимых столбцов матрицы (18.3) или, что то же самое, линейно независимых столбцов матрицы
является линейной комбинацией линейно независимых столбцов матрицы (18.3) или, что то же самое, линейно независимых столбцов матрицы  .
.
Следствие 1. Мощность множества всех различных синхросостояний ЛА, заданного над полем 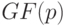 , равна величине
, равна величине  .
.
Заметим, что нулевое обобщенное синхросостояние всегда входит во множество всех синхросостояний ЛА, поскольку при подаче нулевой входной последовательности длины  обобщенно синхронизируемый ЛА переходит в ОС
обобщенно синхронизируемый ЛА переходит в ОС ![[0]_{\mu}](/sites/default/files/tex_cache/8b0f482a487d6c11e7754db12bc04c80.png) .
.
Следствие 2. Если ![[B]_{\mu} \ne [0]](/sites/default/files/tex_cache/271563c25ce5b08e66ab0aaa3430d7a1.png) , то обобщенно синхронизируемый ЛА имеет ненулевое обобщенное синхросостояние .
, то обобщенно синхронизируемый ЛА имеет ненулевое обобщенное синхросостояние .
Это вытекает из того, что если ![[B]_{\mu} \ne [0]](/sites/default/files/tex_cache/271563c25ce5b08e66ab0aaa3430d7a1.png) , то
, то ![\rank [A^{k_{min}-1}B, \dots, B]_{\mu} \ge 1](/sites/default/files/tex_cache/931b67dbb337be456e940e6868b84c24.png) , но тогда
, но тогда 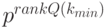 для любого р.
для любого р.
Что касается определения множества всех обобщенных синхросостояний, то, как это следует из теоремы 18.1, оно сводится к нахождению линейного подпространства, порожденного базисом матрицы 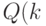 ).
).
Теорема 18.2. Пусть  - минимальная ОСП, а
- минимальная ОСП, а  - произвольная ОСП длины
- произвольная ОСП длины  , переводящая ЛА в одно и то же синхросостояние, и пусть
, переводящая ЛА в одно и то же синхросостояние, и пусть 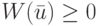 для любого входного символа этого ЛА. Тогда
для любого входного символа этого ЛА. Тогда 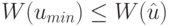 .
.
Доказательство. Предположим, что ОСП 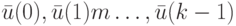 , где
, где  переводит ЛА в обобщенное синхросостояние
переводит ЛА в обобщенное синхросостояние  . Это означает, что
. Это означает, что
![[A^{k-1}B]_{\mu}\bar u(0) + \dots, +[B]_{\mu}\bar u(k-1)=[\bar s]_{\mu}](/sites/default/files/tex_cache/d513971867ec494eed4fd83479121463.png)
Учитывая, что в силу обобщенной синхронизируемости для всех  справедливо равенство
справедливо равенство ![[A^k]_{\mu}=[0]](/sites/default/files/tex_cache/ed06628d567d48e19352af74d795017d.png) , получаем
, получаем
![[0]+\dots +[0]+[A^{k_{min}-1}B]_{\mu}\bar u(k-k_{min})+ \dots +[B]_{\mu} \bar u(k-1)=[\bar s]_{\mu}](/sites/default/files/tex_cache/551d12c971dab64f290d08f1de78d5ea.png)
где слагаемые, содержащие  при
при  , равны [0]. Из полученного равенства следует, что ОСП
, равны [0]. Из полученного равенства следует, что ОСП 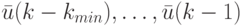 длины
длины  переводит ЛА в обобщенное синхросостояние
переводит ЛА в обобщенное синхросостояние  . В силу неотрицательности весовой функции
. В силу неотрицательности весовой функции 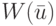 отсюда следует утверждение теоремы.
отсюда следует утверждение теоремы.
Из этой теоремы вытекает следующий вывод: если весовая функция 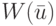 является неотрицательной, то минимальную по весу ОСП рассматриваемого обобщенно синхронизируемого ЛА следует искать среди ОСП минимальной длины.
является неотрицательной, то минимальную по весу ОСП рассматриваемого обобщенно синхронизируемого ЛА следует искать среди ОСП минимальной длины.
В случае, когда весовая функция 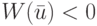 по крайней мере для одного входного символа ЛА, сформулированная в начале этого раздела задача имеет решение только тогда, когда длина искомой ОСП предполагается заранее заданной. Легко показать, что если на длину ОСП ограничений не накладывать, то для этого ЛА можно построить ОСП, вес которой будет меньше любого наперед заданного отрицательного числа.
по крайней мере для одного входного символа ЛА, сформулированная в начале этого раздела задача имеет решение только тогда, когда длина искомой ОСП предполагается заранее заданной. Легко показать, что если на длину ОСП ограничений не накладывать, то для этого ЛА можно построить ОСП, вес которой будет меньше любого наперед заданного отрицательного числа.
Далее предполагается, что весовая функция 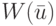 является неотрицательной и матрица
является неотрицательной и матрица 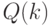 в СЛАУ (18.2), обозначаемая далее как
в СЛАУ (18.2), обозначаемая далее как  , соответствует
, соответствует 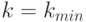 .
.
Вернемся теперь к рассматриваемой задаче. Множество всех ОСП, переводящих ЛА в обобщенное состояние ![[\bar s]_{min}](/sites/default/files/tex_cache/08b64eacaf553bd149b20b449ba86bb1.png) , как это следует из сказанного выше, должно удовлетворять равенству
, как это следует из сказанного выше, должно удовлетворять равенству
![D \hat u=[\br s]_{\mu}](/sites/default/files/tex_cache/6956c956967315a949bb58428e04f836.png)
Здесь вектор-столбец ![\hat u=[u_1(0), \dots, u_l(0), \dots, u_1(k_{min}), \dots, u_l(k_{min})]'](/sites/default/files/tex_cache/8dceb68254784a95812037f62b0b467a.png) . В соответствии с формулировкой задачи искомое решение должно доставлять минимум весовой функции
. В соответствии с формулировкой задачи искомое решение должно доставлять минимум весовой функции 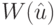 . Учитывая, что переменные
. Учитывая, что переменные 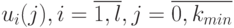 по смыслу задачи являются целыми неотрицательными числами, не превосходящими характеристику
по смыслу задачи являются целыми неотрицательными числами, не превосходящими характеристику  поля
поля 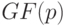 , рассматриваемую задачу можно описать в следующем виде:
, рассматриваемую задачу можно описать в следующем виде:
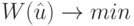 |
( 18.4) |
![D\hat u=[\bar s]_{\mu},\\
0 \le u_i(j) \le p-1, 1 \le I \le l, 0 \le j \le k_{min}](/sites/default/files/tex_cache/7caf3d4a063a0d375651cee438c139a7.png) |
( 18.5) |
Условимся для упрощения обозначений координаты вектора  считать перенумерованными сверху вниз натуральными числами от 1 до
считать перенумерованными сверху вниз натуральными числами от 1 до  . Тогда последнее неравенство примет вид
. Тогда последнее неравенство примет вид
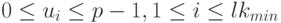 |
( 18.6) |
Сформулированная задача относится к классу задач математического программирования. Скажем более точно: она представляет собой задачу целочисленного программирования [35] с линейными ограничениями (18.5).
Перепишем систему ограничений (18.5) в виде системы сравнений
![Q\hat u=[\bar s]_{\mu} mod p](/sites/default/files/tex_cache/883a51b805034563ca6bd2f7e9c47ad9.png) |
( 18.7) |
Как известно, сравнение 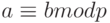 эквивалентно равенству
эквивалентно равенству 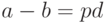 для некоторого целого
для некоторого целого  . Поэтому (18.7) эквивалентна СЛАУ в целых числах:
. Поэтому (18.7) эквивалентна СЛАУ в целых числах:
![Q\hat u=[\bar s]_{\mu}+p\bar d](/sites/default/files/tex_cache/82ba0766d66632967f2d409c0bd3b4e0.png)
где  - вектор-столбец, число координат которого равно числу уравнений в системе (18.7). Таким образом, поставленная задача эквивалентна следующей задаче целочисленного программирования:
- вектор-столбец, число координат которого равно числу уравнений в системе (18.7). Таким образом, поставленная задача эквивалентна следующей задаче целочисленного программирования:
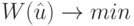 |
( 18.8) |
![Q\hat u=[\hat s]_{\mu}+p\bar d](/sites/default/files/tex_cache/e64b1ab273c2a85df42dc1749cd9a629.png) |
( 18.9) |
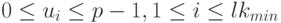 |
( 18.10) |
Заметим, что из (18.9) нетрудно установить диапазон изменения координат вектора  :
:
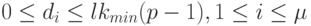
Подведя итоги изложенного, сформулируем следующее утверждение.
Теорема 18.3. Задача построения ОСП минимального веса, переводящей обобщенно синхронизируемый ЛА в заданное обобщенное синхросостояние , всегда может быть сведена к задаче целочисленного программирования с линейными ограничениями.
В настоящее время известен ряд методов решения задач целочисленного программирования [35], в том числе метод сечения, метод разветвленного поиска и оценки и др. Остановимся кратко на том, как может быть адаптирован последний из названных методов для исследуемой нами задачи, поскольку ее специфика позволяет такую адаптацию осуществлять эффективно.
Напомним кратко идею метода разветвленного поиска посредством разделения и оценки, относящегося к группе методов ветвей и границ, широко применяемых в целочисленном программировании
Предположим, что поставлена следующая задача:

где  - некоторое конечное множество целочисленных векторов. Используя верхние оценки для координат вектора
- некоторое конечное множество целочисленных векторов. Используя верхние оценки для координат вектора  , можно с помощью известных методов [28] свести задачу к двоичной. Поэтому далее будем считать, что
, можно с помощью известных методов [28] свести задачу к двоичной. Поэтому далее будем считать, что  есть множество двоичных векторов.
есть множество двоичных векторов.
Используя дискретность множества  , представим его в форме некоторого разветвления. Вершине нулевого уровня, т. е. корню ветвления, соответствует все множество
, представим его в форме некоторого разветвления. Вершине нулевого уровня, т. е. корню ветвления, соответствует все множество  Для построения вершины уровня 1 выберем некоторую переменную
Для построения вершины уровня 1 выберем некоторую переменную  . Этот уровень содержит две вершины, которые соответствуют следующим подмножествам
. Этот уровень содержит две вершины, которые соответствуют следующим подмножествам  : подмножество векторов
: подмножество векторов  для которых
для которых 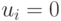 , и подмножество
, и подмножество 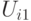 , для которых
, для которых 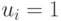 . Понятно, что эти два подмножества образуют разбиение множества
. Понятно, что эти два подмножества образуют разбиение множества  . Будем говорить, что множество
. Будем говорить, что множество  разделено относительно переменных
разделено относительно переменных  . Аналогично, для построения уровня 2 выберем вторую переменную
. Аналогично, для построения уровня 2 выберем вторую переменную  и разделим каждое из полученных на предыдущем этапе подмножеств относительно переменной
и разделим каждое из полученных на предыдущем этапе подмножеств относительно переменной 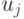 . Таким образом, на уровне 2 получим четыре подмножества: подмножество векторов
. Таким образом, на уровне 2 получим четыре подмножества: подмножество векторов  , для которых
, для которых 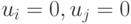 , подмножество векторов
, подмножество векторов 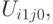 для которых
для которых 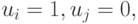 подмножество векторов
подмножество векторов  для которых
для которых 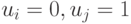 , и подмножество векторов
, и подмножество векторов 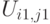 , для которых
, для которых 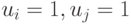 . Аналогичным образом строятся уровни
. Аналогичным образом строятся уровни  , где
, где  - число переменных задач. Каждой вершине построенного дерева соответствует конкретный двоичный вектор из
- число переменных задач. Каждой вершине построенного дерева соответствует конкретный двоичный вектор из  .
.
Перейдем теперь к понятию оценки. Предположим, что для каждой вершины 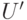 разветвления удалось получить оценку снизу для лучшего решения из множества
разветвления удалось получить оценку снизу для лучшего решения из множества 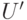 :
:

Функцию  будем называть далее функцией оценки. Построим шаг за шагом, начиная с уровня 0, разветвления множества
будем называть далее функцией оценки. Построим шаг за шагом, начиная с уровня 0, разветвления множества  . Пусть для некоторого допустимого вектора
. Пусть для некоторого допустимого вектора  известно значение
известно значение 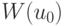 . Предположим, что для некоторой вершины
. Предположим, что для некоторой вершины 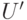 построенного разветвления имеет оценку
построенного разветвления имеет оценку
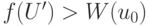
Следовательно, по определению  множество
множество 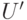 не содержит оптимального решения задачи. Это позволяет избежать исследования всех вершин разветвления, следующего за
не содержит оптимального решения задачи. Это позволяет избежать исследования всех вершин разветвления, следующего за 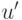 . Используя данный принцип, можно значительно уменьшить перебор элементов допустимого множества, что весьма существенно при большом числе переменных.
. Используя данный принцип, можно значительно уменьшить перебор элементов допустимого множества, что весьма существенно при большом числе переменных.
Заметим, что выбор множества, которое необходимо разделить на очередном этапе, и выбор переменной для разделения в общем случае произволен. Вместе с тем осуществлять такой выбор в каждом конкретном случае необходимо с учетом специфики задачи. Для получения оценок весовой функции часто решается соответствующая непрерывная задача линейного программирования, что является достаточно трудоемким этапом. Тот факт, что при  все коэффициенты, кроме свободных членов в ограничениях для
все коэффициенты, кроме свободных членов в ограничениях для 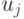 , равны 0 или 1, существенно облегчает решение соответствующих задач. Этот случай часто встречается на практике, поскольку ЛА над полем
, равны 0 или 1, существенно облегчает решение соответствующих задач. Этот случай часто встречается на практике, поскольку ЛА над полем 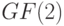 является адекватной моделью различных широко распространенных на практике цифровых устройств. Ниже будет показано, что специфика конкретной задачи позволяет иногда избежать этого этапа, вычисляя функции оценки из других соображений.
является адекватной моделью различных широко распространенных на практике цифровых устройств. Ниже будет показано, что специфика конкретной задачи позволяет иногда избежать этого этапа, вычисляя функции оценки из других соображений.
