Эксперименты по распознаванию неисправностей линейных автоматов
В процессе эксплуатации в цифровых устройствах могут возникнуть различные неисправности. Для обеспечения правильного функционирования этих устройств необходимо проводить их проверку с целью обнаружения возможных неисправностей. Один из способов обнаружения неисправностей заключается в прерывании режима штатной работы устройства и подачи на него специально построенной входной последовательности, называемой тестом. Тест должен обладать следующим свойством: реакция проверяемых устройств на него должна быть различной в зависимости от того, является ли это устройство исправным или содержит неисправность. Следовательно, процесс обнаружения неисправностей представляет собой эксперимент, проводимый над устройством.
Эта лекция посвящена проблеме обнаружения неисправностей в цифровых системах, описываемых моделями линейных автоматов. Ранее известные методы построения тестов для ЛА, описанные в работах [2], [27], содержали жесткие требования, касающиеся как наличия информации о начальном состоянии, так и схемной реализации. Заметим, что эти требования почти никогда не выполняются.
Предлагаемые ниже методы не требуют выполнения упомянутых жестких ограничений и являются менее трудоемкими. Далее предполагается, что в ЛА могут возникать неисправности, приводящие к изменению его характеристических матриц, но не увеличивающие числа его состояний и не выводящие исходное устройство из класса ЛА.
Предполагается также, что неисправность, возникнув в ЛА в некоторый момент, сохраняется в нем и во все последующие моменты времени. Последнее означает, что из рассмотрения исключаются только сбои и перемежающиеся неисправности, которые представляют собой кратковременные самоустраняющиеся неисправности одного и того же типа, появляющиеся в устройстве через некоторые не обязательно равные промежутки времени. Что же касается "неисчезающих" неисправностей, то рассматриваемое разнообразие их видов предельно широко. В самом деле, любые из встречающихся на практике неисправностей, например, типа константных, перепутывания связей, коротких замыканий, изменения реализуемой вентилем функции и т. п., в конечном счете, если они являются существенными, приводят только к изменениям характеристических матриц ЛА.
Ниже рассматривается следующая задача. Пусть задан ЛА и некоторая его неисправная модификация из множества допустимых неисправных модификаций. Требуется построить такую входную последовательность (тест), которая эту неисправность обнаруживает.
Входную последовательность назовем тестом, обнаруживающим заданную неисправность, если независимо от начальных состояний исправного ЛА и его неисправной модификации их входные реакции на эту последовательность различны.
Построенные предложенными ниже методами тесты используются для проведения экспериментов по распознаванию (обнаружению) неисправностей. Тесты подаются на вход ЛА, фиксируется реакция проверяемого устройства на этот тест и по этой реакции делается заключение об исправности или неисправности устройства.
Синтез тестов для стационарных линейных автоматов
Напомним вначале некоторые понятия, которые понадобятся в дальнейшем.
Говорят, что ЛА  имеет конечную память глубины
имеет конечную память глубины  , если в любой момент времени
, если в любой момент времени  выход
выход 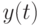 однозначно определяется входом в этот же момент и предыдущими
однозначно определяется входом в этот же момент и предыдущими  входами и
входами и  выходами, т. е. для всех
выходами, т. е. для всех  справедливо соотношение
справедливо соотношение
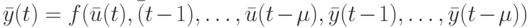
Содержательно это означает, что реакция такого ЛА в произвольный момент времени может быть предсказана только на основе знания входной последовательности и соответствующей реакции ЛА в предшествующие  моментов времени.
моментов времени.
Из теории ЛА известно [19], что каждый ЛА имеет конечную память глубины  , где
, где  (
(  - размерность ЛА).
- размерность ЛА).
Говорят, что ЛА  является
является  - определенным, если его выход
- определенным, если его выход 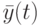 в любой момент времени
в любой момент времени  зависит лишь от предыдущих
зависит лишь от предыдущих  входов, т. е. справедливо соотношение
входов, т. е. справедливо соотношение
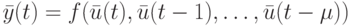
Перейдем теперь к описанию методов построения тестов. Пусть 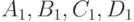 - характеристические матрицы ЛА
- характеристические матрицы ЛА 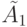 , являющегося неисправной модификацией исходного ЛА
, являющегося неисправной модификацией исходного ЛА  .
.
Рассмотрим случай, когда как исходный ЛА  , так и неисправный ЛА
, так и неисправный ЛА 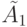 являются
являются  -определенными, однако значения параметра
-определенными, однако значения параметра  для них необязательно совпадают. Пусть
для них необязательно совпадают. Пусть 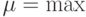 (
( 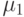 ,
, 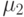 ), где
), где 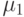 и
и 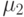 - значения параметра
- значения параметра  для ЛА
для ЛА  и
и 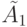 соответственно. В [19] доказано, что необходимым и достаточным условием
соответственно. В [19] доказано, что необходимым и достаточным условием  -определенности ЛА является выполнение соотношения
-определенности ЛА является выполнение соотношения ![CA^{\mu}=[0]](/sites/default/files/tex_cache/a58e889ca05211f8663c6741604f817f.png) . Отсюда следует, что
. Отсюда следует, что ![CA^k=[0]](/sites/default/files/tex_cache/117e2a600551c79f9ae9a049730c016a.png) и
и ![C_1A_1^k=[0]](/sites/default/files/tex_cache/eb7c2a93898670287179d5278f3d4ba3.png) для всех
для всех 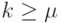 .
.
Если на исправный и неисправный ЛА подана одна и та же входная последовательность 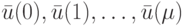 , то с учетом только что приведенных равенств и формулы (1.4) полной реакции ЛА независимо от начальных состояний автоматов
, то с учетом только что приведенных равенств и формулы (1.4) полной реакции ЛА независимо от начальных состояний автоматов  и
и 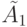 соответствующие реакции имеют вид
соответствующие реакции имеют вид
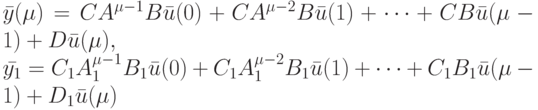
Произведя вычитание, получим
![\bar y(\mu)- \bar {y_1}(\mu)=[CA^{\mu -1}B-C_1A_1^{\mu -1}B_1]\bar u(0)+ \dots +[D-D_1]\bar u(\mu)](/sites/default/files/tex_cache/253de2d18bc95dfca6bcf38e0138da9c.png) |
( 14.1) |
Понятно, что заданная неисправность будет обнаружена входной последовательностью (тестом) 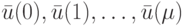 , если и только если реакции
, если и только если реакции 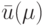 и
и 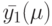 различаются, т. е.
различаются, т. е. ![\bar y(\mu)-\bar {y_1}(\mu) \ne [0]](/sites/default/files/tex_cache/01b0875bc7e120a024a96229a1592899.png) .
.
Соотношение (14.1) будем рассматривать как СЛАУ относительно неизвестных, являющихся координатами вектора
![u =[u_1(0),\dots, u_l(0),\dots, u_1(\mu),\dots, u_l(\mu)]](/sites/default/files/tex_cache/4272e26ee35ee561ee7263d0c919cca0.png) |
( 14.2) |
и на ее основе организуем процедуру построения теста. Обозначим через 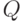 матрицу системы (14.1); тогда (14.1) перепишется в виде
матрицу системы (14.1); тогда (14.1) перепишется в виде
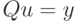 |
( 14.3) |
где  - некоторый
- некоторый  -мерный ненулевой вектор.
-мерный ненулевой вектор.
Обозначим через  множество всех тестов, обнаруживающих заданную неисправность. Для поиска множества
множество всех тестов, обнаруживающих заданную неисправность. Для поиска множества  необходимо варьировать правую часть системы (14.3) и при каждой конкретной правой части находить решение системы, если оно существует.
необходимо варьировать правую часть системы (14.3) и при каждой конкретной правой части находить решение системы, если оно существует.
Легко сообразить, что число всевозможных правых частей системы (14.3) равно величине 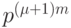 , которая даже при сравнительно небольших значениях параметров
, которая даже при сравнительно небольших значениях параметров  ,
,  и
и  достаточно велика. По этой причине предлагаемый метод довольно трудоемок и мы рассмотрим другой, более эффективный метод.
достаточно велика. По этой причине предлагаемый метод довольно трудоемок и мы рассмотрим другой, более эффективный метод.
Суть его состоит в том, что вместо неоднородной системы (14.3) будет рассматриваться соответствующая ей однородная система
![Qu=[0]](/sites/default/files/tex_cache/f19026e50678527a191096973f4033a6.png) |
( 14.4) |
множество решений которой обозначим через 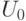 . Если
. Если  - множество всевозможных векторов вида (14.2), то очевидно, что множество
- множество всевозможных векторов вида (14.2), то очевидно, что множество 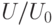 является искомым множеством
является искомым множеством  тестов. Таким образом, при такой организации построения тестов все свелось к решению единственной однородной системы уравнений.
тестов. Таким образом, при такой организации построения тестов все свелось к решению единственной однородной системы уравнений.
Пусть ранг матрицы  равен
равен  . Если
. Если 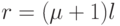 , то из алгебры известно, что нулевое решение будет единственным решением однородной системы (2.4), а при
, то из алгебры известно, что нулевое решение будет единственным решением однородной системы (2.4), а при 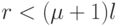 система имеет ненулевые решения, метод поиска которых известен.
система имеет ненулевые решения, метод поиска которых известен.
Проиллюстрируем предложенный метод на примере. Пусть ЛА над полем 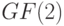 задан следующими характеристическими матрицами (
задан следующими характеристическими матрицами ( 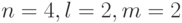 ):
):
![A=
\left [
\begin {matrix}
0&0&0&0\\
1&0&0&0\\
1&1&0&0\\
1&1&1&0
\end {matrix}
\right ],\\
B=
\left [
\begin {matrix}
1&1\\
1&1\\
1&1\\
1&1
\end {matrix}
\right ],\\
C=
\left [
\begin {matrix}
1&1&0&0\\
1&0&0&0
\end {matrix}
\right ],\\
D=
\left [
\begin {matrix}
1&1\\
1&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/5410ebaeb8bdadfe557843e8d4e6cca9.png)
Пусть неисправный автомат задан матрицами
![A_1=
\left [
\begin {matrix}
1&1&1&1\\
1&1&1&1\\
1&0&0&0\\
1&0&0&0\\
\end {matrix}
\right ],\\
B_1=B,\\
C_1=
\left [
\begin {matrix}
1&1&0&0\\
0&0&1&1
\end {matrix}
\right ],\\
D_1=D](/sites/default/files/tex_cache/e22d4ffa4d59fd5c4179eedf0ad1d6bf.png)
Легко проверить, что ![CA^2 = [0]](/sites/default/files/tex_cache/9f5ef04e8af9cdbf0bab115a2b34d592.png) и
и ![CA_1^2 = [0]](/sites/default/files/tex_cache/50eba14051d72ae054d92af5cac3eb19.png) , т. е. оба ЛА являются
, т. е. оба ЛА являются  -определенными (
-определенными ( 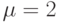 ).
).
По формуле полной реакции имеем следующие результаты:
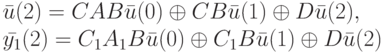
Отсюда получаем однородную линейную систему вида (14.4):
![[CAB \oplus C_1A_1B]\bar u(0) \oplus [CB \oplus C_1B]\bar u(1)=[0]](/sites/default/files/tex_cache/88aa0fbaafdf8253825bafee33d4f0bf.png)
Выполнив соответствующие вычисления, придем к следующей однородной системе уравнений в координатной форме:
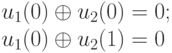
Легко проверить, что ранг матрицы последней системы 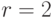 , т. е. он меньше числа неизвестных (
, т. е. он меньше числа неизвестных (  . Отсюда следует, что система имеет ненулевое решение. Считая, например, переменные
. Отсюда следует, что система имеет ненулевое решение. Считая, например, переменные 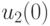 и
и 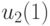 свободными, выразим через них оставшиеся переменные
свободными, выразим через них оставшиеся переменные
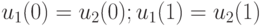 |
( 14.5) |
Отметим, что в рассматриваемой системе переменные 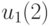 и
и 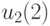 отсутствуют в силу специфики самой системы, т. е. выступают здесь в роли фиктивных переменных. Из сказанного вытекает, что решениями этой однородной системы являются всевозможные значения
отсутствуют в силу специфики самой системы, т. е. выступают здесь в роли фиктивных переменных. Из сказанного вытекает, что решениями этой однородной системы являются всевозможные значения 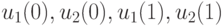 , удовлетворяющие соотношениям (14.5), а также произвольные значения переменных
, удовлетворяющие соотношениям (14.5), а также произвольные значения переменных 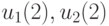 .
.
Зная множество 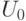 решений рассмотренной однородной системы, построим множество
решений рассмотренной однородной системы, построим множество  всех тестов, обнаруживающих заданную неисправность, как дополнение множества
всех тестов, обнаруживающих заданную неисправность, как дополнение множества 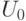 до множества всех
до множества всех 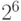 штук двоичных входных наборов
штук двоичных входных наборов ![[u_1(0), u_2(0), u_1(1), u_1(2), u_1(2), u_2(2)]](/sites/default/files/tex_cache/c98d19e50bf80b863133f97bf505c639.png) длины 6. Таким образом, искомое множество
длины 6. Таким образом, искомое множество  составляют всевозможные двоичные входные наборы указанного типа, у которых
составляют всевозможные двоичные входные наборы указанного типа, у которых  и
и  .
.
Обратимся теперь к методу построения тестов для синхронизируемых автоматов. В соответствии с приведенным ранее критерием синхронизируемости для любого синхронизируемого ЛА существует такое целое число  , что
, что ![A^k = [0]](/sites/default/files/tex_cache/38fb7b921d66368535fff295f1f60522.png) , но тогда справедливо и равенство
, но тогда справедливо и равенство ![CA^k = [0]](/sites/default/files/tex_cache/f6e5745b215fa06a62d78f910506c140.png) при любой матрице
при любой матрице  . Отсюда вытекает справедливость следующего утверждения.
. Отсюда вытекает справедливость следующего утверждения.
Теорема 14.1. Каждый синхронизируемый ЛА является одновременно и  -определенным.
-определенным.
Понятно, что эта теорема обосновывает возможности применения описанного выше метода построения тестов к синхронизируемым ЛА.
Предложенный метод построения тестов предполагает, что неисправные ЛА должны сохранять свойства  -определенности или синхронизируемости. Заметим, что это требование не является слишком ограничительным. Так, оно заведомо выполняется, если возникающие в автомате неисправности сказываются только на характеристических матрицах
-определенности или синхронизируемости. Заметим, что это требование не является слишком ограничительным. Так, оно заведомо выполняется, если возникающие в автомате неисправности сказываются только на характеристических матрицах 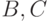 и
и  . Однако не всякое изменение матрицы
. Однако не всякое изменение матрицы  указанные свойства будет сохранять.
указанные свойства будет сохранять.
Перейдем теперь к описанию метода построения тестов для произвольного ЛА, а не обязательно  -определенного либо синхронизируемого. Этот метод базируется на том факте, что любой ЛА является автоматом с конечной памятью.
-определенного либо синхронизируемого. Этот метод базируется на том факте, что любой ЛА является автоматом с конечной памятью.
Предположим, что исправный (неисправный) ЛА имеет глубину памяти 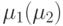 и пусть
и пусть  ). Из теории ЛА известно [19], что функции выходов ЛА
). Из теории ЛА известно [19], что функции выходов ЛА  и
и 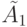 соответственно можно представить в виде:
соответственно можно представить в виде:
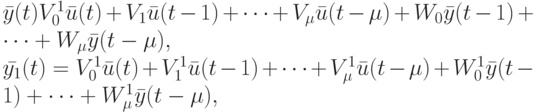 |
( 14.6) |
где 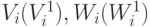 - матрицы соответствующей размерности. Способ приведения функции выхода ЛА к виду (14.6) описан в [19], и мы не будем здесь на нем останавливаться.
- матрицы соответствующей размерности. Способ приведения функции выхода ЛА к виду (14.6) описан в [19], и мы не будем здесь на нем останавливаться.
Очевидно, что входная последовательность 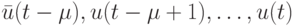 является минимальным по длине тестом, если выходные реакции исправного и неисправного автоматов для всех
является минимальным по длине тестом, если выходные реакции исправного и неисправного автоматов для всех 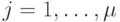 совпадают, т. е.
совпадают, т. е.  , а на последнем такте
, а на последнем такте  . С учетом сказанного, произведя вычитание выражений в (14.6), получим
. С учетом сказанного, произведя вычитание выражений в (14.6), получим
![\bar y (t)- \bar y_1(t)=[V_0-V_0^1]\bar (t) + \dots + [V_{\mu}-V_{\mu}^1] \bar u (t- \mu)+ {W_0 - W_0^1]+ \dots +[W_{\mu} - W_{\mu}^1 \bar y(t-\mu)](/sites/default/files/tex_cache/f4a44820d4463de203566029e7ee36ad.png) |
( 14.7) |
Приравняв выражение (14.7) некоторому ненулевому вектору  , мы получим СЛАУ относительно неизвестных, являющихся координатами вектора
, мы получим СЛАУ относительно неизвестных, являющихся координатами вектора
![u=[u_1(t- \mu), \dots, u_1(t- \mu), \dots, u_1(t), \dots, u_1(t)]'](/sites/default/files/tex_cache/a091a6fb94052b092dfd95698fe5770a.png)
Если через  обозначим матрицу полученной СЛАУ, то в этом обозначении она примет вид
обозначим матрицу полученной СЛАУ, то в этом обозначении она примет вид
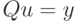
Заметим, что все сказанное выше относительно поиска решений системы (14.3) остается справедливым и для последней системы. Таким образом, построение множества всех тестов для произвольных ЛА, так же как для  -определенных и синхронизируемых ЛА, сводится к решению системы линейных уравнений.
-определенных и синхронизируемых ЛА, сводится к решению системы линейных уравнений.
Проиллюстрируем предложенный метод на примере ЛА над полем  с характеристическими матрицами
с характеристическими матрицами
![A=
\left [
\begin {matrix}
0&1&0&0\\
1&1&0&0\\
0&0&0&1\\
0&1&0&1
\end {matrix}
\right ],\\
B=
\left [
\begin {matrix}
1\\
1\\
1\\
0
\end {matrix}
\right ],\\
C=
\left [
\begin {matrix}
0&1&0&1
\end {matrix}
\right ],
D=[1]](/sites/default/files/tex_cache/2d68f1953c7134d2da718c227dec76ff.png)
Найдем представление функции выхода этого ЛА в виде (14.6). Поскольку минимальный многочлен матрицы  есть
есть 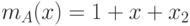 , получаем
, получаем

Тогда, используя формулы полной реакции ЛА и только что полученное равенство, вычислим
![y(2)=CA^2 \bar s (0)+CABu(0)+CBu(1)+Du(0)=\\
=C\bar s(0)+CA\bar s(0)+CABu(0)+CBu(1)+Du(1)=\\
=[y(0)+Du(0)]+[y(1)+CBu(0)+Du(1)]+CABu(0)+CBu(1)+Du(1).](/sites/default/files/tex_cache/5731ce6123862df7743a252e6b3b8bca.png)
После преобразований получаем
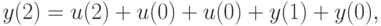
откуда для любого 
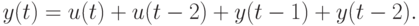
Пусть неисправный ЛА задан следующими характеристическими матрицами:
![A_1=A, B_1=B, C_1=[1 0 1 0], D_1=D.](/sites/default/files/tex_cache/400560922c4613ccba71ac716f1b098d.png)
Проведя аналогичные вычисления для неисправного ЛА, получим
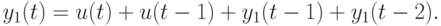
Упоминавшаяся выше СЛАУ для нашего примера примет вид
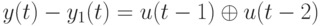
Понятно, что для получения множества всех тестов, обнаруживающих заданную неисправность, необходимо найти все решения СЛАУ
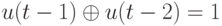
Отсюда получаем, что
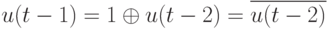
Таким образом, множество всех искомых тестов составляют такие тройки двоичных наборов 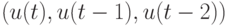 , у которых
, у которых  может иметь произвольное значение, а величины
может иметь произвольное значение, а величины 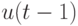 и
и 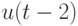 должны быть инверсными.
должны быть инверсными.
Отметим следующий важный факт: предложенный метод строит тест длины 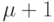 , где
, где 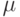 - глубина памяти ЛА. Поскольку, как известно,
- глубина памяти ЛА. Поскольку, как известно,  , где
, где  - размерность ЛА, такой метод дает возможность строить достаточно короткие по длине тесты.
- размерность ЛА, такой метод дает возможность строить достаточно короткие по длине тесты.
