Числовые характеристики зависимости
Ковариация двух случайных величин
Мы знаем, что для независимых случайных величин с конечными вторыми моментами дисперсия их суммы равна сумме их дисперсий. В общем случае дисперсия суммы равна
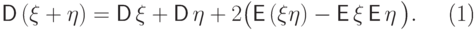 |
( 18) |
Величина  равняется
нулю,
если случайные величины
равняется
нулю,
если случайные величины  и
и  независимы
(свойство (E7) математического ожидания).
С другой стороны, из равенства ее нулю вовсе не следует независимость,
как показывают примеры 50 и 51.
Эту величину используют как "индикатор наличия зависимости" между
двумя случайными величинами.
независимы
(свойство (E7) математического ожидания).
С другой стороны, из равенства ее нулю вовсе не следует независимость,
как показывают примеры 50 и 51.
Эту величину используют как "индикатор наличия зависимости" между
двумя случайными величинами.
Определение 39.
Ковариацией  случайных величин
случайных величин  и
и  называется число
называется число 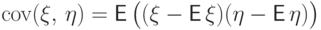 .
.
Свойство 18.
Справедливы равенства: 
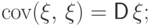

 .
.
Непосредственным возведением суммы в квадрат проверяется следующее свойство.
Свойство 19. Дисперсия суммы нескольких случайных величин вычисляется по любой из следующих формул:
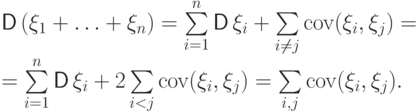
Обсудим достоинства и недостатки ковариации, как величины, характеризующей зависимость двух случайных величин.
Если ковариация  отлична
от нуля, то величины
отлична
от нуля, то величины  и
и  зависимы.
Чтобы судить о наличии зависимости согласно любому из определений
независимости,
требуется знать совместное распределение пары
зависимы.
Чтобы судить о наличии зависимости согласно любому из определений
независимости,
требуется знать совместное распределение пары  и
и  .
Но найти совместное распределение часто бывает
сложнее, чем посчитать математическое ожидание произведения
.
Но найти совместное распределение часто бывает
сложнее, чем посчитать математическое ожидание произведения  и
и  . Если нам повезет, и математическое
ожидание
. Если нам повезет, и математическое
ожидание 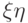 не будет равняться произведению их математических
ожиданий,
мы установим зависимость
не будет равняться произведению их математических
ожиданий,
мы установим зависимость  и
и  не находя
их совместного распределения. Это очень хорошо.
не находя
их совместного распределения. Это очень хорошо.
Пример 65.
Покажем, что с помощью ковариации можно судить о зависимости даже тогда, когда
для вычисления совместного распределения недостаточно данных.
Пусть  и
и  - независимые случайные величины
и
дисперсия
- независимые случайные величины
и
дисперсия  отлична от нуля.
Покажем, что
отлична от нуля.
Покажем, что  и
и  зависимы:
зависимы:

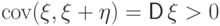 .
Следовательно,
.
Следовательно,  и
и  зависимы.
зависимы.Упражнение.
Доказать, что  и
и  независимы, если
независимы, если 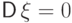 .
.
Величина  не является
"безразмерной": если
не является
"безразмерной": если  - объем газа
в сосуде, а
- объем газа
в сосуде, а  - давление этого газа, то
ковариация измеряется в
- давление этого газа, то
ковариация измеряется в 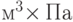 .
Иначе говоря,
при умножении
.
Иначе говоря,
при умножении  или
или  на 100 ковариация
тоже увеличится в 100 раз. Но от умножения на 100 величины
не стали "более зависимыми", так что большое значение ковариации
не означает более сильной зависимости. Это очень плохо.
на 100 ковариация
тоже увеличится в 100 раз. Но от умножения на 100 величины
не стали "более зависимыми", так что большое значение ковариации
не означает более сильной зависимости. Это очень плохо.
Нужно как-то нормировать ковариацию, получив из нее "безразмерную" величину, абсолютное значение которой:
- не менялось бы при умножении случайных величин на число;
- свидетельствовало бы о "силе зависимости" случайных величин.
Замечание Говоря о "силе" зависимости между
случайными величинами, мы имеем в виду следующее. Самая сильная зависимость
-
функциональная, а из функциональных - линейная зависимость, когда  п.н. Бывают гораздо более слабые зависимости. Так, если
по последовательности независимых случайных величин
п.н. Бывают гораздо более слабые зависимости. Так, если
по последовательности независимых случайных величин 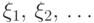 построить величины
построить величины 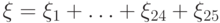 и
и  , то эти величины
зависимы, но очень "слабо": через единственное общее слагаемое
, то эти величины
зависимы, но очень "слабо": через единственное общее слагаемое  .
Сильно ли зависимы
число гербов в первых
.
Сильно ли зависимы
число гербов в первых 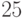 подбрасываниях монеты и число гербов
в испытаниях с
подбрасываниях монеты и число гербов
в испытаниях с 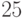 -го по
-го по 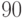 -е?
-е?
Итак, следующая величина есть всего лишь ковариация, нормированная нужным образом.

