Элементарная теория вероятностей
Дискретное пространство элементарных исходов
Пространство элементарных исходов назовем дискретным,
если множество  конечно или счетно:
конечно или счетно: 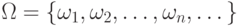 .
.
Так, эксперименты из примеров 1, 2, 3, 5, 6 и 7 (но не 4) приводят к дискретным пространствам элементарных исходов.
Замечание
Множество счетно, если существует взаимно-однозначное соответствие
между этим множеством и множеством всех натуральных чисел. Счетными
множествами являются множество 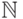 натуральных чисел, множество
натуральных чисел, множество 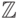 целых чисел, множество
целых чисел, множество  рациональных
чисел, множество четных чисел
и т.д. Множество конечно, если оно состоит из конечного числа элементов.
рациональных
чисел, множество четных чисел
и т.д. Множество конечно, если оно состоит из конечного числа элементов.
Событием на таком пространстве удобно считать любое подмножество  .
.
Чтобы определить вероятность любого события на таком пространстве, присвоим вероятность каждому элементарному исходу в отдельности, т.е. снабдим вероятностями мельчайшие "кирпичики" --- элементарные исходы, из которых составляется любое событие. Вероятность каждого события найдем как сумму вероятностей входящих в него элементарных исходов.
Определение 3.
Сопоставим каждому элементарному исходу 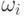 число
число ![p_{i}\in [0,1]](/sites/default/files/tex_cache/2921ce720f170ca941b5f8782413edbd.png) так, чтобы
так, чтобы  .
Число
.
Число 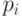 назовем вероятностью элементарного исхода
назовем вероятностью элементарного исхода 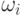 .
Вероятностью события
.
Вероятностью события  называется число
называется число
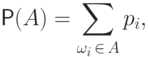
 .
В случае
.
В случае 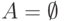 положим
положим 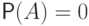 .
.Замечание Позднее, познакомившись с аксиоматикой теории вероятностей, мы зададим вероятности событий непосредственно, а не через вероятности элементарных исходов. Ведь сложением вероятностей элементарных исходов можно получить лишь вероятность события, состоящего не более чем из счетного числа элементарных исходов (иначе само понятие суммирования не определено). Но на дискретном пространстве элементарных исходов всегда возможно определить вероятности событий согласно определению 3.
Пример 10. В эксперименте из примера 5 монета подбрасывается до первого выпадения герба. Присвоим элементарным исходам следующие вероятности:
![\begin{matrix}
\omega_{i}: & \textit{г},\; & \textit{рг},\; & \textit{ррг},\;
& \textit{рррг},\; & \ldots \\[.5mm]
& \; & \; & \;
& \; & \\[2mm]
p_{i}: & \;\frac12\,, & \;\frac14\,, &
\;\frac18\,, & \;\frac{1}{16}\,, & \ldots
\end{matrix}](/sites/default/files/tex_cache/a2fa05ab2bc4e0f13188e75cdde382d2.png)
Проверим, что сумма вероятностей элементарных исходов равна единице: по формуле суммы бесконечной убывающей геометрической прогрессии,
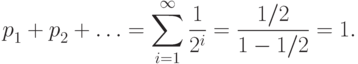
 (герб
выпал при броске с четным номером) равна:
(герб
выпал при броске с четным номером) равна: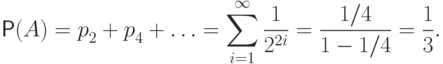
Заданные выше вероятности соответствуют, как мы увидим в дальнейшем,
подбрасыванию правильной монеты. Можно было задать вероятности как-нибудь
иначе: например, 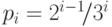 . Такие
вероятности отвечали бы
бросанию утяжеленной монеты, герб на которой выпадает в среднем
в одном случае из трех.
. Такие
вероятности отвечали бы
бросанию утяжеленной монеты, герб на которой выпадает в среднем
в одном случае из трех.
Пример 11.
На том же самом множестве 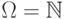 зададим вероятности так:
зададим вероятности так: 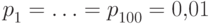 ,
,  для
для 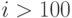 .
.
Пример 12.
На том же 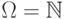 положим
положим 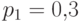 ,
, 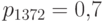 , остальные
, остальные 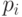 равны нулю.
Читатель легко найдет вероятности событий
равны нулю.
Читатель легко найдет вероятности событий  и
и 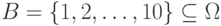 .
.
Пример 13.
Пусть теперь  - множество целых
неотрицательных чисел.
Положим
- множество целых
неотрицательных чисел.
Положим

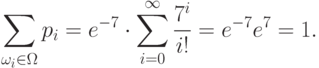
Внимательный читатель уже заметил, что если множество  счетно,
но не конечно, присвоить всем элементарным исходам одну и ту же вероятность
нельзя.
Для конечного же множества
счетно,
но не конечно, присвоить всем элементарным исходам одну и ту же вероятность
нельзя.
Для конечного же множества  всегда возможно задать
одинаковые вероятности
исходов, что мы сейчас и сделаем.
всегда возможно задать
одинаковые вероятности
исходов, что мы сейчас и сделаем.
Классическое определение вероятности. Частным, но часто встречающимся в жизни случаем дискретного вероятностного пространства является классическая вероятностная схема.
Предположим, что мы имеем дело с пространством элементарных
исходов, состоящим из конечного числа элементов:  и из каких-то соображений
можем считать элементарные исходы равновозможными.
Равновозможность возникает обычно из-за симметрии
в эксперименте (симметричная монета, хорошо перемешанная колода карт,
правильная игральная кость, отсутствие оснований предпочесть один результат
эксперимента
другому).
и из каких-то соображений
можем считать элементарные исходы равновозможными.
Равновозможность возникает обычно из-за симметрии
в эксперименте (симметричная монета, хорошо перемешанная колода карт,
правильная игральная кость, отсутствие оснований предпочесть один результат
эксперимента
другому).
Говорят, что эксперимент описывается классической
вероятностной моделью,
если пространство его элементарных исходов состоит из конечного
числа равновозможных исходов.
Тогда вероятность любого элементарного исхода равна  .
Если событие
.
Если событие 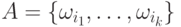 состоит из
состоит из  элементарных исходов, то вероятность этого события
равна отношению
элементарных исходов, то вероятность этого события
равна отношению  :
:
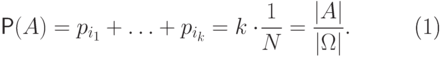 |
( 2.1) |
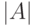 обозначено число элементов конечного множества
обозначено число элементов конечного множества  .
.Формулу 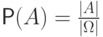 называют классическим определением вероятности
и читают так:
"вероятность события
называют классическим определением вероятности
и читают так:
"вероятность события  равна отношению числа исходов,
благоприятствующих этому событию, к общему числу равновозможных
исходов".
равна отношению числа исходов,
благоприятствующих этому событию, к общему числу равновозможных
исходов".
Итак, вычисление вероятности в классической схеме сводится к подсчету общего числа исходов (шансов) и числа исходов, благоприятствующих событию. Число шансов вычисляют с помощью формул комбинаторики.
Рассмотрим стандартные урновые схемы: из  шаров выбирают
шаров выбирают  шаров.
Будем исходить из предположения о том, что появление любого шара
равновозможно. Тогда три схемы: схема выбора с возвращением и с учетом порядка,
выбора без возвращения и с учетом порядка, а также
выбора без возвращения и без учета порядка, описываются классической
вероятностной моделью. Общее число равновозможных элементарных исходов в этих
схемах равно соответственно
шаров.
Будем исходить из предположения о том, что появление любого шара
равновозможно. Тогда три схемы: схема выбора с возвращением и с учетом порядка,
выбора без возвращения и с учетом порядка, а также
выбора без возвращения и без учета порядка, описываются классической
вероятностной моделью. Общее число равновозможных элементарных исходов в этих
схемах равно соответственно 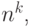
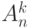 и
и 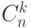 .
.
Как показывает следующий пример, последняя схема - схема выбора с возвращением и без учета порядка - имеет неравновозможные исходы. Поэтому классическое определение вероятности для нее не применимо.

