Лекция 7: Нелинейное программирование. Классификация методов нелинейного программирования. Классический метод определения условного экстремума. Метод множителей Лагранжа
1. Понятие нелинейного программирования
В большинстве инженерных задач построение математической модели не удается свести к задаче линейного программирования.
Математические модели в задачах проектирования реальных объектов или технологических процессов должны отражать реальные протекающие в них физические и, как правило, нелинейные процессы. Переменные этих объектов или процессов связанны между собой физическими нелинейными законами, такими, как законы сохранения массы или энергии. Они ограничены предельными диапазонами, обеспечивающими физическую реализуемость данного объекта или процесса. В результате, большинство задач математического программирования, которые встречаются в научно-исследовательских проектах и в задачах проектирования – это задачи нелинейного программирования (НП).
Пусть в математической модели проектируемого объекта или процесса
непрерывная функция  представляет собой
функцию цели (функцию качества),
представляет собой
функцию цели (функцию качества),
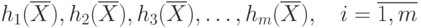

![\overline{X}=[x_1, x_2, x_3, \ldots, x_n], \;
\overline{X} \in E^n](/sites/default/files/tex_cache/3d1a2bad0fdd673053e37147a11ac7ec.png) - вектор параметров проектируемого объекта,
процесса или системы, оптимальные значения которых должны быть найдены.
- вектор параметров проектируемого объекта,
процесса или системы, оптимальные значения которых должны быть найдены.Тогда задача нелинейного программирования может быть сформулирована следующим образом:
найти вектор ![\overline{X}=[x_1, x_2, x_3, \ldots, x_n], \;
\overline{X} \in E^n](/sites/default/files/tex_cache/3d1a2bad0fdd673053e37147a11ac7ec.png) , доставляющий минимум (максимум) целевой
функции
, доставляющий минимум (максимум) целевой
функции  при m линейных и
(или) нелинейных ограничений в виде равенств
при m линейных и
(или) нелинейных ограничений в виде равенств

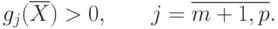
В течение последних двух десятилетий из нелинейного программирования выделились самостоятельные разделы:
- выпуклое программирование,
- квадратичное программирование,
- целочисленное программирование,
- стохастическое программирование,
- динамическое программирование и др.
Задачи выпуклого программирования – это задачи, в которых определяется минимум выпуклой функции (или максимум вогнутой), заданной на выпуклом замкнутом множестве. Эти задачи среди задач нелинейного программирования наиболее изучены.
Среди задач выпуклого программирования более подробно изучены задачи квадратичного программирования. В этих задачах целевая функция – квадратична, а ограничения – линейны.
В задачах целочисленного программирования неизвестные параметры могут принимать только целочисленные значения.
В задачах стохастического программирования в целевой функции или в функциях ограничений содержатся случайные величины, которые подчиняются законам теории вероятностей.
В задачах динамического программирования ограничения содержат как параметр время и при этом описываются дифференциальными уравнениями. Процесс нахождения решений в задачах динамического программирования является многоэтапным.
