Сортировка (часть 2)
Выбор
В сортировке посредством выбора основная идея состоит в том, чтобы
идти по шагам 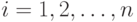 , находя
, находя  -е
наибольшее (наименьшее)
имя и помещая его на его место на
-е
наибольшее (наименьшее)
имя и помещая его на его место на  -ом шаге. Простейшая форма
сортировки выбором представлена алгоритмом 15.1:
-ом шаге. Простейшая форма
сортировки выбором представлена алгоритмом 15.1:  -е наибольшее
имя
находится очевидным способом просмотром оставшихся
-е наибольшее
имя
находится очевидным способом просмотром оставшихся 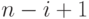 имен. Число
сравнений имен на
имен. Число
сравнений имен на  -ом шаге равно
-ом шаге равно 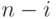 , что
приводит к общему числу
сравнений имен
, что
приводит к общему числу
сравнений имен 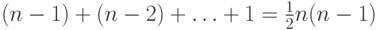 независимо от входа, поэтому ясно, что это не очень хороший способ
сортировки.
независимо от входа, поэтому ясно, что это не очень хороший способ
сортировки.
Несмотря на неэффективность алгоритма 15.1, идея выбора может привести
и к эффективному алгоритму сортировки. Весь вопрос в том, чтобы найти
более эффективный метод определения  -го наибольшего имени, чего
можно добиться, используя механизм турнира с выбыванием. Суть его
такова: сравниваются
-го наибольшего имени, чего
можно добиться, используя механизм турнира с выбыванием. Суть его
такова: сравниваются  , затем сравниваются "победители" (то есть большие
имена) этих
сравнений и т.д.; эта процедура для
, затем сравниваются "победители" (то есть большие
имена) этих
сравнений и т.д.; эта процедура для 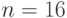 показана на рис. 15.1.
Заметим, что для определения наибольшего имени этот процесс требует
показана на рис. 15.1.
Заметим, что для определения наибольшего имени этот процесс требует 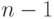 сравнений имен; но, определив наибольшее имя, мы обладаем большим
объемом информации о втором по величине (в порядке убывания) имени: оно
должно быть одним из тех, которые "потерпели поражение" от
наибольшего имени. Таким образом, второе по величине имя теперь можно определить,
заменяя наибольшее имя на
сравнений имен; но, определив наибольшее имя, мы обладаем большим
объемом информации о втором по величине (в порядке убывания) имени: оно
должно быть одним из тех, которые "потерпели поражение" от
наибольшего имени. Таким образом, второе по величине имя теперь можно определить,
заменяя наибольшее имя на  и вновь осуществляя сравнение
вдоль пути от наибольшего имени к корню. На рис. 15.2 эта процедура показана для
дерева из рис. 15.1.
и вновь осуществляя сравнение
вдоль пути от наибольшего имени к корню. На рис. 15.2 эта процедура показана для
дерева из рис. 15.1.
Идея турнира с выбыванием прослеживается при сортировке весьма отчетливо,
если имена образуют пирамиду. Пирамида
- это полностью сбалансированное бинарное дерево высоты  , в котором все листья находятся на
расстоянии
, в котором все листья находятся на
расстоянии  или
или 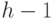 от корня и все потомки узла
меньше его самого; кроме того, в нем все листья уровня
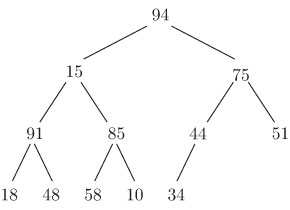
максимально смещены влево. На рис. 15.3 показано множество имен, организованных
в виде пирамиды. Чтобы получить удобное линейное представление дерева, пирамиду
можно хранить по уровням в одномерном массиве: сыновья имени из
от корня и все потомки узла
меньше его самого; кроме того, в нем все листья уровня
максимально смещены влево. На рис. 15.3 показано множество имен, организованных
в виде пирамиды. Чтобы получить удобное линейное представление дерева, пирамиду
можно хранить по уровням в одномерном массиве: сыновья имени из  -ой позиции есть имена в позициях
-ой позиции есть имена в позициях 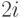 и
и 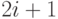 . Таким образом, пирамида, представленная на рисунке 15.3, принимает
вид
. Таким образом, пирамида, представленная на рисунке 15.3, принимает
вид
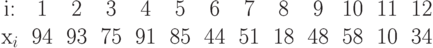
Заметим, что в пирамиде наибольшее имя должно находиться в корне и, таким
образом, всегда в первой позиции массива, представляющего пирамиду. Обмен
местами первого имени с  -м помещает наибольшее имя в его
правильную позицию, но нарушает свойство
пирамидальности в первых
-м помещает наибольшее имя в его
правильную позицию, но нарушает свойство
пирамидальности в первых 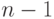 именах. Если мы можем сначала
построить пирамиду, а затем эффективно
восстановить ее, то все в порядке, так как тогда можно производить сортировку
следующим образом:
построить пирамиду из
именах. Если мы можем сначала
построить пирамиду, а затем эффективно
восстановить ее, то все в порядке, так как тогда можно производить сортировку
следующим образом:
построить пирамиду из  ,
,
Это общее описание пирамидальной сортировки.
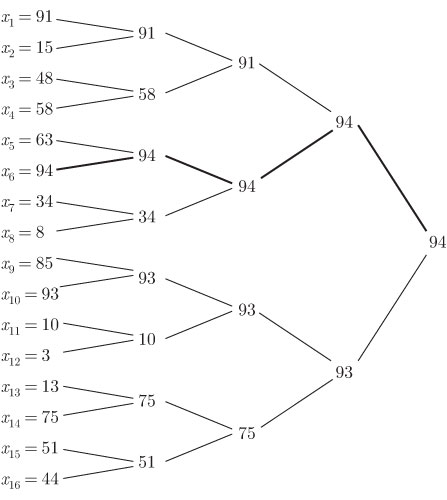
Рис. 15.1. Использование турнира с выбыванием для отыскания наибольшего имени.Путь наибольшего имени показан жирной линией
Процедура RESTORE  восстановления пирамиды из
последовательности
восстановления пирамиды из
последовательности 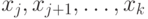 в предположении, что
все поддеревья суть пирамиды, такова:
в предположении, что
все поддеревья суть пирамиды, такова:
Переписывая это итеративным способом и дополняя деталями, мы получим алгоритм 15.2.
Распределяющая сортировка
Обсуждаемый здесь алгоритм сортировки отличается от рассматривавшихся до
сих пор тем, что он основан не на сравнениях между именами, а на представлении
имен. Мы полагаем, что каждое из имен  имеет
вид
имеет
вид
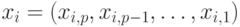

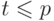 имеем
имеем  для
для  и
и  . Для простоты будем считать, что
. Для простоты будем считать, что 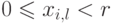 , и поэтому имена можно рассматривать как
целые, представленные по основанию
, и поэтому имена можно рассматривать как
целые, представленные по основанию  , так что каждое имя имеет
, так что каждое имя имеет 
 -ичных цифр. Более короткие имена дополняются
нулями.
-ичных цифр. Более короткие имена дополняются
нулями.Цифровая распределяющая сортировка
Цифровая распределяющая сортировка основана на наблюдении, что если имена
уже отсортированы по младшим разрядами 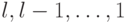 , то их
можно полностью отсортировать, сортируя только по старшим разрядам
, то их
можно полностью отсортировать, сортируя только по старшим разрядам 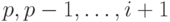 при условии, что сортировка осуществляется таким
образом, чтобы не нарушить
относительный порядок имен с одинаковыми цифрами в старших разрядах. Заметим,
что к самой таблице обращаются по правилу "первым включается – первым
исключается", и поэтому лучшим способом представления являются очереди. В
частности, предположим, что с каждым ключом
при условии, что сортировка осуществляется таким
образом, чтобы не нарушить
относительный порядок имен с одинаковыми цифрами в старших разрядах. Заметим,
что к самой таблице обращаются по правилу "первым включается – первым
исключается", и поэтому лучшим способом представления являются очереди. В
частности, предположим, что с каждым ключом  ассоциируется
поле связи
ассоциируется
поле связи 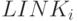 ; тогда эти поля связи можно использовать для
сцепления всех имен в таблице вместе
во входную очередь
; тогда эти поля связи можно использовать для
сцепления всех имен в таблице вместе
во входную очередь  . При помощи полей связи можно также сцеплять
имена в очереди
. При помощи полей связи можно также сцеплять
имена в очереди 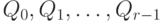 , используемые для
представления стопок. После того как имена распределены по
стопкам, очереди, представляющие эти стопки, связываются вместе для получения
вновь таблицы
, используемые для
представления стопок. После того как имена распределены по
стопкам, очереди, представляющие эти стопки, связываются вместе для получения
вновь таблицы  . Алгоритм 15.4. представляет эту процедуру в
общих чертах (очереди описаны в
"Алгоритмы на абстрактных структурах данных"
).
В результате применения алгоритма очередь
. Алгоритм 15.4. представляет эту процедуру в
общих чертах (очереди описаны в
"Алгоритмы на абстрактных структурах данных"
).
В результате применения алгоритма очередь  будет
содержать имена в порядке возрастания; то есть имена будут связаны в порядке
возрастания полями связи, начиная с головы очереди
будет
содержать имена в порядке возрастания; то есть имена будут связаны в порядке
возрастания полями связи, начиная с головы очереди  .
.

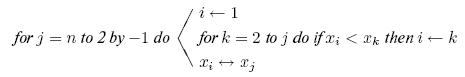



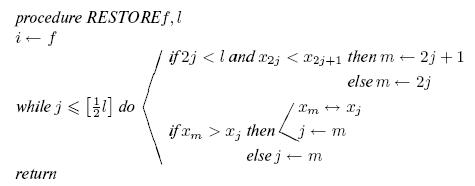
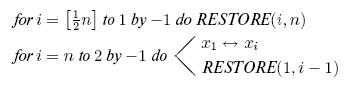
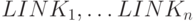 для формирования
для формирования 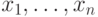 во входную
во входную 