Рекурсия

5.3. Рекурсивный алгоритм

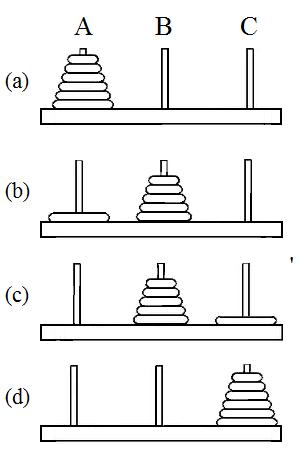
Рассмотрим задачу о ханойской башне. Эту задачу придумал Эдуард Люка в XIX веке. Задача заключается в следующем. Имеется три стержня — левый, средний и правый. На левом стержне находятся n дисков, диаметры которых попарно различны (рис. 5.2 (а)). Диски упорядочены по размеру диаметра, сверху лежит наименьший, снизу — наибольший. Требуется перенести диски с левого стержня на правый, используя средний стержень как вспомогательный. Переносить можно только по одному диску, при этом нельзя класть диск большего диаметра на диск меньшего диаметра.

Рис. 5.2. Ханойская башня

Очевидно, что для того чтобы перенести нижний диск на правый стержень, нужно предварительно перенести башню, состоящую из n – 1 дисков, с левого стержня на средний стержень (рис. 5.2 (b)). После того, как нижний диск окажется на правом стержне (рис. 5.2 (c)), останется перенести башню со среднего стержня на правый стержень (рис. 5.2 (d)). Нетрудно показать, что оптимальное решение задачи с n дисками состоит из 2ⁿ – 1 перемещений дисков.

class predicates
    hanoi: (positive N, string Откуда, string ВспСтерж, string Куда).
clauses
    hanoi(0, _, _, _):- !.
    hanoi(N, A, B, C):-
        % перенос с A на B с помощью С
        hanoi(N - 1, A, C, B),
        writef("Перенести диск % с % на %\n", N, A, C),
        % перенос с B на C с помощью A
        hanoi(N - 1, B, A, C).

    run():-
        hanoi(3, "A", "B", "C"),
        _ = readLine().

Упражнения

1. Определите на множестве кубиков отношение "не ниже", которое является рефлексивно-транзитивным замыканием отношения наверху. Пара кубиков принадлежит отношению наверху, если первый из них стоит на втором.
2. Сгенерируйте подмножество целых чисел от числа m до числа n включительно с шагом s
   • по возрастанию;
   • по убыванию.
3. По заданному натуральному числу n найдите два соседних элемента последовательности Фибоначчи с номерами n и n + 1.
4. Вычислите значение n–й частичной суммы разложения функции 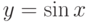в ряд по степеням x в заданной точке.
5. Вычислите с заданной погрешностью значение функции 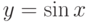в заданной точке с помощью разложения в ряд по степеням x.
6. Для заданного натурального n вычислите значение 1/sin 1 + 1/(sin 1 + sin 2) + … + 1/(sin 1 + … + sin n).
7. По двум точкам, заданным координатами в консоли, постройте соединяющий их "отрезок" в виде набора точек. Отобразите "отрезок" в окне консоли.
8. Для представления неотрицательных целых чисел в виде термов o, s(o), s(s(o)), s(s(s(o))), …, определите операции сложения и умножения, а также функцию вычисления факториала.