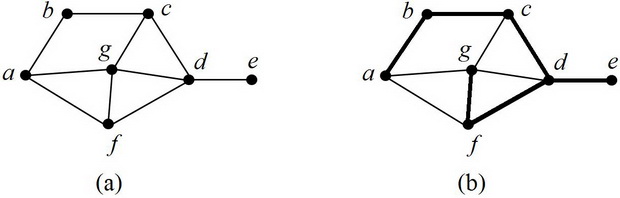Графы

В настоящей главе изучаются основные методы поиска путей на графах — поиск в глубину и поиск в ширину. Рассматривается отношение достижимости на графе. Разбираются некоторые способы поиска кратчайших путей. Генерируется случайный лабиринт, визуализируется проход по нему.

Для представления графа в языке Пролог обычно используются факты. Например, пусть в отдельных фактах хранятся вершины и ребра графа:

node("a").
node("b").
node("c").

arc(1, "a", "b").   % номер ребра, его начало и конец
arc(2, "b", "c").

Тогда предикат, возвращающий элементы матрицы инцидентности, можно определить следующим образом:

incidenceMatrix(Node, Edge, Elem):-
    node(Node), 
    arc(Edge, Node1, Node2),
    getElem(Node, Node1, Node2, Elem).

getElem(Node, Node, _, 1):- !.
getElem(Node, _, Node, -1):- !. % 1 для неориент. графа
getElem(_, _, _, 0).

?- incidenceMatrix(Node, Edge, Elem).

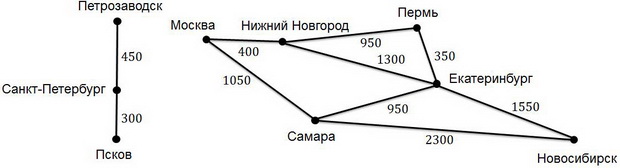
В качестве основного примера в данной главе используется система дорог, которая связывает некоторые города. Эту систему можно изобразить в виде нагруженного графа, вершины которого соответствуют городам, а ребра — соединяющим им дорогам (рис. 8.1).

Рис. 8.1. Граф системы дорог

Граф представляется в виде множества ребер, для хранения которых используются факты:

clauses
arc("Москва", "Нижний Новгород", 400).
arc("Нижний Новгород", "Пермь",  950).
arc("Екатеринбург", "Пермь",  350).
arc("Екатеринбург", "Новосибирск",  1550).
arc("Нижний Новгород", "Екатеринбург", 1300).
arc("Москва", "Самара", 1050).
arc("Самара", "Екатеринбург", 950).
arc("Самара", "Новосибирск", 2300).
arc("Санкт-Петербург", "Петрозаводск", 450).
arc("Санкт-Петербург", "Псков", 300).

В директории Exe проекта следует создать текстовый файл graph.txt и поместить в него данные факты.

8.1. Поиск в глубину

Поиск в глубину является естественным для языка Пролог, он используется машиной вывода Пролога для вычисления целей. Поэтому поиск в глубину путей на графах реализуется в языке Пролог наиболее просто.

Поясним идею поиска в глубину на следующем примере. Рассмотрим граф, изображенный на рис. 8.2 (a).

Рис. 8.2. (a) Связный граф; (b) обход графа в глубину

Пусть ребра графа хранятся в следующем порядке: . Совершим обход графа из вершины . Будем двигаться вперед по ребрам и помечать пройденные вершины до тех пор, пока будут встречаться непомеченные вершины. Когда это станет невозможным, вернемся в последнюю пройденную вершину , для которой существует непомеченная смежная с ней вершина. Далее обход будет совершаться из вершины . Обход продолжается до тех пор, пока остаются непомеченные вершины. Схематично обход графа можно представить следующим образом (рис. 8.2 (b)):

Рис. 8.3. Схематичное изображение обхода графа

В следующих двух программах для нахождения путей используется поиск в глубину. В первой программе используется функциональный стиль, а во второй предикатный. Во второй программе вместе с поиском подсчитывается длина пути. Отношение edge является симметричным замыканием отношения arc. Для хранения пройденного пути используется список. В процессе вычислений вершины записываются в список, как в стек, поэтому к найденному пути применяется операция обращения списка.

class facts - graph
    arc: (string Город1, string Город2, unsigned Расстояние).

class predicates
    depthFirst: (string, string) -> string* nondeterm.
    path: (string, string, string*) -> string* nondeterm.
    edge: (string, string, unsigned) nondeterm (i,o,o).
clauses
    edge(X, Y, Dist):-
        arc(X, Y, Dist);
        arc(Y, X, Dist).

    depthFirst(Start, Goal) = list::reverse(path(Start, Goal, [Start])).

    path(Goal, Goal, Path) = Path:- !.
    path(V, Goal, CurrPath) = path(NextV, Goal, [NextV | CurrPath]):-
        edge(V, NextV, _),
        not(list::isMember(NextV, CurrPath)).

    run():-
        file::consult("graph.txt", graph),
        VertexList = depthFirst("Москва", "Новосибирск"),
            write(string::concatWithDelimiter(VertexList, " -> ")), nl,
        fail;
        _ = readLine().

Предикат concatWithDelimiter соединяет список строк в одну строку, вставляя между ними заданный разделитель.

Для текущей вершины можно не использовать отдельный аргумент (см. выше определение предиката path/3):

    depthFirst(Start, Goal) = list::reverse(path([Start], Goal)).

    path([Goal | Path], Goal) = [Goal | Path].
    path([V | Path], Goal) = path([NextV, V | Path], Goal):-
        edge(V, NextV, _),
        not(NextV in Path).

Упражнение 1. Найдите все пути из Москвы в Новосибирск, проходящие через Пермь^{1Пример приведен для версии 7.5. В версии 7.4 вместо выражения not(A in B) должно быть not(list::isMember(A, B)). Вместо A и B в листингах стоят разные переменные.}.

class facts - graph
    arc: (string, string, unsigned).

class predicates
    depthFirst: (string, string, string* [out], unsigned [out]) 
        nondeterm.
    path: (string, string, string*, string* [out], unsigned, 
        unsigned [out]) nondeterm.
    edge: (string, string, unsigned) nondeterm (i,o,o).
clauses
    edge(X, Y, Dist):-
        arc(X, Y, Dist);
        arc(Y, X, Dist).

    depthFirst(Start, Goal, list::reverse(Path), Dist):-
        path(Start, Goal, [Start], Path, 0, Dist).

    path(Goal, Goal, Path, Path, Dist, Dist):- !.
    path(V, Goal, CurrPath, Path, CurrDist, Dist):-
        edge(V, NextV, D),
        not(NextV in CurrPath),
        path(NextV, Goal, [NextV | CurrPath], Path, CurrDist + D, Dist).

    run():-
        file::consult("graph.txt", graph),
        depthFirst("Москва", "Новосибирск", Path, D),
            write(string::concatWithDelimiter(Path, " -> "), " : ", D), nl,
        fail;
        _ = readLine().

Упражнение 2.

1. Найдите все пути, не превосходящие заданной длины.
2. Найдите все пути от одного пункта до другого, которые содержат не более заданного числа пересадок.