|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Квантовые процессоры на переходах Джозефсона
Введение
Другим перспективным направлением реализации квантовых процессоров является использование явлений сверхпроводимости и макроскопической квантовой интерференции. В лекции 3 мы напомнили вам основные сведения об этих явлениях и рассмотрели свойства переходов Джозефсона (ПД) и сквидов на ПД. Перед изучением данной лекции мы советуем Вам перечитать еще раз лекцию 3, чтобы "освежить" в своей памяти изложенные там знания.
На основе сквидов с наноразмерными ПД строят также кубиты для квантовых вычислений. В данной лекции мы рассмотрим ряд вариантов построения таких кубитов, а также вопрос реализации на таких кубитах квантовых процессоров.
Зарядовые кубиты
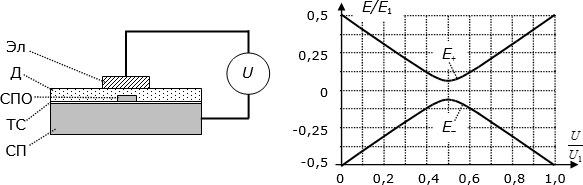
Простейший из сверхпроводящих кубитов на ПД, который называют "зарядовым", показан на
рис.
10.1 слева. Он состоит из относительно массивного сверхпроводника (СП), который называют "берегом" или "резервуаром" (куперовских пар электронов), и расположенного рядом с ним маленького (наноразмерного) электрически изолированного сверхпроводящего островка СПО, который в англоязычной литературе получил название "the single Cooper-pair box" (SCPB или SCB). Островок СПО соединен с резервуаром СП через очень тонкий туннельный слой ТС, образующий переход Джозефсона между двумя сверхпроводниками. Близ сверхпроводящего островка СПО формируют электрод Эл, отделенный от островка толстым слоем диэлектрика Д. Внешнее устройство  используют или для контроля состояния островка (тогда это устройство для измерения потенциала), или для управления этим состоянием (тогда это генератор напряжения).
используют или для контроля состояния островка (тогда это устройство для измерения потенциала), или для управления этим состоянием (тогда это генератор напряжения).
В состоянии сверхпроводимости на островке может находиться лишь целое число избыточных куперовских пар электронов ( ). Каждому числу пар
). Каждому числу пар  отвечает своя "зарядовая" энергия
отвечает своя "зарядовая" энергия
 |
( 10.1) |
 – электрический заряд наноостровка,
– электрический заряд наноостровка,  – электрический заряд электрона,
– электрический заряд электрона,  – суммарная емкость сверхпроводящего наноостровка относительно его окружения. Наибольший вклад в
– суммарная емкость сверхпроводящего наноостровка относительно его окружения. Наибольший вклад в  вносит емкость ПД. Удельная электрическая емкость такого туннельного перехода составляет обычно порядка 5*10-14 Ф/мкм2 = 50 фФ/мкм2. В частности, когда
вносит емкость ПД. Удельная электрическая емкость такого туннельного перехода составляет обычно порядка 5*10-14 Ф/мкм2 = 50 фФ/мкм2. В частности, когда 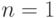 , зарядовая энергия (на одну избыточную куперовскую пару)
, зарядовая энергия (на одну избыточную куперовскую пару)
 |
( 10.2) |
Для зарядовых кубитов важно, чтобы зарядовая энергия (11.2) была больше, чем энергия т.н. "джозефсоновской связи"
 |
( 10.3) |
 – т.н. "квант сопротивления",
– т.н. "квант сопротивления",  – сопротивление туннельного ПД в "нормальном" состоянии (т.е. для обычных, не спаренных электронов проводимости),
– сопротивление туннельного ПД в "нормальном" состоянии (т.е. для обычных, не спаренных электронов проводимости),  – энергия связи куперовской пары. Нередко энергию джозефсоновской связи сокращенно называют "джозефсоновской энергией".
– энергия связи куперовской пары. Нередко энергию джозефсоновской связи сокращенно называют "джозефсоновской энергией".Зарядовая энергия  , как вытекает из (11.1), тем больше, чем меньше площадь туннельного контакта островка СПО с резервуаром СП, в то время как джозефсоновская энергия
, как вытекает из (11.1), тем больше, чем меньше площадь туннельного контакта островка СПО с резервуаром СП, в то время как джозефсоновская энергия  с увеличением этой площади возрастает (так как уменьшается
с увеличением этой площади возрастает (так как уменьшается  ). Именно поэтому условие
). Именно поэтому условие 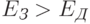 легче выполнить, используя наноразмерные островки.
легче выполнить, используя наноразмерные островки.
Когда на контролирующем электроде Эл поддерживается потенциал  , то в сверхпроводящем островке наводится дополнительный электрический заряд
, то в сверхпроводящем островке наводится дополнительный электрический заряд  , где
, где  – емкость между островком и контролирующим электродом. Этот дополнительный электрический заряд вовсе не обязан быть кратным заряду электрона, так как физически – это результат смещения электронов и куперовских пар в островке относительно положительно заряженных ядер. А это смещение может быть как угодно малым. Индуцированный контролирующим электродом дополнительный заряд придает кубиту дополнительную потенциальную энергию
– емкость между островком и контролирующим электродом. Этот дополнительный электрический заряд вовсе не обязан быть кратным заряду электрона, так как физически – это результат смещения электронов и куперовских пар в островке относительно положительно заряженных ядер. А это смещение может быть как угодно малым. Индуцированный контролирующим электродом дополнительный заряд придает кубиту дополнительную потенциальную энергию
 |
( 10.4) |
Решение стационарного уравнения Шредингера для только что описанной системы показывает, что зарядовый кубит имеет в этом случае два разрешенных значения энергии
 |
( 10.5) |
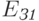 и
и  определяются формулами (11.2) и (11.3).
определяются формулами (11.2) и (11.3).Зависимость разрешенных значений энергии зарядового кубита от потенциала контролирующего электрода показана на
рис.
10.1 справа. Когда потенциал на контролирующем электроде равен нулю, кубит может находиться или в нижнем энергетическом состоянии ( ), которое считают базовым состоянием
), которое считают базовым состоянием 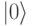 , или в верхнем энергетическом состоянии (
, или в верхнем энергетическом состоянии ( ), которое считают базовым состоянием
), которое считают базовым состоянием 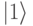 . В базовом состоянии
. В базовом состоянии 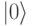 сверхпроводящий островок является электрически нейтральным, а в базовом состоянии
сверхпроводящий островок является электрически нейтральным, а в базовом состоянии 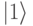 на нем находится одна избыточная куперовская пара.
на нем находится одна избыточная куперовская пара.
Когда потенциал на контролирующем электроде возрастает, энергетическая щель между разрешенными энергетическими состояниями уменьшается, достигая минимума при 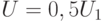 , а потом снова возрастает. При
, а потом снова возрастает. При 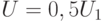 нижний разрешенный уровень энергии
нижний разрешенный уровень энергии  , а верхний
, а верхний  . Переход из одного энергетического состояния в другое происходит здесь с наименьшими затратами энергии. Поэтому "рабочую точку" зарядового кубита чаще всего выбирают именно при
. Переход из одного энергетического состояния в другое происходит здесь с наименьшими затратами энергии. Поэтому "рабочую точку" зарядового кубита чаще всего выбирают именно при 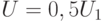 . Исследования показали, что в этой рабочей точке удается достичь также и наибольшего времени сохранения когерентности.
. Исследования показали, что в этой рабочей точке удается достичь также и наибольшего времени сохранения когерентности.
Для манипуляций квантовым состоянием зарядового кубита и для считывания этого состояния сверхпроводящий островок СПО делают продолговатым ( рис. 10.2 слева), например, с размерами 400х50х15 нм, и формируют над ним не один, а два электрода Эл1 и Эл2. Один из них (Эл1) является контролирующим, а второй (Эл2) используется для считывания или для манипуляций состоянием кубита.

Рис. 10.2. Слева – зарядовый кубит с двумя электродами: СП – "массивный" сверхпроводник ("резервуар"); ТС – туннельный слой; СПО – сверхпроводящий островок; Эл1 – контролирующий электрод; Эл2 –управляющий электрод; слой диэлектрика между СПО и электродами для упрощения на рисунке не показан. Справа – "линейка" зарядовых кубитов
В частности, если на управляющий электрод Эл2 подать короткий (продолжительностью порядка 50 пс) импульс отрицательного напряжения с амплитудой  , то из него в сверхпроводящий островок СПО туннельно проникает одна куперовская пара, и зарядовый кубит переходит в базовое состояние
, то из него в сверхпроводящий островок СПО туннельно проникает одна куперовская пара, и зарядовый кубит переходит в базовое состояние 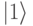 . Если затем на управляющий электрод Эл2 подать короткий импульс положительного напряжения с амплитудой
. Если затем на управляющий электрод Эл2 подать короткий импульс положительного напряжения с амплитудой  , то на него из сверхпроводящего островка НПО туннельно проникает одна куперовская пара, и зарядовый кубит возвращается в базовое состояние
, то на него из сверхпроводящего островка НПО туннельно проникает одна куперовская пара, и зарядовый кубит возвращается в базовое состояние 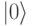 .
.
Если импульс длится дольше, чем требуется для туннелирования куперовской пары, то он служит причиной дальнейшей эволюции волновой функции кубита с переходом в гибридное состояние. В гибридном состоянии куперовская пара электронов находится на островке СПО лишь частично. Это – чисто квантовое явление, совсем невозможное с классической точки зрения. Но эксперименты подтверждают, что это именно так. Оказалось, что, регулируя длительность короткого импульса напряжения на управляющем электроде, можно выполнять над кубитом запланированные квантовые логические операции.
Для считывания состояния зарядового кубита управляющий электрод Эл2 присоединяют ко входу чувствительного измерителя заряда на основе одноелектронного транзистора, позволяющего измерять величину суммарного электрического заряда на сверхпроводящем островке, мало влияя на этот заряд.
Зарядовые кубиты легко объединять в "линейки" и в массивы. На рис. 10.2 справа показана структура линейки зарядовых кубитов. Поскольку кулоновское взаимодействие между электрическими зарядами происходит на довольно больших расстояниях, то зарядовые кубиты в массивах всегда электростатически связаны между собой.
Зарядовые кубиты нормально функционируют лишь при сверхнизких температурах – ниже  . Их основным недостатком является то, что до сих пор не удалось достичь в них достаточно продолжительного времени когерентности. Проведению квантовых вычислений на таких кубитах мешает также и то, что все они довольно сильно связаны электростатическими силами. Выполняя квантовую логическую операцию над одним из кубитов, мы одновременно слегка влияем и на другие, особенно на соседние кубиты.
. Их основным недостатком является то, что до сих пор не удалось достичь в них достаточно продолжительного времени когерентности. Проведению квантовых вычислений на таких кубитах мешает также и то, что все они довольно сильно связаны электростатическими силами. Выполняя квантовую логическую операцию над одним из кубитов, мы одновременно слегка влияем и на другие, особенно на соседние кубиты.
Зато передавать вдоль линейки зарядовых кубитов неизвестное квантовое состояние с одного конца на другой удается неплохо. Поэтому их можно использовать как каналы передачи квантовой информации. Правда, в соответствии с теоремой "о невозможности клонирования квантовых состояний" лишь последний зарядовый кубит в "канале связи" будет в переданном квантовом состоянии, а все предыдущие кубиты переходят в общем случае в другое состояние.