Лекция 6: Элементы теории перевода

Классы атрибутных грамматик и их реализация

В общем виде реализация вычислителей для атрибутных грамматик вызывает значительные трудности. Это связано с тем, что множество значений атрибутов, связанных с данным деревом, приходится вычислять в соответствии с зависимостями атрибутов, которые образуют ориентированный ациклический граф. На практике стараются осуществлять процесс вычисления атрибутов, привязывая его к тому или иному способу обхода дерева. Рассматривают многовизитные, многопроходные и другие атрибутные вычислители. Это, как правило, ведет к ограничению допустимых зависимостей между атрибутами, поддерживаемых вычислителем.

Простейшими подклассами атрибутных грамматик, вычисления всех атрибутов для которых может быть осуществлено одновременно с синтаксическим анализом, являются S -атрибутные и L -атрибутные грамматики. Определение. Атрибутная грамматика называется S - атрибутной, если она содержит только синтезируемые атрибуты.

Нетрудно видеть, что для S -атрибутной грамматики на любом дереве разбора все атрибуты могут быть вычислены за один обход дерева снизу вверх. Таким образом, вычисление атрибутов можно делать параллельно с восходящим синтаксическим анализом, например, LR(1)- анализом.

Пример 5.8. Рассмотрим S -атрибутную грамматику для перевода арифметических выражений в ПОЛИЗ. Здесь атрибут v имеет строковый тип, k - обозначает операцию конкатенации. Правила вывода и семантические правила определяются следующим образом

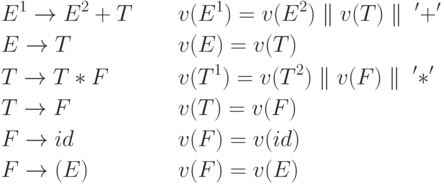
Определение. Атрибутная грамматика называется L - атрибутной, если любой наследуемый атрибут любого символа X_j из правой части каждого правила X₀ -> X₁X₂ ... X_n грамматики зависит только от

1. атрибутов символов X₁, X₂, . . . , X_j-1, находящихся в правиле слева от X_j, и
2. наследуемых атрибутов символа X₀.

Заметим, что каждая S -атрибутная грамматика является L -атрибутной. Все атрибуты на любом дереве для L - атрибутной грамматики могут быть вычислены за один обход дерева сверху-вниз слева-направо. Таким образом, вычисление атрибутов можно осуществлять параллельно с нисходящим синтаксическим анализом, например, LL(1)- анализом или рекурсивным спуском.

В случае рекурсивного спуска в каждой функции, соответствующей нетерминалу, надо определить формальные параметры, передаваемые по значению, для наследуемых атрибутов, и формальные параметры, передаваемые по ссылке, для синтезируемых атрибутов. В качестве примера рассмотрим реализацию атрибутной грамматики из примера 5.5 (нетрудно видеть, что грамматика является L -атрибутной).

void int_part(float * V0, int * P0)
{if (Map[InSym]==Digit)
  { int I=InSym;
    float V2;
    int P2;
    InSym=getInSym();
    int_part(&V2,&P2);
    *V0=I*exp(P2*ln(10))+V2;
    *P0=P2+1;
  }
  else {*V0=0;
        *P0=0;
    }
 }
void fract_part(float * V0, int P0)
{if (Map[InSym]==Digit)
  { int I=InSym;
    float V2;
    int P2=P0+1;
    InSym=getInSym();
    fract_part(&V2,P2);
    *V0=I*exp(-P0*ln(10))+V2;
  }
  else {*V0=0;
    }
}
void number()
{ float V1,V3,V0;
  int P;
    int_part(&V1,&P);
    if (InSym!='.') error();
    fract_part(&V3,1);
    V0=V1+V3;
}

Язык описания атрибутных грамматик

Формализм атрибутных грамматик оказался очень удобным средством для описания семантики языков программирования. Вместе с тем выяснилось, что реализация вычислителей для атрибутных грамматик общего вида сталкивается с большими трудностями. В связи с этим было сделано множество попыток рассматривать те или иные классы атрибутных грамматик, обладающих "хорошими" свойствами. К числу таких свойств относятся прежде всего простота алгоритма проверки атрибутной грамматики на зацикленность и простота алгоритма вычисления атрибутов для атрибутных грамматик данного класса.

Атрибутные грамматики использовались для описания семантики языков программирования и было создано несколько систем автоматизации разработки трансляторов, основанных на формализме атрибутных грамматик. Опыт их использования показал, что "чистый" атрибутный формализм может быть успешно применен для описания семантики языка, но его использование вызывает трудности при создании транслятора. Эти трудности связаны как с самим формализмом, так и с некоторыми технологическими проблемами. К трудностям первого рода можно отнести несоответствие чисто функциональной природы атрибутного вычислителя и связанной с ней неупорядоченностью процесса вычисления атрибутов (что в значительной степени является преимуществом этого формализма) и упорядоченностью элементов программы. Это несоответствие ведет к тому, что приходится идти на искусственные приемы для их сочетания. Технологические трудности связаны с эффективностью трансляторов, полученных с помощью атрибутных систем. Как правило, качество таких трансляторов довольно низко из-за больших расходов памяти, неэффективности искусственных приемов, о которых было сказано выше.

Учитывая это, мы будем вести дальнейшее изложение на языке, сочетающем особенности атрибутного формализма и обычного языка программирования, в котором предполагается наличие операторов, а значит, и возможность управления порядком исполнения операторов. Этот порядок может быть привязан к обходу атрибутированного дерева разбора сверху вниз слева направо. Что касается грамматики входного языка, то мы не будем предполагать принадлежность ее определенному классу (например, LL(1) или LR(1)). Будем считать, что дерево разбора входной программы уже построено как результат синтаксического анализа и атрибутные вычисления осуществляются в результате обхода этого дерева. Таким образом, входная грамматика атрибутного вычислителя может быть даже неоднозначной, что не влияет на процесс атрибутных вычислений.

При записи синтаксиса мы будем использовать расширенную БНФ. Элемент правой части синтаксического правила, заключенный в скобки [ ], может отсутствовать. Элемент правой части синтаксического правила, заключенный в скобки ( ), означает возможность повторения один или более раз. Элемент правой части синтаксического правила, заключенный в скобки [()], означает возможность повторения ноль или более раз. В скобках [ ] или [()] может указываться разделитель конструкций.

Ниже дан синтаксис языка описания атрибутных грамматик. Приведен только синтаксис конструкций, собственно описывающих атрибутные вычисления. Синтаксис обычных выражений и операторов не приводится - он основывается на Си.

Атрибутная грамматика::='ALPHABET'
        ( ОписаниеНетерминала ) ( Правило )
ОписаниеНетерминала::=ИмяНетерминала
            '::' [( ОписаниеАтрибутов / ';')]'.'
ОписаниеАтрибутов::=Тип ( ИмяАтрибута / ',')
Правило::='RULE' Синтаксис 'SEMANTICS' Семантика'.'
Синтаксис::=ИмяНетерминала '::=' ПраваяЧасть
ПраваяЧасть::=[( ЭлементПравойЧасти )]
ЭлементПравойЧасти::=ИмяНетерминала
        | Терминал
        | '(' Нетерминал [ '/' Терминал ] ')'
        | '[' Нетерминал ']'
        | '[(' Нетерминал [ '/' Терминал ] ')]'
Семантика::=[(ЛокальноеОбъявление / ';')]
        [( СемантическоеДействие / ';')]
СемантическоеДействие::=Присваивание
        | [ Метка ] Оператор
Присваивание::=Переменная ':=' Выражение
Переменная::=ЛокальнаяПеременная
      | Атрибут
Атрибут::=ЛокальныйАтрибут
    | ГлобальныйАтрибут
ЛокальныйАтрибут::=ИмяАтрибута '<' Номер '>'
ГлобальныйАтрибут::=ИмяАтрибута '<' Нетерминал '>'
Метка::=Целое ':'
  | Целое 'Е' ':'
  | Целое 'А' ':'
Оператор::=Условный
    | ОператорПроцедуры
    | ЦиклПоМножеству
    | ПростойЦикл
    | ЦиклСУсловиемОкончания

Описание атрибутной грамматики состоит из раздела описания атрибутов и раздела правил. Раздел описания атрибутов определяет состав атрибутов для каждого символа грамматики и тип каждого атрибута. Правила состоят из синтаксической и семантической части. В синтаксической части используется расширенная БНФ. Семантическая часть правила состоит из локальных объявлений и семантических действий. В качестве семантических действий допускаются как атрибутные присваивания, так и составные операторы.

Метка в семантической части правила привязывает выполнение оператора к обходу дерева разбора сверху- вниз слева направо. Конструкция i: оператор означает, что оператор должен быть выполнен сразу после обхода i - й компоненты правой части. Конструкция i E: оператор означает, что оператор должен быть выполнен, только если порождение i -й компоненты правой части пусто. Конструкция i A : оператор означает, что оператор должен быть выполнен после разбора каждого повторения i -й компоненты правой части (имеется в виду конструкция повторения).

Каждое правило может иметь локальные определения (типов и переменных). В формулах используются как атрибуты символов данного правила (локальные атрибуты) и в этом случае соответствующие символы указываются номерами в правиле ( 0 - для символа левой части, 1 - для первого символа правой части, 2 - для второго символа правой части и т.д.), так и атрибуты символов предков левой части правила (глобальные атрибуты). В этом случае соответствующий символ указывается именем нетерминала. Таким образом, на дереве образуются области видимости атрибутов: атрибут символа имеет область видимости, состоящую из правила, в которое символ входит в правую часть, плюс все поддерево, корнем которого является символ, за исключением поддеревьев - потомков того же символа в этом поддереве.

Значение терминального символа доступно через атрибут VAL соответствующего типа.

Пример 5.9. Атрибутная грамматика из примера 5.5 записывается следующим образом:

ALPHABET
Num :: float V.
Int :: float V;
        int P.
Frac :: float V;
        int P.
digit :: int VAL.

RULE
Num ::= Int '.' Frac
SEMANTICS
V<0>=V<1>+V<3>; P<3>=1.

RULE
Int ::= e
SEMANTICS
V<0>=0; P<0>=0.

RULE
Int ::= digit Int
SEMANTICS
V<0>=VAL<1>*10**P<2>+V<2>; P<0>=P<2>+1.

RULE
Frac ::= e
SEMANTICS
V<0>=0.

RULE
Frac ::= digit Frac
SEMANTICS
V<0>=VAL<1>*10**(-P<0>)+V<2>; P<2>=P<0>+1.