Моделирование и анализ параллельных вычислений
2.5.3. Модифицированная каскадная схема
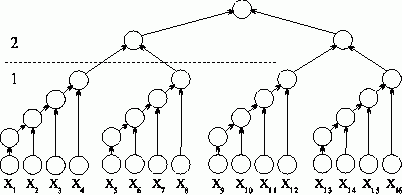
Получение асимптотически ненулевой эффективности может быть обеспечено, например, при использовании модифицированной каскадной схемы (см. [22]). Для упрощения построения оценок можно предположить n=2k, k=2s. Тогда в новом варианте каскадной схемы все вычисления производятся в два последовательно выполняемых этапа суммирования (см. рис. 2.4):
- на первом этапе вычислений все суммируемые значения подразделяются на (n/log2n ) групп, в каждой из которых содержится log2n элементов; далее для каждой группы вычисляется сумма значений при помощи последовательного алгоритма суммирования; вычисления в каждой группе могут выполняться независимо друг от друга (т.е. параллельно – для этого необходимо наличие не менее (n/log2n ) процессоров);
- на втором этапе для полученных (n/log2n) сумм отдельных групп применяется обычная каскадная схема.
Тогда для выполнения первого этапа требуется log2n параллельных операций при использовании p1=(n/log2n) процессоров. Для выполнения второго этапа необходимо
log2(n/log2n)<=log2n
параллельных операций для p2=(n/log2n)/2 процессоров. Как результат, данный способ суммирования характеризуется следующими показателями:
Tp=2log2n, p=(n/log2n).
С учетом полученных оценок показатели ускорения и эффективности модифицированной каскадной схемы определяются соотношениями:
Sp=T1/Tp=(n–1)/2log2n, Ep=T1/pTp=(n–1)/(2(n/log2n)log2n)=(n–1)/2n.
Сравнивая данные оценки с показателями обычной каскадной схемы, можно отметить, что ускорение для предложенного параллельного алгоритма уменьшилось в 2 раза, однако для эффективности нового метода суммирования можно получить асимптотически ненулевую оценку снизу

Можно отметить также, что данные значения показателей достигаются при количестве процессоров, определенном в теореме 5. Кроме того, необходимо подчеркнуть, что, в отличие от обычной каскадной схемы, модифицированный каскадный алгоритм является стоимостно-оптимальным, поскольку стоимость вычислений в этом случае
Cp=pTp=(n/log2n)(2log2n)
является пропорциональной времени выполнения последовательного алгоритма.
2.5.4. Вычисление всех частных сумм
Вернемся к исходной задаче вычисления всех частных сумм последовательности значений и проведем анализ возможных способов последовательной и параллельной организации вычислений. Вычисление всех частных сумм на скалярном компьютере может быть получено при помощи обычного последовательного алгоритма суммирования при том же количестве операций (!)
T1=n.
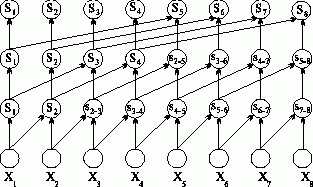
При параллельном исполнении применение каскадной схемы в явном виде не приводит к желаемым результатам; достижение эффективного распараллеливания требует привлечения новых подходов (может быть, даже не имеющих аналогов при последовательном программировании) для разработки новых параллельно-ориентированных алгоритмов решения задач. Так, для рассматриваемой задачи нахождения всех частных сумм алгоритм, обеспечивающий получение результатов за log2n параллельных операций (как и в случае вычисления общей суммы), может состоять в следующем (см. рис. 2.5, а также [22]):
- перед началом вычислений создается копия S вектора суммируемых значений ( S=x );
- далее на каждой итерации суммирования i, 1<=i<=log2n, формируется вспомогательный вектор Q путем сдвига вправо вектора S на 2i-1 позиций (освобождающиеся при сдвиге позиции слева устанавливаются в нулевые значения); итерация алгоритма завершается параллельной операцией суммирования векторов S и Q.
(величины Si-j означают суммы значений от i до j элементов числовой последовательности)
Всего параллельный алгоритм выполняется за log2n параллельных операций сложения. На каждой итерации алгоритма параллельно выполняются n скалярных операций сложения и, таким образом, общее количество скалярных операций определяется величиной
Kпар=nlog2n
(параллельный алгоритм содержит большее (!) количество операций по сравнению с последовательным способом суммирования). Необходимое количество процессоров определяется количеством суммируемых значений ( p=n ).
С учетом полученных соотношений показатели ускорения и эффективности параллельного алгоритма вычисления всех частных сумм оцениваются следующим образом:
Sp=T1/Tp=n/log2n, Ep=T1/pTp=n/(plog2n)=n/(nlog2n)=1/log2n.
Как следует из построенных оценок, эффективность алгоритма также уменьшается при увеличении числа суммируемых значений, и при необходимости повышения величины этого показателя может оказаться полезной модификация алгоритма, как и в случае с обычной каскадной схемой.